For any beginner user, it is truly puzzling why quantities in Abaqus lack units. This often leads to confusion regarding stress units and when entering parameters such as Young’s Modulus, density, and more. This isn’t just an issue with Abaqus; nearly all finite element programs (including Ansys, LS-Dyna, and others) overlook the consideration of unit systems for provided quantities. Thus, it falls upon the user to ensure that the provided numerical values are accompanied by consistent units. To understand how units in Abaqus and how to appropriately select an Abaqus consistent unit system, I recommend reading this post. By the end of the post, the CAE assistant team has provided an Abaqus units table that can be quite helpful.
1. Abaqus units | A Comprehensive Overview of Units in Abaqus
Abaqus has no units built into it except for rotation and angle measures. Therefore, the units chosen must be self-consistent, which means that derived units of the chosen system can be expressed in terms of the fundamental units without conversion factors. Read this useful article in 4 minutes to get enough information about Abaqus units or units in Abaqus.
The different types of units are CGS system units, FPS system units, MKS system units, and SI units.
The CGS units are the centimeter-gram-second system of units. This metric system uses the unit of “centimeter” to denote the distance/length, gram is used as the basic unit to denote mass /weight, and “seconds” is used to denote time.
The FPS units are the foot-pound-second system of units. This metric system uses the foot as the standard unit of length, pound is set as the unit for denoting mass and force. Lastly, the second is used to denote time.
The MKS units are meter, kilogram, and second system of units. This metric system is used to denote the measurement of physical quantities. Here meter is used for denoting length, kilogram is used for denoting mass. It was known for setting the base for the SI units before they were redefined.
The SI unit is the most recent and modern type of metric system used throughout the world. It is often used as the standard unit of measurement. It mainly contains 7 units of measurement which are:
- ampere (symbol: A) – unit of electric current
- kelvin (symbol: K) – unit of temperature
- second (symbol: s) – unit of time
- meter (symbol: m) – unit of length
- kilogram (symbol: kg) – unit of mass
- candela (symbol: cd) – unit of luminous intensity
- mole (symbol: mol) – unit reflecting the amount of a substance
1.1. Abaqus consistent units
Generally, any consistent system of units consists of some fundamental units such as Length (L), Mass (M) or Force (F), and Time (T) as base units and the other units are named derived units, which are formed by powers, products, or quotients of the base units and are potentially unlimited in number.
The International System of Units (SI) is an example of a self-consistent set of units. The fundamental units in the SI system are length in meters (m), mass in kilograms (kg), time in seconds (s), the temperature in degrees Kelvin (K), and electric current in Amperes (A).
Combinations of base and derived units may be used to express other derived units. The definition of derived units is based on fundamental physical relations:
For example, A unit of force in the SI system is called a Newton (N):
Another example is the unit of energy called a Joule (J):
 |
⭐⭐⭐ Abaqus Course | ⏰10 hours Video 👩🎓+1000 Students ♾️ Lifetime Access
✅ Module by Module Training ✅ Standard/Explicit Analyses Tutorial ✅ Subroutines (UMAT) Training … ✅ Python Scripting Lesson & Examples |
1.2. Choosing a suitable Abaqus consistent units
Sometimes the standard units are not convenient to work with. For example, Young’s modulus is frequently specified in terms of MegaPascals (MPa) (or, equivalently, N/mm2), where 1 Pascal = 1 N/m2. In this case, the fundamental units could be tonnes (1 tonne = 1000 kilograms), millimeters, and seconds.
There are numerous different sets of units that can be used when performing FE simulations. The best set of units will depend on the problem; typically, the most accurate results are obtained if the units are chosen such that the values of the input quantities to the FE simulation are close to unity. By having the input quantities close to 1, the influence of round-off errors and truncation errors are reduced.
2. Example of Abaqus units | How to choose the right unit systems for analyses?
Let us see a practical example for choosing appropriate Abaqus units:
We have modeled a fullerene C60 in Abaqus and applied forces (distributed) to its ends (like a tension test). C60 has dimensions in the order of nm (1e-9 m). Our forces are also in nN.
E=1.16 Tera-Pascal = 1.16 e+12 Pa
How we can model this geometry in Abaqus?
What is the Young Modulus unit? What is the mass density unit?
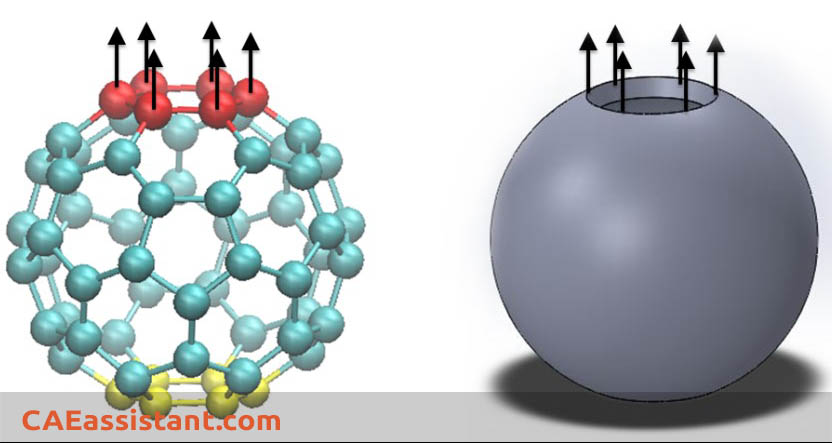
Modeling sub-micron quantities is not possible in Abaqus/CAE since geometric limits are set. It means that you cannot model a sphere of radius 1e-9 in Abaqus/CAE. Besides, if it was possible, due to the influence of round-off errors and truncation errors for very small values, the analysis would stop soon.
Therefore, we need to scale down the model and make the necessary changes in the material properties.
Remember the base units in SI: FLT=Force, Length and Time
For example, we select nN as force base unit, nm as length unit and s as time unit.
It means we will make our geometry saying all dimensions in nm.
Now, for Young Modulus, which is a kind of stress, we have:
So, we must enter Yong Modulus in 10^9 Pa:
We enter 1.16 e+3 as Young Modulus in Abaqus.
Remember that you are doing a numerical calculation in Abaqus, and 3 mm and .003 m are different for a computer; it needs more memory to save and do calculations on .003 than 3.
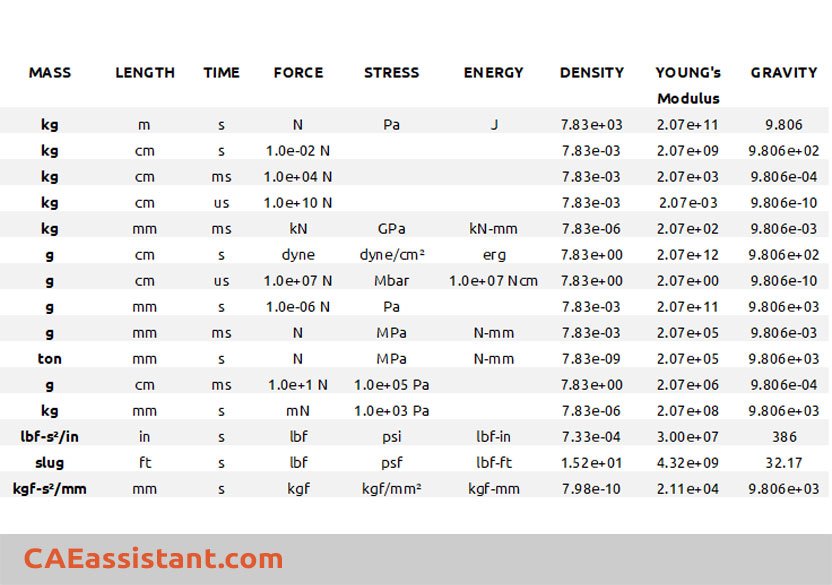
3. Abaqus units table | examples of consistent systems of units
The following table provides examples of consistent systems of units. As points of reference, the mass density and Young’s Modulus of steel are provided in each system of units. “GRAVITY” is the gravitational acceleration. Abaqus units table:
4. Cautions When Using Imperial Units
The naming conventions are not as clear as in the SI system for imperial (American or English) units and they can cause confusion. Frequently, it is not made clear in handbooks whether lb stands for lbm or lbf. You need to check that the values used to make up a consistent set of units.
For example, 1 pound-force (lbf) will give one pound-mass (lbm) an acceleration of g ft/sec2, where g is the value of acceleration due to gravity. If we take pounds-force, feet (ft), and seconds as fundamental units, the derived unit of mass is lbf sec2/ft. Since density is commonly given in handbooks as lbm/in3, it must be converted to lbf sec2/ft4 by
Two other units that cause difficulty are the slug, the mass that will accelerate at 1 ft/sec^2 by 1 lbf, and the poundal, which we define it as the force required to accelerate 1 lbm at 1 ft/sec2. Useful conversions are
1 slug = g x lbm
and
1 lbf = g x poundals
where g is the magnitude of the acceleration due to gravity in ft/sec2.
5. How can I simulate in Abaqus correctly? Is there any tutorial?
In this article, CAE assistant team has attempted to cover all your needs around units in Abaqus. I have listed some main Abaqus Free Tutorials that you may use when simulating an Abaqus project at an advanced level as a graduate student or researcher. You can learn what you want by clicking on that.
I hope you got enough information about Abaqus units and how to calculate Abaqus consistent units. In the below video, you can see the part of this tutorial related to the system of units in Abaqus.
6. Quiz Time!
How can we convert the SI units for specific heat capacity (J/kg-K) and Thermal Conductivity (W/m-K) into consistent units when we model the geometry in mm? In other words, what is the conversion factor for these quantities when we model in mm?
Finally, It would be useful to see Abaqus Documentation to understand how it would be hard to start an Abaqus simulation without any Abaqus tutorial.
Get this post as a PDF file: CAE assistant.com-units-in-abaqus
What is the system of units in ABAQUS?
ABAQUS has no units built into it except for rotation and angle measures. Therefore, the units chosen must be self-consistent, which means that derived units of the chosen system can be expressed in terms of the fundamental units without conversion factors.
The user must apply a system of units that is self-consistent for the simulation to obtain accurate and meaningful results. The choice of units depends on the specific requirements and conventions relevant to the physical quantities involved in the simulation (Units in Abaqus). Respecting self-consistency and the relation between fundamental units and derived units, you can determine any dimension unit you may need in your simulation. So, you need to know the different systems of units in order to define units you may need in your Abaqus simulations (Abaqus Units).
What is the appropriate unit system in Abaqus?
There are numerous different sets of units that can be used when performing FE simulations. The best set of units will depend on the problem; typically, the most accurate results are obtained if the units are chosen such that the values of the input quantities to the FE simulation are close to unity. Having the input quantities close to 1 reduces the influence of round-off errors and truncation errors. For example, modeling a very small dimension is not possible in Abaqus/CAE since geometric limits are set. Besides, if it was possible, due to the influence of round-off errors and truncation errors for very small values, the analysis would stop soon. Therefore, we need to scale down the model and make the necessary changes in the material properties.
What is the unit of density in Abaqus?
Combinations of The fundamental units may be used to express other derived units. Density is the mass of an object divided by its volume. If the user assumes The unit of mass is kilogram and the unit of volume is the cubic meter, Density has the unit of kilogram per cubic meter (kg/m3). Moreover, the units of measuring volume are cubic millimeters (mm3), cubic centimeters (cm3), and cubic meters (m3). The units of measuring weight are kilogram (kg) and gram (g). you can perform FE simulations by using these units. The best set of units will depend on the problem.
What are The fundamental units in the SI system?
The fundamental units in the SI system are the second for time, length in meters (m), mass in kilograms (kg), time in seconds (s), the temperature in degrees Kelvin (K), and electric current in Amperes (A), amount of substance in mole, and luminous intensity in candela.
How to choose different Abaqus units to pass self-consistency?
In this section, the relation between some of the derived units and fundamental units using the symbols of Abaqus units is determined. You may use these relations to determine the desired dimension unit and implement a similar way for any other unit you may need (Unit Abaqus).
Consider the symbols for three dimensions Length (L), Mass (M), and Time (T) as mentioned in Table 1. Therefore, you can define derived units based on these fundamental dimension units as below:
Thank you for being with us in this article. In order to always provide you with up-to-date and engaging content, we need to be familiar with your educational and professional experiences so that we can offer articles and lessons that are most useful to you.
| ✅ Subscribed students | +80,000 |
| ✅ Upcoming courses | +300 |
| ✅ Tutorial hours | +300 |
| ✅ Tutorial packages | +100 |

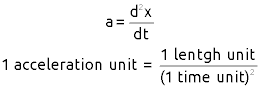
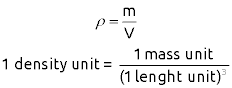
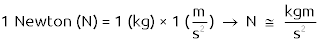

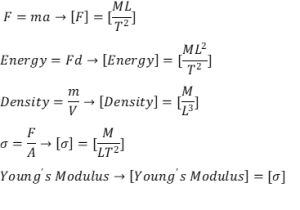
Thank you for this useful article. I simulated a model in Abaqus correctly but the output results were unacceptable. According to this article, I realized that the problem is with the measurement units. This helped me a lot