1. Introduction:
Have you ever faced an Abaqus negative eigenvalues warning message? Do you wonder why the Abaqus system matrix has negative eigenvalues? This article provides the right and accurate answer to the negative eigenvalues error in Abaqus. In most cases, it is related to the loss of stiffness or uniqueness. Examples of situations where these problems are encountered include the onset of structural buckling or material instability. In this post, ‘The CAE Assistant,’ we cover all the reasons and solutions related to this warning.
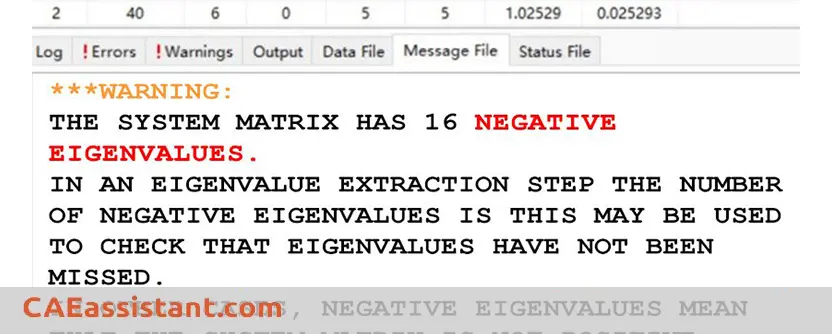
Generally, Abaqus issues such warnings when the system matrix is not positive definite. Mathematically, the appearance of a Abaqus negative eigenvalue indicates the lack of positive definiteness in the system matrix.
As you know, in general, a finite-element problem is written as:
F = K x
Where F, K, and x are the vectors of nodal load, stiffness matrix, and nodal displacement vector, respectively.
Then a positive-definite system matrix K will be non-singular and satisfy if:
For all nonzero x. Thus, when the system matrix is positive definite, any displacement the model experiences will produce positive strain energy.
Abaqus negative eigenvalues messages are generated during the solution process when the system matrix is being decomposed. Physically, negative eigenvalue messages are often associated with a loss of stiffness or solution uniqueness in the form of either material instability or the application of loading beyond a bifurcation point (possibly caused by a modeling error). During the iteration process, the stiffness matrix can then be assembled in a state which is far from equilibrium, which can cause the warnings to be issued.
After reading this article, I recommend joining our free Abaqus course. In the course, you’ll be able to work through several examples using Abaqus subroutines, Python scripting, and various other exercises. You may come across Abaqus errors and warnings, including the one discussed in this article: ‘Abaqus negative eigenvalues warning.’
2. Main Reasons for Abaqus Negative Eigenvalues Warnings
In practice, the messages can be issued for a variety of reasons, some associated with the physics of the model and others associated with numerical issues. If your analysis encounters negative eigenvalues in Abaqus, you may receive the message: ‘Abaqus system matrix has negative eigenvalues.’ Additionally, as you can see in this picture, Abaqus provides some main reasons for this warning:
There are some situations in which Abaqus negative eigenvalues messages can appear:
1. Negative eigenvalue buckling Abaqus:
Buckling analyses in which the pre-buckling response is not stiff and linear elastic.
In this case, the negative eigenvalues often point to not-real modes. Remember that the formulation of the buckling problem is predicated on the response of the structure is stiff and linear elastic prior to buckling.
2. Unstable material response:
This is another reason that can lead to an Abaqus negative eigenvalues warning. It can be due to any of three reasons:
- A hyper-elastic material becoming unstable at high values of strain.
- The onset of perfect plasticity.
- Cracking of concrete or other material failures that cause softening of the material response.
3. Anisotropic Elasticity
The use of anisotropic elasticity with shear moduli that are unrealistically very much lower than the direct moduli. In this case, ill-conditioning may occur, triggering negative eigenvalues during shearing deformation.
4. A non-positive-definite shell section stiffness is defined in a UGENS routine.
5. Pretension Node
The use of a pretension node that is not controlled by using the *BOUNDARY option and lack of kinematic constraint of the components of the structure. In this case, the structure could fall apart due to the presence of rigid body modes. The warning messages that result may include one related to negative eigenvalues.
6. Some applications of hydrostatic fluid elements.
7. Rigid body modes due to errors in modeling (not enough BC, …)
Abaqus negative eigenvalues warnings may occasionally appear alongside other warnings, which address issues like excessive element distortion or the magnitude of the current strain increment. This means that you might not encounter the specific ‘System matrix has negative eigenvalues Abaqus’ warning, even though the underlying issue is still related to Abaqus negative eigenvalues.
In cases where the analysis will not converge, the resolution of the non-convergence will often eliminate the negative eigenvalue warnings as well.
For analyses that do converge, carefully check the results if the warnings appear in converged iterations. A common cause of Abaqus negative eigenvalues warnings are the assembly of the stiffness matrix about a non-equilibrium state.
In these instances, the warnings will normally disappear with continued iteration, and, if there are no warnings in any iterations that have converged, warnings that appear in non-converged iterations may safely be neglected. If the warnings appear in converged iterations, however, the solution must be checked to make sure it is physically realistic and acceptable. It may be the case that a solution satisfying the tolerance for convergence has been found for the model while it is in a non-equilibrium state.
I hope now you can identify the cause of your warning message. We’ve made an effort to list all the common reasons leading to the Abaqus negative eigenvalues warning. We are enthusiastic about receiving your feedback. Please feel free to share any comments or questions with us. Your input will bring us one step closer to achieving our goal of becoming your ultimate CAE assistant. Our primary reference is the Abaqus Documentation, and you can also explore our packages by checking out the Abaqus tutorial.
3. How to learn the basic concepts of Abaqus?
Although this article will help you to start your Abaqus project, FEM simulation is a little complicated, and based on our feedback from hundreds of students and researchers during the last three years, the Free Abaqus course has saved a lot of time when simulating in Abaqus, and prepared codes in this package without any bugs or errors can speed up your simulation.
Get this article as a PDF file: System matrix has negative eigenvalues Abaqus
When does Abaqus give negative eigenvalues warning?
During the solution process, Abaqus checks to ensure the system is in equilibrium and stable. The basic reason for this warning message is stability. Mathematically, the appearance of a negative eigenvalue means that the system matrix is not positive definite. Therefore, if Abaqus gives this warning, it means the stiffness matrix has become unstable.
What causes to get negative eigenvalues errors?
In practice, the messages can be issued for a variety of reasons, some associated with the physics of the model and others associated with numerical issues. Physically, negative eigenvalue messages are often associated with a loss of stiffness or solution uniqueness in the form of either material instability or the application of loading beyond a bifurcation point (possibly caused by a modeling error).
What is the reason for negative eigenvalue warnings in convergent analyses?
For analyses that do converge, if the warnings appear in converged iterations, however, the solution must be checked to make sure it is physically realistic and acceptable. It may be the case that a solution satisfying the tolerance for convergence has been found for the model while it is in a non-equilibrium state.
What should be done to correct Abaqus negative eigenvalues?
There are some recommendations to remove the instability warning. The user should re-evaluate material models. Then, re-check to ensure realistic all boundary conditions and loading conditions. After that, find the areas that might be buckling or overly strained.
When does the instability of the solution occur due to the unstable behavior of the material?
The unstable material model response occurs in some situations, such as:
- A hyper-elastic material becomes unstable at high values of strain.
- The onset of perfect plasticity.
- Cracking of concrete or other material failures that cause softening of the material response.
| ✅ Subscribed students | +80,000 |
| ✅ Upcoming courses | +300 |
| ✅ Tutorial hours | +300 |
| ✅ Tutorial packages | +100 |