ABAQUS
Abaqus for Civil Engineering Part-1
The "Abaqus for Civil Engineering” package is a comprehensive and invaluable resource designed to cater to the needs of civil engineering professionals, students, and enthusiasts alike. This all-inclusive package comprises a collection of several specialized tutorial packages, making it an essential tool for mastering various aspects of civil engineering.
With this package, you gain access to an extensive library of high-quality video tutorials that cover a wide range of topics within civil engineering. Each tutorial provides clear, concise, and engaging explanations of fundamental concepts, advanced techniques, and practical applications.
DISP and VDISP Subroutines in ABAQUS
In a very simple form, DISP and VDISP subroutines are used to define user-defined boundary conditions. For example, when you need to define a boundary condition to be time-dependent, location-dependent, or even both, you should use the DISP and VDISP subroutines. ABAQUS features cannot be sufficient for problems with location-dependent and time-dependent boundary conditions simultaneously. In these cases, this subroutine can be useful to solve the challenges. In This package, you will understand the usages of these subroutines and how to work with them in three conceptual and simple workshops.
Hydroforming simulation in Abaqus
Notice: This package will be available one week after purchase.
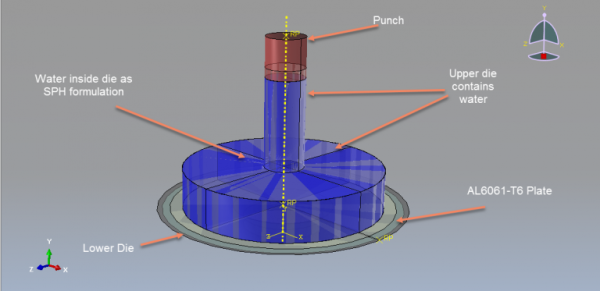
Hydroforming is a metal forming process that allows the shaping of various metals, such as steel, stainless steel, copper, aluminum, and brass. It is a cost-effective and specialized form of die molding that utilizes highly pressurized fluid to shape the metal. Hydroforming can be classified into two main categories: sheet hydroforming and tube hydroforming. Sheet hydroforming uses a single die and a sheet of metal, while tube hydroforming involves expanding metal tubes using two die halves. Hydroforming simulation in Abaqus is a valuable tool for optimizing the hydroforming process. It enables engineers to predict and analyze important factors such as material flow, stress distribution, thinning, and wrinkling during the forming process. By accurately simulating the hydroforming process, engineers can optimize key parameters like fluid pressure, die design, and material properties to achieve the desired shape with minimal defects. In this package, you will learn hydroforming process simulation with the SPH method and using time-pressure curve.
Arc welding simulation in Abaqus
Notice: This package will be available one week after purchase.
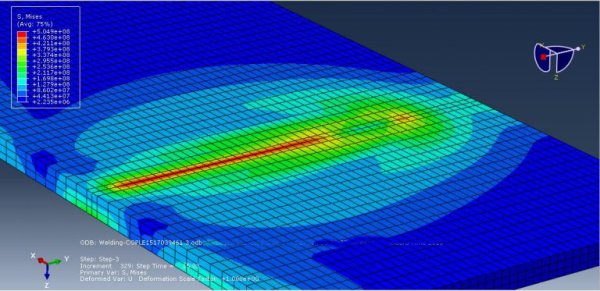
Arc welding is a fusion process that involves joining metals by applying intense heat, causing them to melt and mix. The resulting metallurgical bond provides strength and integrity to the welded joint. Arc welding is widely used in various industries for fabricating structures and components. Arc welding simulation in Abaqus is essential for optimizing the welding process and ensuring high-quality welds. It allows engineers to predict and analyze factors such as temperature distribution, residual stresses, distortion, and microstructure evolution during welding. By accurately simulating the welding process, parameters like welding speed, heat input, and electrode positioning can be optimized to achieve desired weld characteristics and minimize defects.
Tunnel excavation simulation using TBM in Abaqus
Notice: This package will be available one week after purchase.
Tunnel Boring Machines (TBMs) are advanced construction equipment used to excavate tunnels with efficiency and precision. These massive machines consist of a rotating cutting wheel equipped with disc cutters, which excavate the soil or rock, and a conveyor system that removes the excavated material from the tunnel. TBMs play a crucial role in various industries, including transportation, mining, and underground infrastructure development. TBM simulation is of utmost importance in the planning and execution of tunneling projects. It allows engineers and project managers to evaluate the feasibility of different tunneling methods, optimize the design and operation of TBMs, and predict potential challenges and risks. By simulating the TBM's performance and behavior under various geological conditions, factors such as ground stability, excavation rates, cutter wear, and potential impacts on surrounding structures can be analyzed and mitigated. In this package, you will learn how to do a TBM simulations by several practical examples.
Blood Flow Analysis in Abaqus
Notice: This package will be available one week after purchase.
Human blood is a vital fluid that circulates through the body, carrying oxygen, nutrients, hormones, and immune cells. Simulation of human blood is crucial for understanding cardiovascular diseases, hemodynamics, and therapeutic interventions. It enables researchers to study the complex behavior of blood flow, investigate disease mechanisms, and develop improved diagnostic and treatment strategies. This package contains three workshops that would help you simulate blood flow in vessels: “Human blood with coronary vessel Fluid Structure Interaction simulation in Abaqus”, “Blood and vessel FSI simulation using Abaqus-Co Simulation process”, and “Non-Newtonian blood flow Simulation in Abaqus”.
Friction Stir Welding (FSW) Simulation in Abaqus
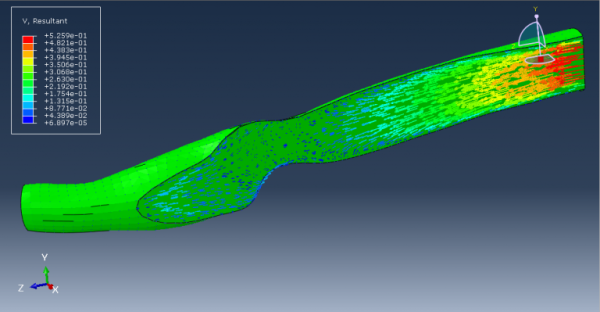
Friction stir welding (FSW) is a solid-state joining process that utilizes a rotating tool to generate frictional heat, enabling the consolidation of materials without melting. FSW offers numerous benefits and is particularly valuable for welding challenging materials like aluminum alloys. It finds widespread applications in industries such as automotive, aerospace, shipbuilding, and construction, providing enhanced strength, weight reduction, and structural integrity. FSW minimizes distortion, reduces the need for post-weld machining, and eliminates issues related to solidification and cooling. Simulations using Abaqus, a popular finite element analysis software, play a crucial role in optimizing FSW processes. Engineers can investigate process parameters, evaluate weld quality, predict residual stresses and distortions, and optimize weld designs through Abaqus simulations. These simulations enable cost-effective development, improved weld quality, reduced material waste, and enhanced productivity in industrial applications. In this package, you will learn how to simulate FSW simulations in a variety of examples with different methods.
Simulation of Hyperelastic Behavior of Materials
Learn to simulate the mechanical behavior of soft materials like polymers and hydrogels using Abaqus. Understand hyperelasticity and the strain-energy equations that describe it. Discover different models for this behavior, choose the best one, optimize its parameters, and ensure it works well for your material. Validate your simulation with real-world data. Finally, master Abaqus tools to set up and run simulations for hyperelastic materials and structures.
Pre-Order Now
Coming soon...
Soil Impact Analysis in Abaqus
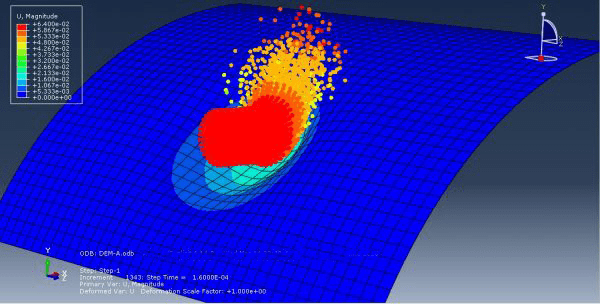
Soil impact refers to the interaction between a solid object and the soil, wherein the object collides with or penetrates into the soil. This issue holds great importance across various industries, including civil engineering, geotechnical engineering, construction, and transportation. Understanding soil impact behavior is crucial for designing and assessing the safety and performance of structures and systems subjected to dynamic loads, such as vehicle collisions, pile driving, and projectile impacts. Simulation plays a vital role in studying soil impact. By employing advanced numerical methods and software tools like Abaqus, researchers and engineers can accurately model and analyze the complex interactions between objects and soil. Simulation allows for the investigation of various parameters, such as impact velocity, soil properties, object geometry, and boundary conditions, to assess their influence on the response and behavior of the system. In this package, you will learn how to do soil impact simulations in several practical examples.
Low-Velocity Impact simulation in Abaqus
Low-velocity impact refers to the collision between objects at relatively low speeds. While the impact energy may be lower compared to high-speed impacts, low-velocity impacts can still cause significant damage and deformation. Assessing the effects of low-velocity impact is crucial for various industries to ensure the structural integrity, safety, and performance of their products. For example, in the automotive industry, understanding the response of vehicles to low-velocity impacts is essential for designing crashworthy structures and improving occupant safety. In aerospace, assessing the impact resistance of aircraft components, such as fuselage panels or wings, helps ensure their ability to withstand ground handling incidents or bird strikes. In this package, you will learn how to do low-velocity impact simulations with several practical examples.
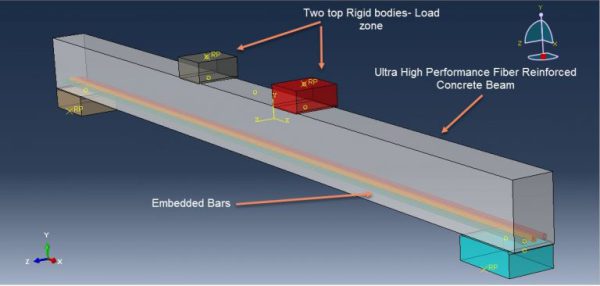
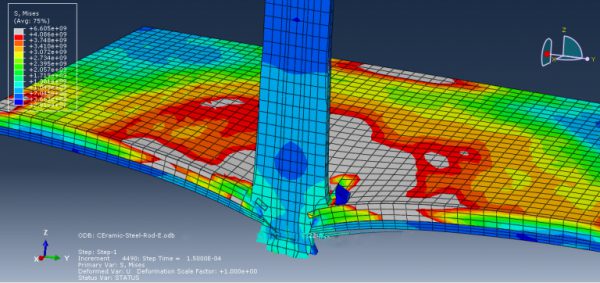
Ultra-High-Performance Fiber Reinforced Concrete (UHPFRC) structures in Abaqus
Notice: This package will be available one week after purchase.
UHPFRC (Ultra-High-Performance Fiber Reinforced Concrete) structures have emerged as a groundbreaking innovation in construction. These structures offer exceptional strength, durability, and performance, revolutionizing the industry. UHPFRC incorporates a precise combination of Portland cement, fine aggregates, admixtures, and steel or synthetic fibers, resulting in an extraordinarily dense and robust composite material. With compressive strengths exceeding 150 MPa, UHPFRC structures exhibit enhanced resistance to cracking, increased load-bearing capacity, and improved durability against environmental factors such as corrosion and freeze-thaw cycles. The superior mechanical properties of UHPFRC enable the design of slimmer and lighter elements, leading to reduced material consumption and more sustainable construction practices. UHPFRC structures find applications in various fields, including bridges, high-rise buildings, marine structures, and precast elements, offering long-term performance and contributing to the advancement of modern construction. In this package, you will learn how to simulate these structures with many practical examples.
Modeling Functionally Graded Materials (FGMs) in ABAQUS
Dive into the realm of innovative engineering with our comprehensive tutorial package, designed to empower you in modeling Functionally Graded Materials (FGM) using the Abaqus USDFLD subroutine. Uncover the fascinating world of FGMs, materials that ingeniously vary their composition and microstructure, offering a nuanced control over mechanical, thermal, and other properties.
The workshop component takes you on an exploration of crack paths in Spherical Functionally Graded Materials, emphasizing simulation techniques using Abaqus Standard and the USDFLD subroutine. Uncover the secrets of stress distribution within a pressured, empty sphere, and enhance your skills by implementing the XFEM method for precise crack characterization. This training ensures you gain valuable insights into subroutine development, empowering materials engineers and designers to innovate and elevate the performance of structures across various industries. Embark on your journey to mastery with this all-encompassing tutorial package.
High-Velocity Impact Simulation in Abaqus
High-velocity impact refers to the collision between two bodies at extremely high speeds, typically involving projectiles and targets. It is a phenomenon of great interest in various fields, including defense, aerospace, and automotive industries. High-velocity impact simulation in Abaqus is a computational approach used to analyze and predict the behavior of materials and structures subjected to such impacts. Abaqus, a powerful finite element analysis software, enables engineers and researchers to model and simulate the complex interactions between impacting bodies, accurately predicting factors like stress, strain, deformation, and damage. By simulating high-velocity impacts in Abaqus, engineers can gain valuable insights into the performance and integrity of materials and structures, ultimately aiding in the design of safer and more resilient systems. In this package, you will learn how to do these simulations in many practical examples.
Composite Pressure Vessel simulation in ABAQUS
Pressure vessels are made using different methods today, and one of them is filament winding. This package shows the simulation of composite pressure vessels made using the filament winding method.
In this training package, three winding methods, planar, geodesic, and isotensoid, have been taught for filament winding pressure vessels. In this tutorial, two general methods also have been presented for simulating filament wound pressure vessels. One uses the Abaqus graphical user interface(GUI), and the other uses the Python script. On the other hand, two criteria, Tsai-Hill and Puck, have been used to model damage in the composite. A UMAT subroutine has been used to use the Puck criterion.
Hypermesh Course for Beginners
This training package includes workshops that help you to learn about basics of hypermesh and how to use it. This is the most comprehensive tutorial containing ways to do the basic designing, importing and exporting abaqus file.
The subjects such as creating lines,nodes,2D mesh, surfaces, creating tetramesh, creating 3d bodies,enhancing mesh quality etc are covered in this tutorial.
Pre-Order Now
Coming soon...
Composite pressure vessel analysis with Semi-Geodesic winding
Nowadays, pressure vessels are produced using various methods, one of which is filament winding. This package teaches the simulation of composite pressure vessels produced using the filament winding method. Filament winding itself has different methods, and one of the most widely used winding methods for producing composite vessels is the semi-geodesic filament winding method. In this package, first, the semi-geodesic method is described. Then, the simulation of a semi-geodesic vessel is performed using a Python script. Additionally, a UMAT subroutine is used to simulate the failure of composite materials used in the vessel.
Full Composite fatigue Add-on (Academic and industrial usage)
This package is designed to instruct users on how to utilize the composite fatigue modeling Add-on, which removes the need to write a subroutine for composite fatigue modeling. Instead, users can select the composite type, input material properties, and generate the subroutine by clicking a button. The Add-on includes four types of composites, and the generated subroutine for all types is the UMAT. These four types are Unidirectional, Woven, short fiber composites (chopped), and wood. The fatigue criteria used for each type are the same as its respective package. For example, the fatigue criteria for woven composites are identical to that used in the "Simulation of woven composite fatigue in Abaqus" package. This Add-on provides a simple graphical user interface for composite fatigue modeling, which can be utilized for both academic and industrial applications.
Pre-Order Now
Coming soon...
Full Composite damage Add-on (Academic and industrial usage)
This package will teach you how to use the composite damage modeling Add-on. The Add-on eliminates the need for writing a subroutine for composite damage modeling. Instead, you only need to select the desired composite type, input the material properties, and click a button. The Add-on will then generate the subroutine for you. The Add-on includes four types of composites: Unidirectional, Woven, short fiber composites (chopped), and wood. The generated subroutine for all types is the VUSDFLD. The damage criteria used in each type is the same as the one used in its respective package. For instance, the damage criteria for the woven composite is identical to the one used in the "Simulation of woven composite damage in the Abaqus" package. This Add-on offers a user-friendly graphical user interface for composite damage modeling, which can be used for academic and industrial purposes.
Pre-Order Now
Coming soon...
Optimization in ABAQUS
Notice: 2 hours of the package is available now; during 1-month after purchase, it will be completed.
Optimization is a process of finding the best solution to a problem within a set of constraints. It involves maximizing or minimizing an objective function while satisfying a set of constraints. Optimization in Abaqus involves the use of advanced algorithms and techniques to improve the design of structures and systems. Abaqus provides a range of optimization tools, including topology optimization, size optimization, and shape optimization. These tools help in improving the performance of structures by reducing their weight, increasing their stiffness, and minimizing their stress levels. In this package, all types of optimization, such as Topology, will be discussed; after each lesson, there will be workshops to help you to understand optimization with practical examples.
Script to transfer load from CFD to structural model in Abaqus
Notice: This package will be available 1 month after purchase in your dashboard.
FEA offers various loading types, such as force, pressure, and temperature, which can be applied to different parts of an object, such as points, surfaces, edges, nodes, and elements. Therefore, applying accurate loading conditions on these features is necessary for reliable simulation results and the safe design of structures. Sometimes, the loading conditions are obtained by another analysis, such as CFD, and need to be transferred and applied to the structural model for the structural analysis; during this transfer, the loads might not be appropriately applied to the model, especially when the loads are complicated like the pressure profile of a space rocket. So in this package, a Python script is presented to solve this issue and transfer the loads properly to the structural model.
Buckling and Postbuckling | stability of shell structures in Abaqus
The present ABAQUS tutorial is an introduction to the stability of shell structures according to the European Design Standard EN 1993-1-6. The package presents all the important steps to model and analyze especially cylindrical shells under different load cases (axial compression, bending, torsion, shear, gravity load). The package consists of two main parts: a beginner section that shows how to model regular shells and stiffened shells and an advanced section that shows the modeling and analysis of an wind turbine tower according to EN 1993-1-6.
Bolt Modeling in Abaqus
Bolts and joints play a vital role in the stability and structural integrity of various engineering structures, including buildings, bridges, and machines. Bolts are used to fasten or connect different components together, providing a means of transferring loads and ensuring the continuity of load paths. Joints connect structural elements, allowing them to move and deform while maintaining their overall stability. Proper design and selection of bolts and joints are crucial to ensuring the safety and durability of the structure. Factors such as the type of load, the materials used, and the environmental conditions must be considered when selecting bolts and joints. Failure to properly design and install bolts and joints can result in catastrophic failure of the structure. In this package, you will learn how to model bolts and joints, simulating the failure of connections and other things with practical examples.
Car part industrial simulation
Car industrial parts are complex and critical components that play a vital role in the operation of a car. Two such parts are the exhaust manifold and the internal combustion engine (IC engine). The exhaust manifold directs hot exhaust gases from the engine's cylinders into the exhaust system and is typically made of cast iron or stainless steel. The IC engine converts fuel into mechanical energy by burning fuel in a controlled explosion within the engine cylinder. High temperatures and pressures must be considered in the design, and the components must be made of durable materials that can withstand the stresses of constant combustion. Therefore, it is important to know how these parts respond under different loading conditions to have the best design possible. In this package, there are two workshops to help you with this job: Heat transfer analysis in an exhaust manifold and Thermomechanical analysis of an exhaust manifold.
Rock simulation in Abaqus
Rock simulation is essential for evaluating the behaviour of rock masses under various loading conditions, such as earthquakes, landslides, and blasting. It enables engineers and geologists to assess the stability and integrity of rock structures, predicts potential failure modes, and develop effective mitigation strategies. Rock simulation is crucial in the design and planning of mining operations, tunnels, and underground constructions to ensure the safety and longevity of the structures. It also plays a vital role in assessing the seismic hazard of an area and evaluating the potential impact of earthquakes on the built environment. In this package, you will learn how to do an impact simulation on a granite stone using the JH-2 model; also an explosion simulation inside a rock for excavation purposes. You can learn more detail in the description of the workshops.