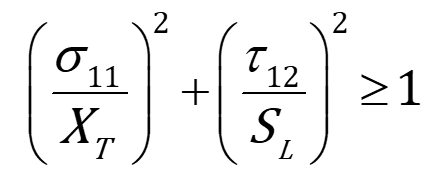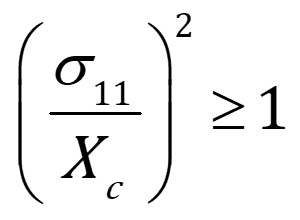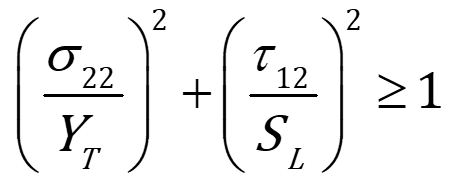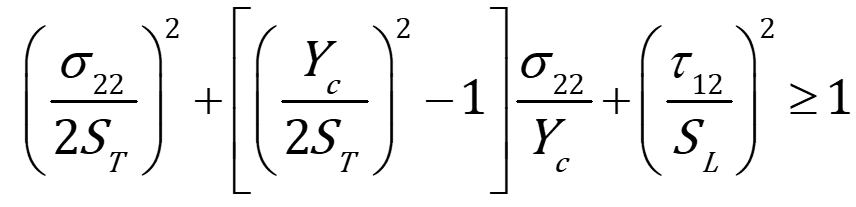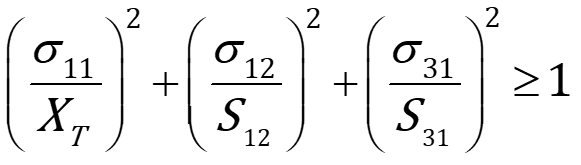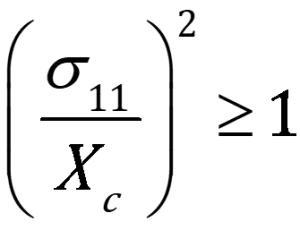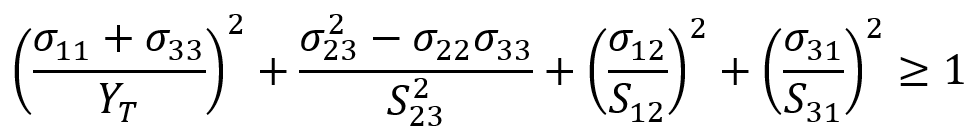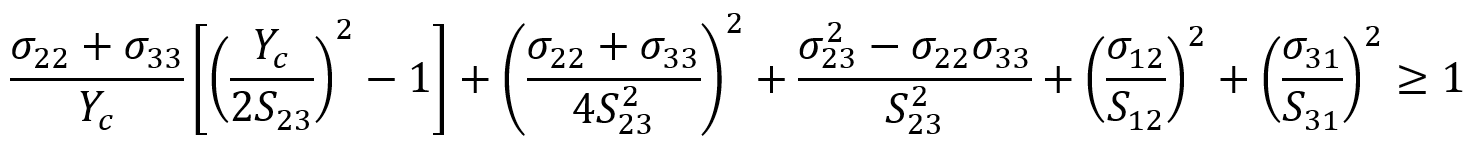What is Hashin Failure Criteria? | Hashin Damage in Abaqus

How do we predict the exact moment a composite material will fail under pressure? The Hashin Failure Criteria offer a powerful answer by breaking down the complex failure behaviors of fiber-reinforced composites, helping engineers foresee how and when damage will occur.
The Hashin Damage Criteria are specifically developed for fiber-reinforced composites. It identifies whether failure occurs in the fibers or the matrix, giving a clearer picture of the material’s behavior under stress. This approach makes it suitable for simulations, especially when multiple types of stresses are involved, which is common in real-world applications.
In this blog, we’ll dive into the Hashin Damage Criterion, explaining both the 2D and 3D forms and how they differ. We’ll also explore Hashin Damage Criteria in Abaqus using both the Graphical User Interface (GUI) and subroutines like UMAT, providing insights into how engineers can use this powerful theory for simulating composite material damage.
What included in this FREE downloadable file?
1. What are the Hashin Failure Criteria?
The Hashin Failure Criteria is a failure theory designed to predict different types of damage in composite materials such as fiber-reinforced composites. Developed by Zvi Hashin, this criterion distinguishes between fiber and matrix failure, providing a more detailed failure mechanism prediction for composites compared to traditional criteria like the maximum stress or strain theories.
The Hashin failure criteria separate failure modes based on whether the damage is occurring in the fibers or the matrix. It uses different equations for different types of damage, based on the physical failure modes typically seen in composites. This makes the criterion more accurate when applied to complex materials like fiber-reinforced polymers.
The Hashin criterion is an interactive failure criterion because it involves multiple stresses interacting, not just the independent tensile or shear stress. This makes it very appropriate for composite materials, where multiple stresses contribute to failure simultaneously.
1.1. Damage in Composite Materials
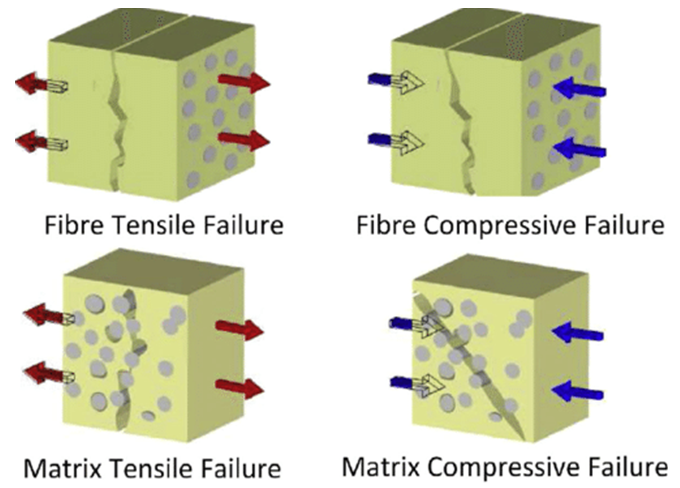
Composite materials, such as fiber-reinforced polymers, experience damage through various mechanisms due to their heterogeneous nature. Damage in composites is complex and can occur in different forms:
- Matrix Cracking: Cracks can form in the matrix (the polymer or resin) of the composite, leading to a loss of load-bearing capacity.
- Fiber Breakage: Fibers, which are the main load carriers, can break under stress, leading to a significant loss in stiffness and strength.
- Delamination: The separation of layers in laminated composites is known as delamination, which can greatly weaken the structure.
- Fiber-Matrix Debonding: The bond between fibers and the matrix may fail, causing a reduction in the ability to transfer load between the matrix and the fibers.
Figure 1: Damaged composite material [Ref]
1.2. Why Hashin’s theory?
The Hashin failure criteria are used due to its ability to predict failure in both the matrix and fibers. This criterion is used in computational simulations like finite element analysis (FEA) when accurate prediction of composite material failure is required. We used this theory because:
- Accuracy in Composite Failure Prediction: Unlike maximum stress or strain theories, Hashin’s criterion considers the different modes of failure in both the fibers and the matrix, offering a more accurate representation of how composites fail.
- Separate Failure Modes for Fiber and Matrix: Hashin’s criterion separately evaluates the failure of the fibers and the matrix, allowing for distinct and realistic failure predictions for both parts of the composite.
- Versatility: It can be used for both tension and compression failure modes, making it suitable for a wide range of loading conditions.
- Implementation in FEA: The Hashin criterion is commonly implemented in finite element software (such as Abaqus), enabling detailed simulations of composite material behavior.
- Applicable to Complex Loading: It accounts for combined loading conditions, which is common in real-world applications of composites.
| If you need deep training, our Abaqus Course offerings have you covered. Visit our Abaqus course today to find the perfect course for your needs and take your Abaqus knowledge to the next level! |
2. 2D and 3D form of Hashin Damage Criteria Theory
The Hashin Damage criteria (hashin failure criteria) can be applied in both 2D and 3D stress states. The fundamental idea is the same in both forms, but the stress components considered vary depending on whether the analysis is in two or three dimensions.
The primary difference between the 2D and 3D forms of the Hashin damage criteria lies in the number of stress components involved:
- 2D Form: In 2D, we typically deal with a plane stress state, which includes normal stresses in two directions (
) and shear stress in the plane (
).
- 3D Form: In 3D, the stresses are expanded to include normal stresses in three directions (
) and shear stresses in all three planes (
).
In general, the 2D analysis focuses on two directions within the plane (often referred to as the 1-2 plane), while 3D analysis includes all the stresses such as the out-of-plane stresses.
Figure 2: 2D and 3D stress components
2.1. 2D Hashin Damage Criteria (hashin failure criteria) Theory
In the 2D Hashin failure criteria, we focus on the in-plane stresses. The equations for failure in tension and compression of the fibers and matrix are derived based on these in-plane stress components.
- Fiber Tension (2D):
For fiber tension, the criterion is:
Where:
is the longitudinal stress in the fiber direction.
is the longitudinal tensile strength of the fibers.
is the shear stress.
is the longitudinal shear strength.
If this condition is satisfied, fiber failure in tension occurs.
Want to learn more damage criteria for composite materials? In the Introduction part of the package below we have introduced all.
- Fiber Compression (2D):
For fiber compression:
Where is the longitudinal compressive strength of the fibers. This equation is simpler because the compressive failure of fibers is governed mainly by longitudinal stress.
- Matrix Tension (2D):
For matrix tension, failure is governed by:
Where:
is the transverse normal stress (stress in the direction perpendicular to the fibers).
is the transverse tensile strength of the matrix.
- Matrix Compression (2D):
For matrix compression, failure occurs if:
Where:
is the transverse compressive strength of the matrix.
is the transverse shear strength.
In 2D, we only consider the stresses in the 1-2 plane (in-plane longitudinal, transverse, and shear stresses), which simplifies the analysis and equations. If any of the four conditions mentioned above are met, it means the failure of the composite from the point of view of the Hashin failure criteria.
2.2. 3D Hashin Failure Criteria Theory
In the 3D Hashin failure criteria, the equations expand to include the stresses in the third direction (the 3rd axis, out-of-plane direction). This results in a more comprehensive analysis of failure because out-of-plane stresses are crucial in many real-world applications.
- Fiber Tension (3D):
The failure criterion for fiber tension in 3D is similar but extended:
Where:
and
are the shear stresses in different directions.
and
are the shear strength in longitudinal and transverse directions. Other terms are the same as in the 2D Hashin criterion.
- Fiber Compression (3D):
For fiber compression in 3D:
This remains the same as the 2D case because compressive failure is still largely governed by the longitudinal stress.
- Matrix Tension (3D):
For matrix tension in 3D:
- Matrix Compression (3D):
For matrix compression in 3D:
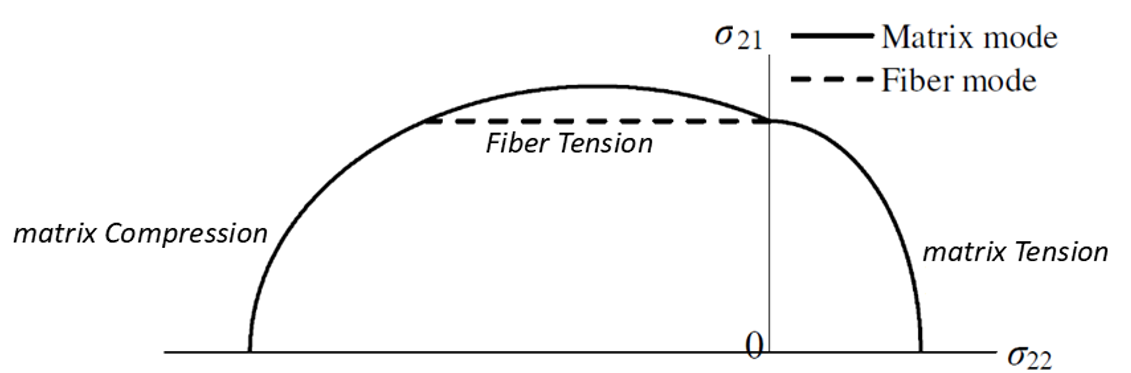
Also, in Figure 3, you can see the Hashin failure envelope, which is drawn based on the 3D Hashin relationship.
Figure 3: Failure envelope of predicted by Hashin’s criteria
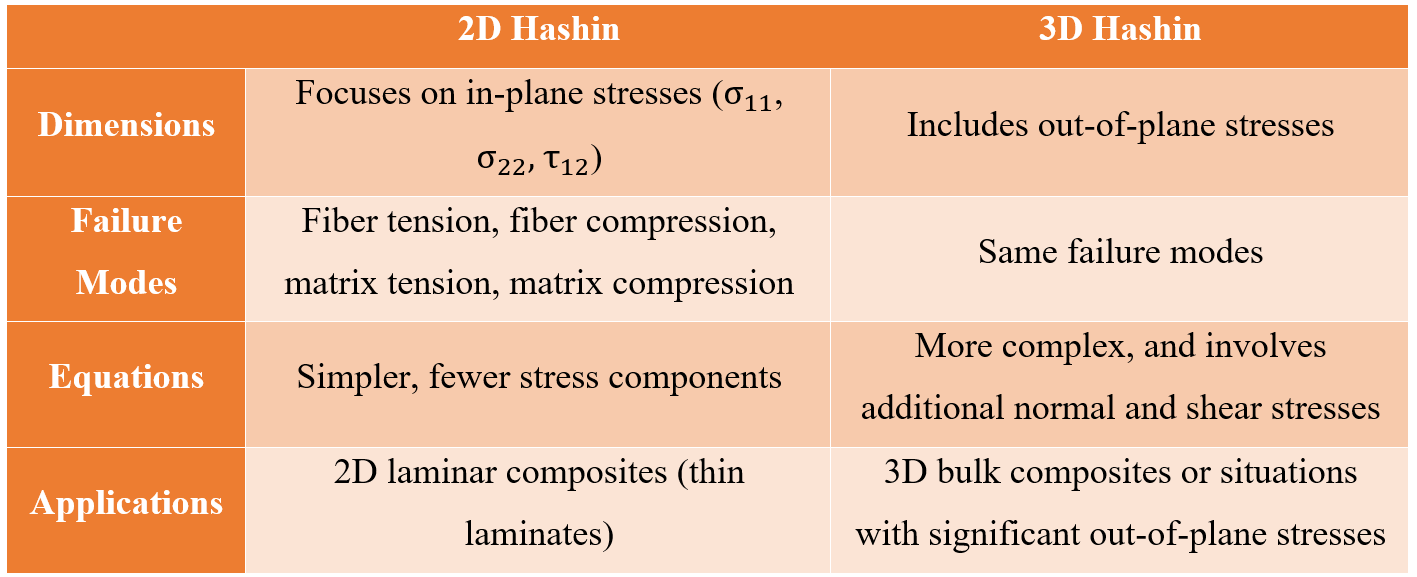
2.3. Differences Between 2D and 3D Hashin Forms
The 2D Hashin criterion is used for analyzing materials where stresses are primarily confined to two dimensions, such as in thin laminates or plate-like structures. The 3D Hashin criterion, on the other hand, is essential for thicker composite materials or where out-of-plane stresses are significant. Both forms are effective in predicting failure but are applied based on the nature of the stress state in the composite material.
Figure 4: Damage in fiber-reinforced composites [Ref]
Here, we have a complete tutorial for 3D Hashin damage simulation in Abaqus titled “3D Continuum Abaqus Hashin progressive Damage for Composite Materials“.
3. Hashin Damage Criteria in Abaqus: Using GUI and subroutines for simulation (UMAT -USDFLD)
Hashin Damage Criteria in Abaqus can be implemented directly via the Graphical User Interface (GUI) for composite damage modeling. Abaqus provides a built-in damage model that uses the Hashin criterion for fiber-reinforced composite materials, particularly for progressive damage analysis under multiaxial loading conditions. On the other hand, the Hashin criterion can be implemented using different subroutines such as UMAT in Abaqus. In the next step, we will fully explain these methods.
3.1. Damage Initiation and Damage Evolution
In Abaqus, damage initiation and damage evolution are crucial aspects of simulating failure in composite materials, especially fiber-reinforced composites. They allow users to model the onset of failure and the subsequent material degradation, providing a realistic representation of how composite structures fail under loading.
Damage initiation refers to the point at which a material begins to fail or degrade due to the applied stress or strain. For composites, damage initiation often occurs due to fiber breakage, matrix cracking, or delamination, depending on the loading conditions and material properties. In Abaqus, damage initiation is determined based on a failure criterion. For composite materials, the Hashin criterion (Hashin damage Abaqus) is commonly used, which identifies failure in fibers and matrix separately (tensile and compressive modes). You can learn how to model the damage initiation with Hashin failure criterion in the first workshop of our tutorial.
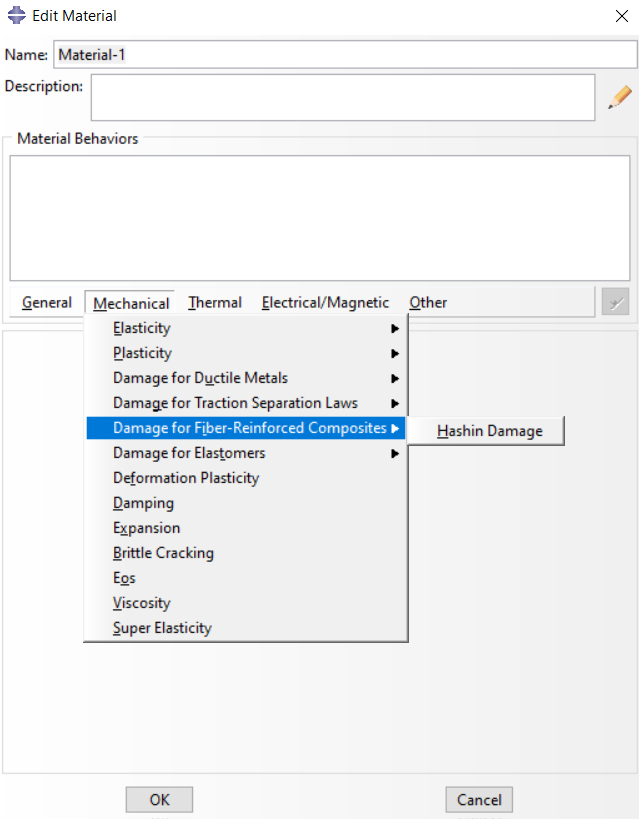
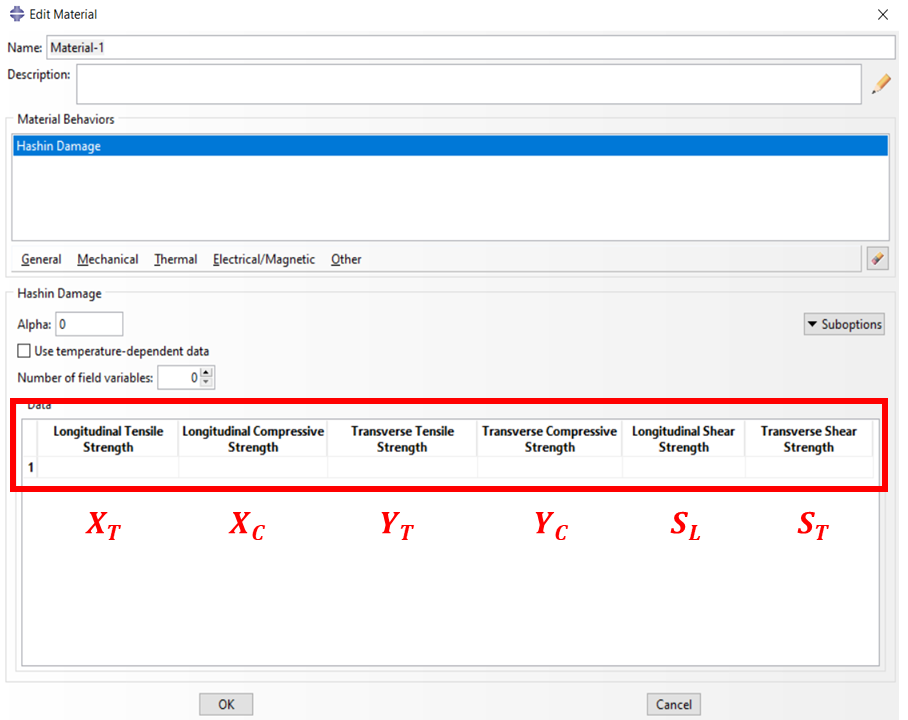
In Abaqus, damage initiation for composites is typically defined in the property module. In this module, by selecting the Damage for Fiber-Reinforced Composites option, you can access the Hashin failure criteria.
Figure 5: Hashin Damage in Abaqus
To use this criterion, the following parameters must be determined:
- Fiber tensile strength
- Fiber compressive strength
- Matrix tensile strength
- Matrix compressive strength
- Longitudinal and transverse shear strength respectively
and
.
In the figure below, the required parameters of the Hashin damage Abaqus are displayed in the software.
Figure 6: Hashin failure criterion parameters
On the other hand, damage evolution describes the progression of material degradation after damage initiation, providing a mechanism for simulating the reduction in material stiffness and strength as failure propagates. In composite materials, damage evolution is critical for modeling phenomena like fiber breakage, matrix cracking, and delamination.
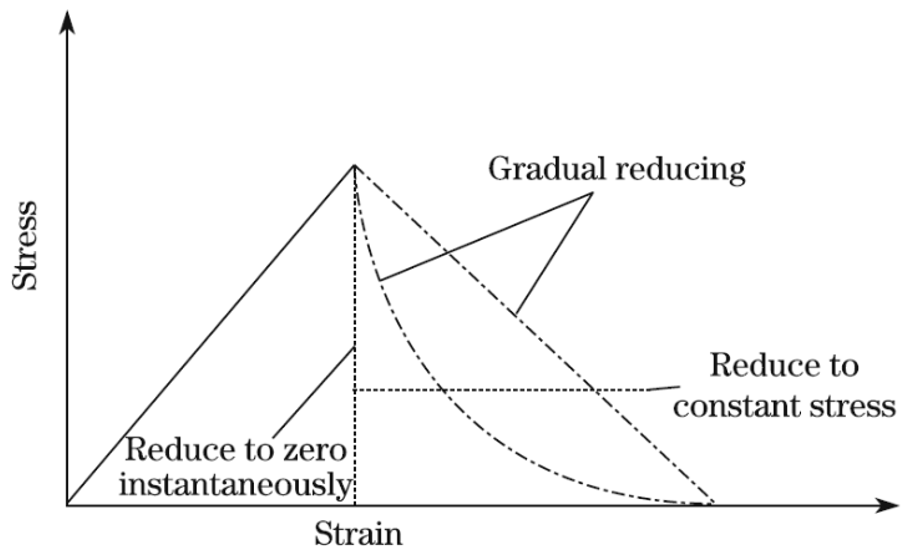
When a failure is identified at a specific material point in composite laminates, the material properties at that point must be modified based on a selected degradation model. This adjustment can occur through one of three degradation modes: an instantaneous reduction to zero, a reduction to a specified constant stress level, or a gradual reduction along a predefined path. Each approach represents a different method for modeling the loss of material integrity after damage, as illustrated in Figure.
Figure 7: Various properties reduction in composites after damage initiation
The instantaneous reduction removes all material strength at the failure point, effectively eliminating its load-bearing capacity. In contrast, the constant-stress reduction limits the stress to a fixed value even after failure, preserving some residual strength. Lastly, the gradual reduction allows for a progressive loss of strength, simulating how damage propagates over time or under continued loading. As you can see in the figure, the gradual decrease can be linear or function of different functions such as exponential.
In gradually damage once damage is initiated, the material does not fail instantly; Instead, the material properties degrade over time as the damage spreads through the structure. Damage evolution is often defined using fracture energy or energy dissipation. The idea is to simulate how much energy is absorbed by the material as cracks propagate.
Damage evolution usually includes a softening model that reduces the material stiffness after the damage initiation criterion is met. For example, the fracture energy associated with fiber or matrix failure determines how quickly the material stiffness degrades once damage is initiated.
Damage Initiation + Progressive Damage (gradual degradation based on an energy method) + Step by Step guide using VUMAT subroutine
Damage Initiation + Progressive Damage (immediate or sudden reduction in material properties upon detection) + Step by Step guide using UMAT, VUMAT, USDFLD subroutines
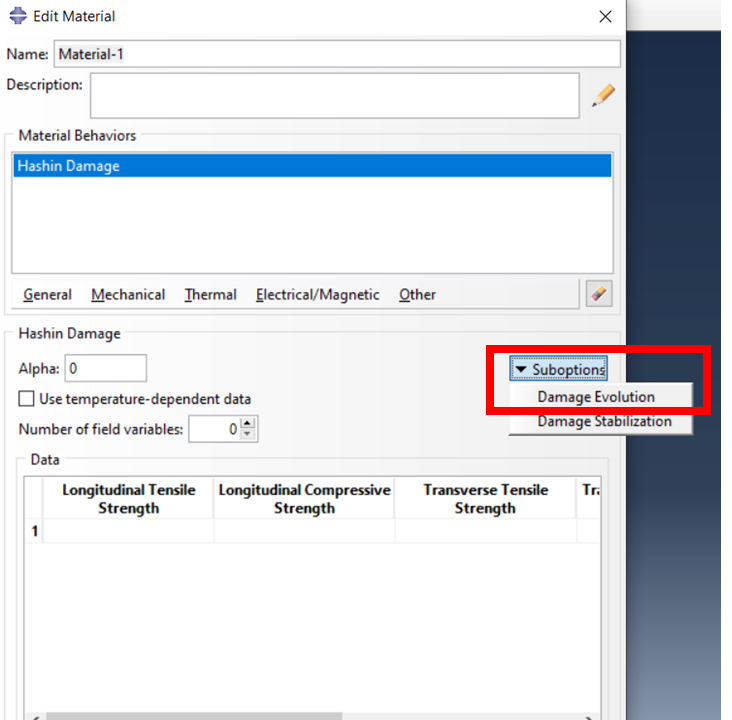
Damage evolution can be enabled after defining the damage initiation criterion. Abaqus users in the property module, after selecting Damage for Fiber-Reinforced Composites and defining the damage initiation criterion, can select Damage Evolution to specify how the damage progresses.
Remember that Abaqus only provides users with a linear progressive reduction of properties. In order to reduce the gradual properties, except the linear function, the considered function should be modeled by a subroutine. To do this, the stiffness matrix of the material, which defines the relation between stress and strain, must be determined. In the next step, we will introduce the subroutines that provide users with the ability to do this.
Figure 8: Damage Evolution option in Abaqus
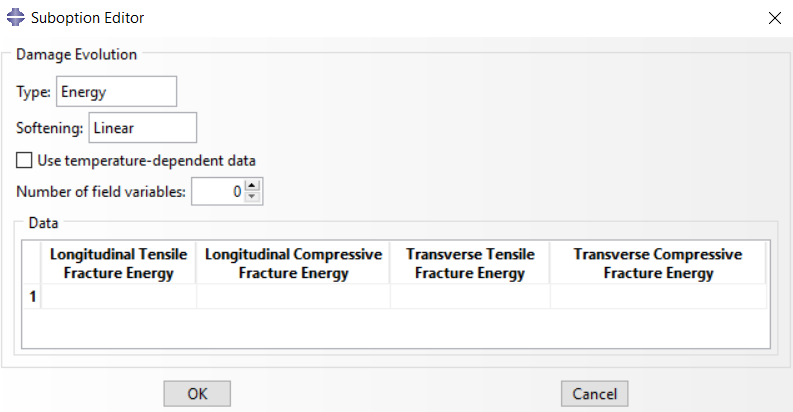
To use progressive damage, the fracture energies must be determined. These values are extracted from experimental tests and are material constants.
Figure 9: Damage Evolution parameters in Abaqus
3.2. Subroutine and Hashin failure criteria
Subroutines in Abaqus allow for user-defined material models, constitutive behaviors, and custom field variables. Abaqus has various subroutines that can be used to extend the default capabilities of the software, including:
- UMAT (User Material Subroutine): Used in Abaqus/Standard for defining custom material models for static and quasi-static problems.
- USDFLD (User-Defined Field Subroutine): Allows users to define custom field variables that affect the material response.
Note: There is a complete tutorial for UMAT and USDFLD subroutines to simulate Hashin theory in this tutorial video “Simulation of composite Hashin damage in 3d continuum element in Abaqus (UMAT-VUMAT-USDFLD)“.
Subroutines give the user the flexibility to implement more complex material models, interactions, and damage criteria that might not be available in Abaqus’ default library. But when should we use Subroutines for Hashin Damage Abaqus Modeling? You should consider using subroutines for Hashin damage Abaqus modeling when:
- Custom failure criteria are needed: If the built-in Hashin damage criteria in Abaqus are insufficient for your analysis, such as when you need to account for non-standard loading conditions or multiscale modeling.
- Progressive damage or custom damage evolution: For more complex progressive damage modeling beyond what Abaqus offers by default, subroutines allow the user to define a custom damage evolution law.
To use the UMAT subroutine for implementing Hashin failure criteria in Subroutines (Abaqus/Standard):
- Step 1: Define the Material Behavior: In the UMAT subroutine, you define the stress-strain relationship for the composite material. Use the Hashin failure criteria to calculate failure initiation and then reduce the material stiffness based on the damage state.
- Step 2: Progressive Damage: Implement a damage evolution model to reduce material stiffness as damage accumulates, updating the stress and strain at each iteration.
- Step 3: Output Variables: Define output variables (such as damage parameters) to be visualized after the simulation.
USDFLD Subroutine:
- Step 1: Custom Field Variables: Use USDFLD to define custom field variables that affect the material response, such as damage growth or strain softening.
- Step 2: Interaction with Material Model: The field variables defined in USDFLD can interact with the material model to alter the stiffness, strength, or failure behavior of the composite material based on the Hashin criterion.
Want to master composite damage in Abaqus? The Hashin Progressive Damage with VUMAT is perfect for modeling gradual damage in analyses with in-depth workshops, while the Composite Hashin Damage with UMAT, VUMAT, and USDFLD focuses on sudden damage in analyses with easy-to-implement subroutines. Click below on each of the package according to your need.
|
3D Continuum Elements + Hashin Failure Criterion + Damage Initiation + Progressive Damage (gradual degradation based on an energy method) + Step by Step guide using VUMAT subroutine |
3D Continuum Elements + Hashin Failure Criterion + Damage Initiation + Progressive Damage (immediate or sudden reduction in material properties upon detection) + Step by Step guide using UMAT, VUMAT, USDFLD subroutines |
4. Conclusion
In this article, we explored the Hashin Damage Criteria, a failure theory used to predict damage in composite materials, particularly fiber-reinforced composites. The criterion offers a detailed breakdown of failure modes, making it an essential tool for accurate simulations in finite element analysis.
Understanding the Hashin failure criteria is crucial because composite materials are widely used in various industries, and accurately predicting their failure ensures better design and safety. We first looked at different damage mechanisms in composites, like matrix cracking and fiber breakage, which the Hashin failure criteria address. Then, we explained the 2D and 3D forms of the Hashin damage criteria, showing how stress components are handled in both cases. Lastly, we discussed how hashin damage criteria in Abaqus can be implemented using the GUI or subroutines, focusing on damage initiation and evolution.
Overall, we learned that the Hashin Damage Criteria are an effective method for simulating composite material behavior, offering more precise predictions than traditional failure theories.
Explore our comprehensive Abaqus tutorial page, featuring free PDF guides and detailed videos for all skill levels. Discover both free and premium packages, along with essential information to master Abaqus efficiently. Start your journey with our Abaqus tutorial now!
The CAE Assistant is committed to addressing all your CAE needs, and your feedback greatly assists us in achieving this goal. If you have any questions or encounter complications, please feel free to share it with us through our social media accounts including WhatsApp.