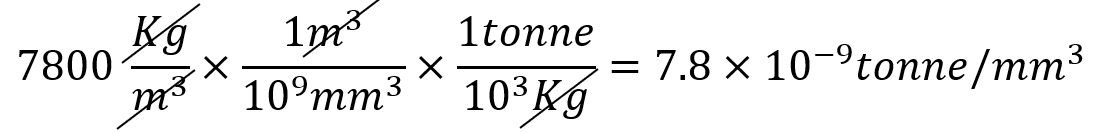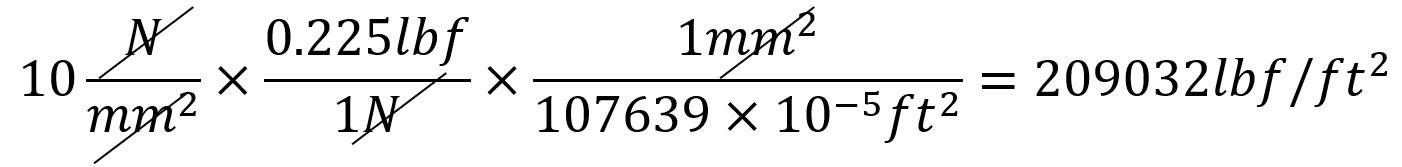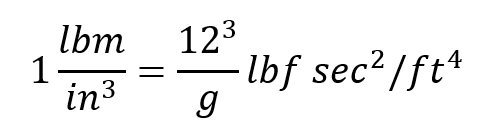Understanding units in Abaqus (Abaqus units) can be perplexing for beginners, as the software does not inherently include units for quantities such as stress, Young’s Modulus, and density. This is not unique to Abaqus; most finite element programs, like Ansys and LS-Dyna, also rely on users to ensure that numerical values are entered with consistent units.
In Abaqus, except for rotation and angle measures, the software lacks built-in units. Users must ensure that their chosen units are self-consistent, meaning derived units should be expressible in terms of fundamental units without conversion factors.
This blog will demystify how units work in Abaqus and guide you on selecting a consistent unit system. We’ll cover different unit systems like CGS, FPS, MKS, and SI units, discuss considerations and pitfalls such as round-off errors and imperial units, and provide a helpful reference table for consistent units.
1. Does Abaqus have unit system? | Abaqus Units
First, let’s make something clear; the Abaqus Does Not have a self-consistent unit system like other softwares.
When working with Abaqus, one of the first things to grasp is its approach to units (Abaqus units). Unlike some software that comes with predefined unit systems, Abaqus operates differently. Except for rotation and angle measures, Abaqus does not have any built-in units. This means that users must adopt a self-consistent unit system throughout their modeling process.
In practical terms, this means that all fundamental units (length, mass, time, etc.) and their derived units (force, pressure, etc.) need to be compatible within the chosen system. For example, if you select meters for length, kilograms for mass, and seconds for time, you must use these units consistently for all calculations and inputs. Any mismatch or conversion oversight can lead to significant errors in the simulation results.
Understanding this approach is crucial for accurate modeling and simulation in Abaqus. By ensuring that the units are consistent, users can avoid common pitfalls and achieve reliable results in their analyses (Abaqus units).
2. Different types of unit systems
Unit systems are essential for maintaining consistency in measurements and calculations. The primary unit systems used are the CGS, FPS, MKS, and SI systems, each with its unique conventions.
CGS System Units: The centimeter-gram-second (CGS) system is a metric system where the centimeter is the unit of length, the gram is the unit of mass, and the second is the unit of time. This system is often used in scientific fields for smaller-scale measurements.
FPS System Units: The foot-pound-second (FPS) system uses feet for length, pounds for mass and force, and seconds for time. Commonly used in the United States, this system is known for its application in engineering and aviation.
MKS System Units: The meter-kilogram-second (MKS) system is another metric system that uses meters for length, kilograms for mass, and seconds for time. This system was foundational in the development of the International System of Units (SI).
SI Units: The International System of Units (SI) is the most widely used and modern metric system. It includes seven base units:
- Ampere (A) for electric current
- Kelvin (K) for temperature
- Second (s) for time
- Meter (m) for length
- Kilogram (kg) for mass
- Candela (cd) for luminous intensity
- Mole (mol) for the amount of substance
These units provide a comprehensive and standardized approach to measurement, facilitating global communication and collaboration in science, engineering, and everyday life.
3. What is the right unit system for our analysis and How to choose it?
Selecting the appropriate unit system in Abaqus (Abaqus units) is crucial for ensuring accurate results and avoiding errors in simulations. Unlike some software, Abaqus does not have a predefined unit system, meaning the user must consistently apply a chosen unit system throughout their analysis. Here’s a simple guide to help you determine the right unit system for your analysis.
3.1. Consistency is Key
The primary rule in Abaqus is consistency. All units for input data must be compatible with each other (Abaqus units). For instance, if you choose to use the metric system with meters (m) for length, you must use compatible units such as kilograms (kg) for mass and seconds (s) for time.
- Example: If a beam is 2 meters long, weighs 50 kilograms, and a force of 100 Newtons is applied, these values fit seamlessly together.
- Example: A small mechanical part with dimensions in centimeters and a mass in grams can be analyzed using this system.
- Example: For precision engineering parts, using millimeters for length and tonnes for mass can be practical.
Using consistent units, you can easily set up your model and ensure that all derived quantities like stress and deformation are accurately calculated.
3.2. Conversion of Units
Sometimes, the data you receive might be in different units. It’s essential to convert all inputs to your chosen unit system. For example, if the density of a material is given in kg/m³ but your length unit is in mm, you must convert the density accordingly to maintain consistency.
Example 1:
Density (SI) = 7800 Kg/m3 Convert it in SI (mm).
Solution:
Note: 1 m = 1000 mm & 1 m3 = 109 mm3
Example 2:
Stress (SI (mm)) = 10 MPa convert it in US Unit (ft).
Solution:
Note:
4. Abaqus Units table
The following table provides examples of consistent systems of units. As points of reference, the mass density and Young’s Modulus of steel are provided in each system of units. “GRAVITY” is the gravitational acceleration.
See the table below as a reference to select consistent units for your problem (Abaqus units):
| Quantity | SI units | ||||||||||
| Mass | kg | ton | kg | kg | kg | kg | g | g | g | g | |
| Length | m | mm | cm | cm | cm | mm | cm | cm | mm | mm | |
| Time | s | s | s | ms | µs | ms | s | µs | s | ms | |
| Force | N | N | 1e-2N | 1e+4N | 1e+10N | kN | dyne | 1e7N | 1e-6N | N | |
| Stress | Pa | MPa | Pa | Pa | Pa | GPa | Dy/cm2 | Mbar | Pa | MPa | |
| Energy | J | N-mm | J | J | J | KN-mm | erg | 1e7N-cm | J | N-mm | |
| Gravity | 9.81 | 9.81e+3 | 9.81e2 | 9.81e-4 | 9.81e-10 | 9.81e-3 | 9.81e+2 | 9.81e-10 | 9.81e+3 | 9.81e-3 | |
| Steel | Density | 7.83e-9 | 7.83e-9 | 7.83e+3 | 7.83e+3 | 7.83e+3 | 7.83e-6 | 7.83 | 7.83 | 7.83e-3 | 7.83e-3 |
| Young Modulus | 2.07e+5 | 2.07e+5 | 2.07e+9 | 2.07e+3 | 2.07e+3 | 2.07e+2 | 2.07e+12 | 2.07 | 2.07e+11 | 2.07e+5 | |
* µs= micro second=10-6 s, ms= millisecond= 10-3 s
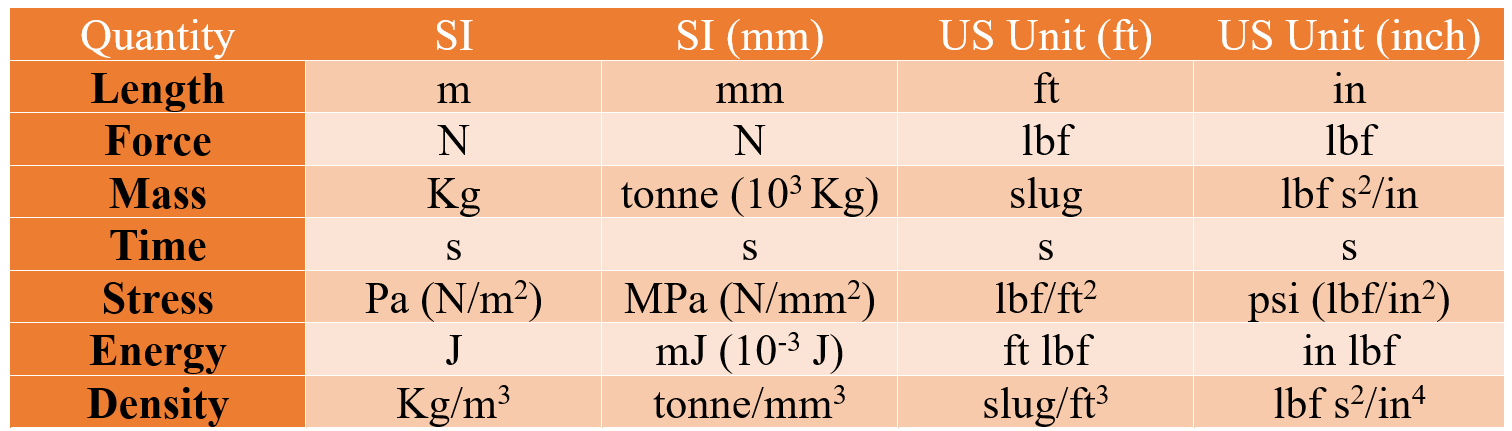
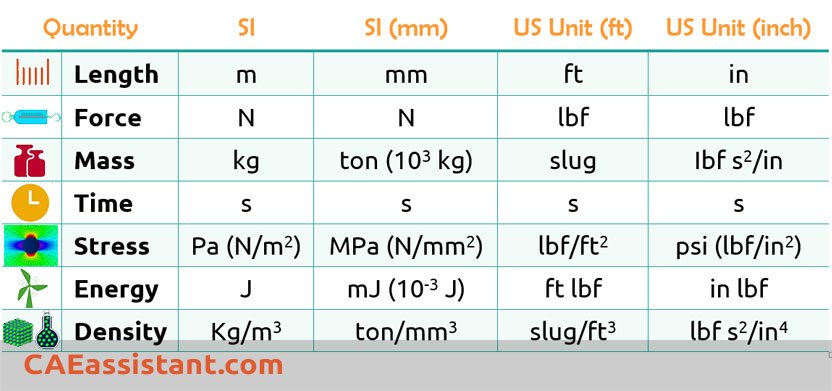
And this (for comparing SI and Imperial units):
5. Tips & Tricks and important notes about Abaqus Units
- Set a Standard: Decide on a unit system before starting your analysis and stick to it throughout the project (Abaqus units).
- Use Abaqus Documentation: Refer to Abaqus documentation for unit guidelines specific to different types of analyses.
- Check Consistency: Regularly verify that all units for input parameters such as material properties, geometry, loads, and boundary conditions are consistent.
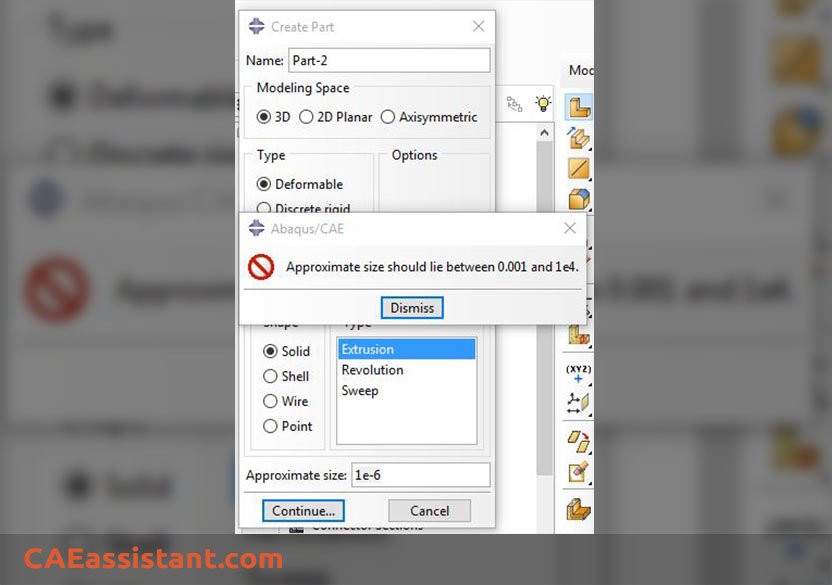
- Modeling sub-micron quantities in Abaqus/CAE is not feasible because of geometric limitations. For instance, a sphere with a radius of 1e-9 cannot be modeled in Abaqus/CAE. Even if it were possible, the analysis would quickly fail due to round-off and truncation errors associated with very small values. Consequently, we must scale down the model and adjust the material properties accordingly.
The naming conventions for imperial (American or English) units are not as clear as those in the SI system, which can lead to confusion. Handbooks often do not specify whether “lb” refers to pound-mass (lbm) or pound-force (lbf). It is essential to ensure that the units used form a consistent set.
For instance, 1 pound-force (lbf) can accelerate 1 pound-mass (lbm) by g ft/sec2, where g represents the acceleration due to gravity. By taking pound-force, feet (ft), and seconds as fundamental units, the derived unit of mass becomes lbf⋅sec2/ft. Since density is typically given in handbooks as lbm/in3, it needs to be converted to lbf⋅sec2/ft4.
Two other units that often cause confusion are the slug and the poundal. A slug is the mass that will accelerate at 1 ft/sec2 with 1 lbf, and a poundal is the force needed to accelerate 1 lbm at 1 ft/sec2. Useful conversions are:
- 1 slug = g×lbm
- 1 lbf = g×poundals
where g is the acceleration due to gravity in ft/sec2.
Choosing units that keep your input values close to 1 can help reduce round-off and truncation errors, improving the accuracy and efficiency of your simulations.
- Abaqus uses radians for rotational degrees of freedom (DOF). However, all other angles, such as those specified in geometry definitions or material properties, are expressed in degrees.
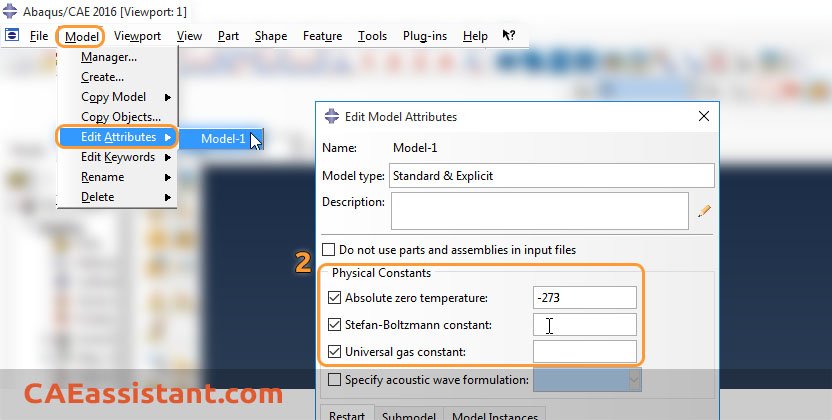
- In heat transfer analyses, when surface emissivity and radiation are involved, the absolute zero temperature and the Stefan-Boltzmann constant must be specified in units consistent with the rest of the model. This requirement also applies to the universal gas constant. These parameters can be set as follows:
[In any Module] Menu Bar > Model > Edit attributes
It would be helpful to see Abaqus Documentation to understand how it would be hard to start an Abaqus simulation without any Abaqus tutorial. Moreover, if you need to get some info about the FEM, visit this article: “Introduction to Finite Element Method | Finite Element Analysis”.
The CAE Assistant is committed to addressing all your CAE needs, and your feedback greatly assists us in achieving this goal. If you have any questions or encounter complications, please feel free to share it with us through our social media accounts including WhatsApp.
6. Conclusion
This article discussed the unit system in Abaqus (Abaqus units), emphasizing that Abaqus does not have a built-in unit system, unlike other software. Instead, users must adopt a self-consistent unit system throughout their modeling process. This approach ensures compatibility among all fundamental and derived units, which is crucial for accurate simulations.
Key topics covered include an overview of different unit systems (CGS, FPS, MKS, SI), guidelines for selecting and converting units, and the importance of maintaining consistency across all input parameters. Understanding these principles is crucial for ensuring accurate simulations in Abaqus, where precise unit alignment directly impacts the reliability and validity of results.