1. Introduction| Abaqus Kelvin Voigt Model (Viscoelastic) Simulation
In this example, we use the UMAT and VUMAT subroutines to simulate the behavior of viscoelastic materials with Abaqus Kelvin Voigt viscoelastic model. That is to say, the geometric model used in this study for the kelvin voigt model Abaqus simulation is a specimen under tension. The behavior of viscoelastic materials is a state between the behavior of a liquid and a solid. In other words, they behave both like liquids and solids. There are many natural and synthetic materials that are classified as viscoelastic materials; From the biological structures of the body such as skin, cartilage and tissue to concrete, foams, rubbers, and synthetic polymers. Due to these unique properties, viscoelastic materials have many applications.
In this regard, the primary goals of this study include the development and implementation of an accurate three-dimensional Abaqus kelvin voigt viscoelastic model, and the integration of viscoelastic properties into the analysis, which can improve the prediction of viscoelastic materials response under different boundary and loading conditions.
This tutorial, by customizing the UMAT and VUMAT subroutines to simulate flexible samples behavior, contributes to the advancement of viscoelastic materials design and analysis.
2. Simulation of the Abaqus kelvin voigt viscoelastic Model using UMAT and VUMAT Subroutines (PDF File)
This project, after teaching the basic fundamentals of material rheological modeling, presents a precise three-dimensional mechanical response of viscoelastic materials using Abaqus kelvin voigt viscoelastic model. We implemented this Abaqus kelvin voigt viscoelastic model with both UMAT and VUMAT subroutines for standard and explicit solvers.
2.1. Problem Description
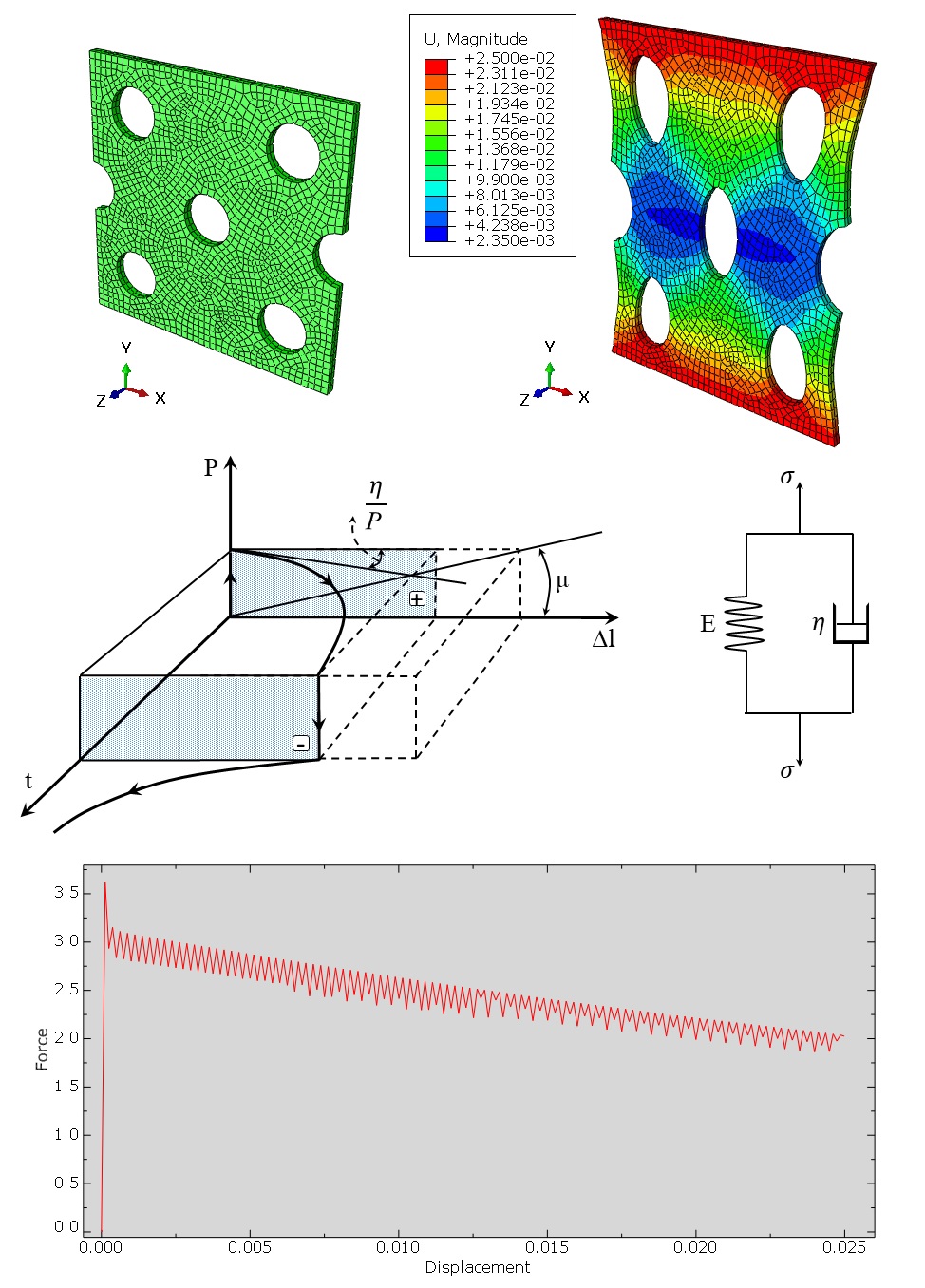
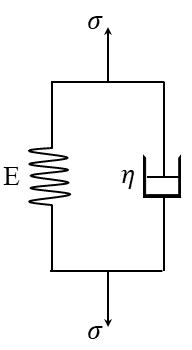
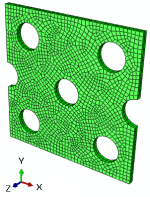
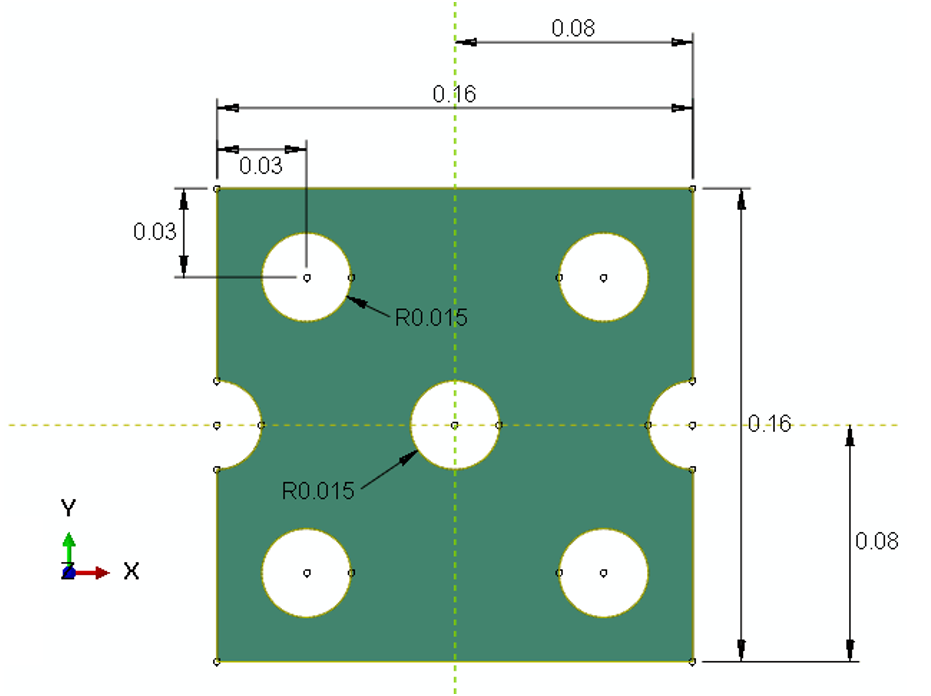
Geometry: This example includes a Lagrangian part that is subjected to tension. To clarify, the schematic design of the part is shown in Figure 1.
The material properties used in this example are presented in an Excel file named “Material Properties”. We import these properties into the UMAT and VUMAT subroutines. That is to say, the materials used in this example are bituminous concrete (asphalt concrete) and epoxy.
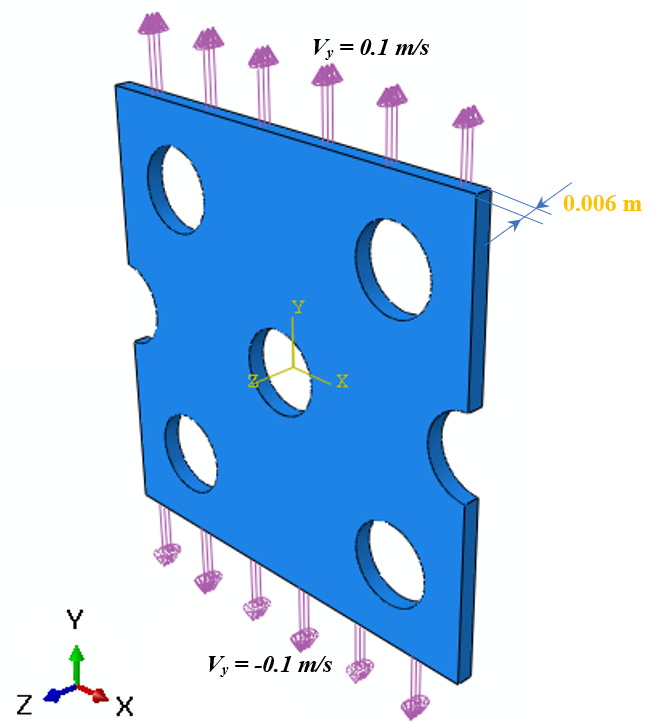
We apply velocity boundary conditions to pull the upper and lower surfaces of the part, as illustrated in Figure 2.
Figure 1: The schematic design of the tensile part
Figure 2: The velocity boundary conditions
2.2. Project procedures
- Setting up the software environment and choosing Abaqus units;
- Creating the tensile part;
- Defining the material properties and creating its relevant section;
- Making an instance of the model in the Assembly module;
- Creating a non-linear “Static, General” step for doing analysis by calling the UMAT subroutine (and a non-linear “Dynamic, Explicit” for doing analysis by calling the VUMAT subroutine);
- Determining the loading and boundary conditions, etc.;
- Generating elements and assigning element types;
- Preparing the UMAT_Kelvin and VUMAT_Kelvin subroutines;
- Creating two job and calling the UMAT and VUMAT subroutines for the relevant job;
- Submitting the jobs;
- Viewing the results.
2.3. Executing Project Procedures
- Setting up the software environment
Geometry:
This example includes a Lagrangian part subjected to tension, with its schematic design shown in Figure 1.
Material Properties:
We present the material properties used in this example in an Excel file named ‘Material Properties.’ We define these properties using the ‘User Material’ option in Abaqus and then import them into the UMAT and VUMAT subroutines.
Steps:
The Analysis procedure for this example would be the non-linear “Static, General” for UMAT_Kelvin subroutine and the non-linear “Dynamic, Explicit” for VUMAT_Kelvin subroutine.
Note: see the attached files (Abaqus model and the UMAT and VUMAT subroutines) to understand the modeling.
Boundary Conditions:
The upper and lower surfaces of the part are pulled using the velocity boundary conditions, as illustrated in Figure 2 (Vy = 0.1 m/s).
Meshing:
For standard solver, the meshing operation was performed using 8-node linear brick elements with “Distortion control” (C3D8) and for explicit solver, the meshing operation was also performed using 8-node linear brick elements (C3D8).
- Preparing the subroutine
All basic concepts of the rheological modeling of materials, especially the Kelvin-Voigt viscoelastic model, are explained in detail in section “Theoretical and Base Relations”. Study this section carefully to understand the UMAT_Kelvin and VUMAT_Kelvin subroutines.
- Creating two job and calling the UMAT and VUMAT subroutines for the relevant job
- Submitting the jobs
- Guidance on how to extract the results
In video file, the process of extracting the results is shown in full details.
2.4. Theoretical and Base Relations
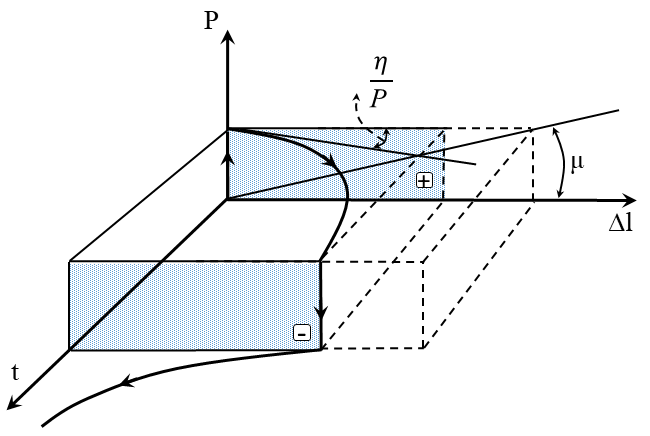
Rheological Modeling of Materials
The term rheology is derived from the Greek word Rheos which means flow. To clarify, rheology is a branch of physics that deals with the deformation and flow of matter and describes the interrelationship of force-deformation-time. As a result, this modeling applies to all materials, from fluids (liquids and gases) to solid materials..
Next, by defining a number of material properties, the elements used in rheological modeling are explained.
Finally, after teaching the basic principles of rheological modeling of materials, an accurate 3D mechanical response of viscoelastic materials is presented using the Abaqus kelvin voigt viscoelastic model. We implement this model using both UMAT and VUMAT subroutines. (for standard and explicit solvers).
- Elastic Property (The Hooke’s element [Symbol H])
- Viscous Properties (The Newtonian element [Symbol N])
- Ideal Rigid-Plastic Materials (The St. Venant element [symbol St V])
- Viscoelastic Materials
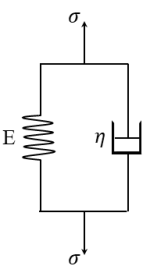
- Kelvin-Voigt Viscoelastic Model
- The Creep-Recovery Response
- The Stress Relaxation
- Maxwell Viscoelastic Model
- The Creep-Recovery Response
- The Stress Relaxation
- Development of the UMAT and VUMAT Subroutines for the Abaqus kelvin voigt viscoelastic model
- The UMAT Subroutine of the Kelvin-Voigt Viscoelastic Model
Presentation and detailed explanation of UMAT subroutine, related to the implementation of the Kelvin-Voigt model for viscoelastic materials.
- The VUMAT Subroutine of the Abaqus kelvin voigt viscoelastic model
Presentation and detailed explanation of VUMAT subroutine, related to the implementation of the Kelvin-Voigt model for viscoelastic materials.
3. Workshop (Video File): A step-by-step guide on Kelvin Voigt model Abaqus simulation
The workshop provides a full step-by-step guide through a video to simplify the simulation of a viscoelastic specimen under tension. That is to say, the Kelvin Voigt model Abaqus anaysis is used to simulate the behavior of the viscoelastic specimen. To clarify, in the video, how to model, call subroutines, submit the jobs and extract results is shown in full detail.
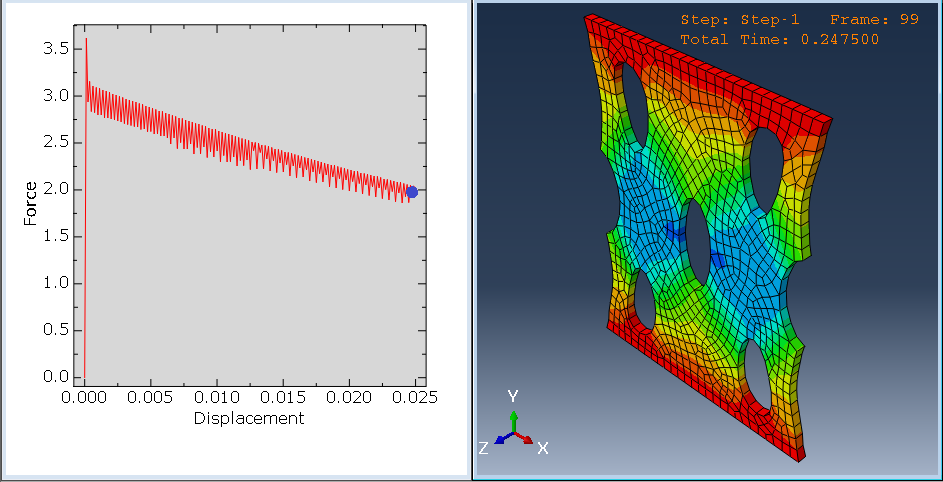
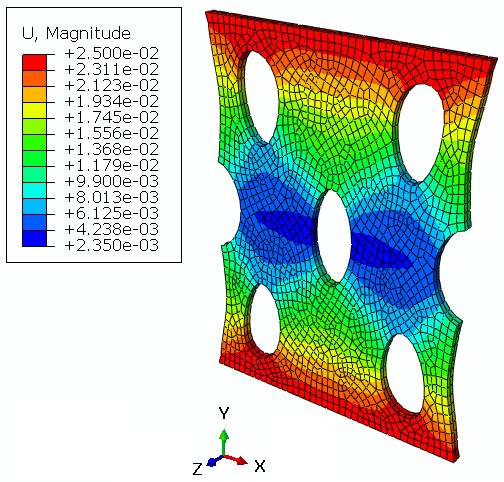
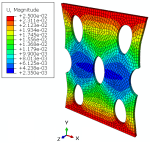
Results
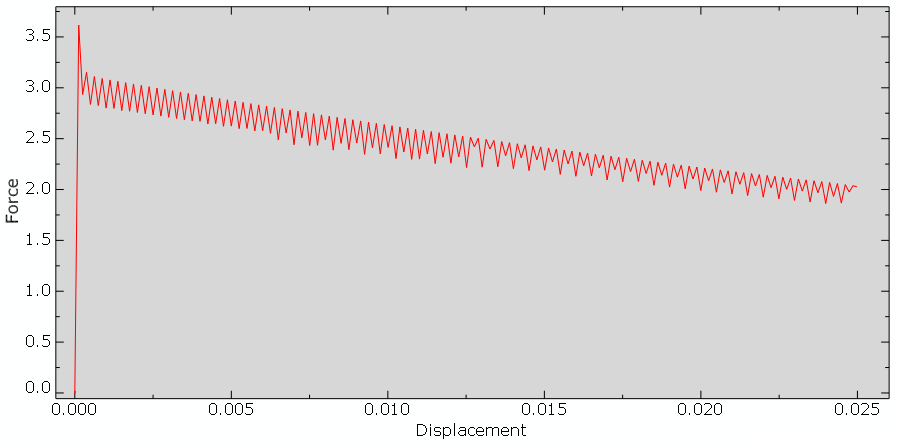
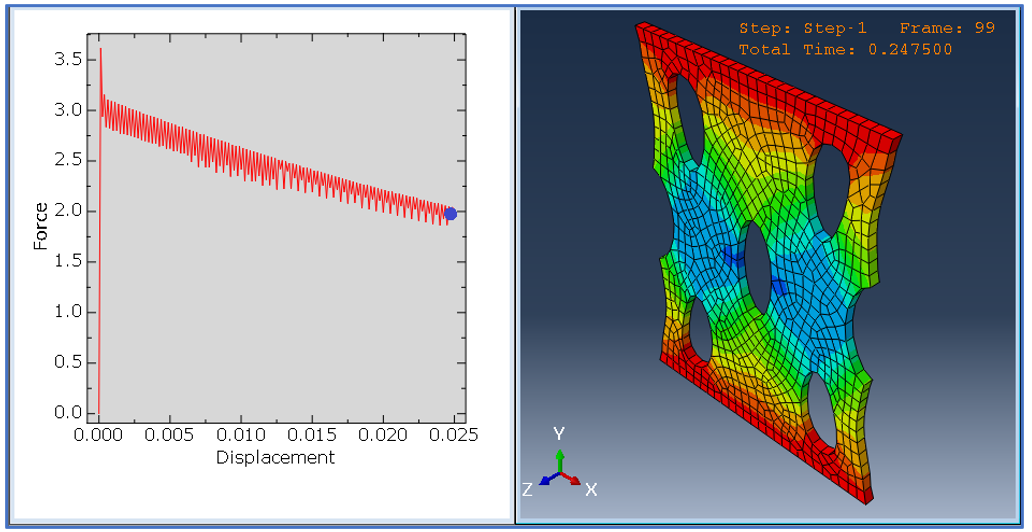
To check the Abaqus kelvin voigt viscoelastic model, we have explored different results in this tutorial. For example, we can refer to the stress distribution field (S), displacement distribution field (U), velocity distribution field (), strain distribution field (), reaction forces (RF), force-displacement diagram (F-U), etc. That is to say, these results are extracted from the analysis to evaluate the material behavior and its performance under different conditions. The results confirm the practicality of kelvin voigt model abaqus simulation.
Figure 3: Force-Displacement diagram
It would be helpful to see Abaqus Documentation to understand how it would be hard to start an Abaqus simulation without any Abaqus tutorial.
One note, when you are simulating in Abaqus, be careful with the units of values you insert in Abaqus. Yes! Abaqus don’t have units but the values you enter must have consistent units. You can learn more about the system of units in Abaqus.














Reviews
There are no reviews yet