Abaqus Kelvin Voigt Model (Viscoelastic) Simulation Using UMAT and VUMAT Subroutines
This research presents a precise three-dimensional mechanical response of viscoelastic materials using Abaqus kelvin voigt viscoelastic model. We performed this kelvin voigt model Abaqus simulation using both UMAT and VUMAT subroutines for standard and explicit solvers.
The behavior of viscoelastic materials is a state between the behavior of a liquid and a solid. In other words, they behave both like liquids and solids. That is to say, there are many natural and synthetic materials that are classified as viscoelastic materials; From the biological structures of the body such as skin, cartilage and tissue to concrete, foams, rubbers, and synthetic polymers. Due to these unique properties, viscoelastic materials have many applications.
In this regard, the primary goals of this study include the development and implementation of an accurate three-dimensional Abaqus kelvin voigt viscoelastic model, and the integration of viscoelastic properties into the analysis, which can improve the prediction of viscoelastic materials response under different boundary and loading conditions.
This tutorial, by customizing the UMAT and VUMAT subroutines to simulate flexible samples behavior, contributes to the advancement of viscoelastic materials design and analysis.
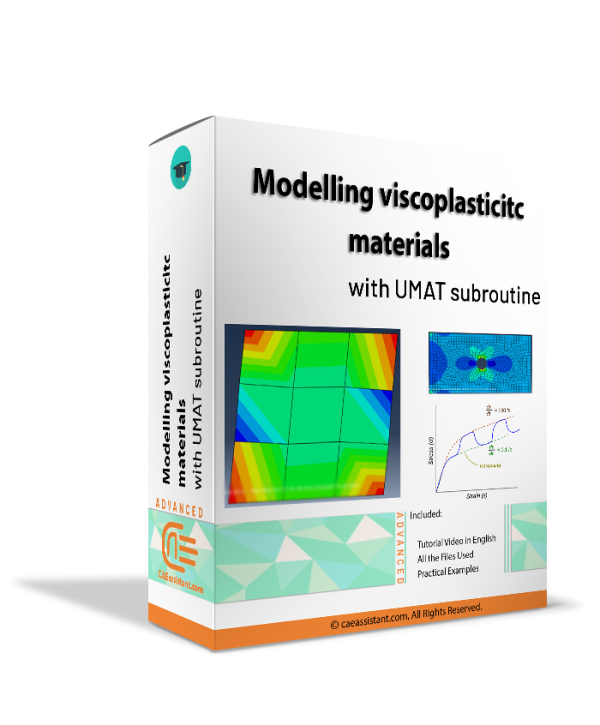
Viscoplasticity Abaqus Simulation Using UMAT Subroutine | Perzyna Viscoplastic Model
Viscoplasticity describes the rate-dependent inelastic behavior of materials, where deformation depends on both stress magnitude and application speed. This concept is crucial in many engineering applications, such as designing structures under dynamic loads, modeling soil behavior during earthquakes, and developing materials with specific mechanical properties. Viscoplasticity Abaqus simulation, especially using Abaqus with UMAT subroutines, are vital for understanding, predicting, and optimizing the behavior of viscoplastic materials. This tutorial focuses on implementing the Perzyna viscoplasticity model in Abaqus. The Perzyna viscoplastic model, a strain rate-dependent viscoplasticity model, relates stress to strain through specific constitutive relations. This involves defining plastic strain rate based on stress state, internal variables, and relaxation time. The tutorial provides general UMAT codes for viscoplastic analysis, yielding results like stress fields essential for various engineering applications. These simulations help in predicting permanent deformations, assessing structural failure points, and analyzing stability under different loads, benefiting fields such as aerospace, automotive, civil engineering, and energy.
Pultrusion Crack Simulation in Large-Size Profiles | Pultrusion Abaqus
Pultrusion is a crucial task for producing constant-profile composites by pulling fibers through a resin bath and heated die. Simulations play a vital role in optimizing parameters like pulling speed and die temperature to enhance product quality and efficiency. They predict material property changes and aid in process control, reducing reliance on extensive experimental trials. However, simulations face challenges such as accurately modeling complex material behaviors and requiring significant computational resources. These challenges underscore the need for precise simulation methods to improve Pultrusion processes. This study employs ABAQUS with user subroutines for detailed mechanical behavior simulations, including curing kinetics and resin properties. Key findings include insights into crack formation (pultrusion crack simulation), material property changes, and optimization strategies for enhancing manufacturing efficiency and product quality. This research (pultrusion Abaqus) provides practical knowledge for implementing findings in real-world applications, advancing composite material production.
Elastomeric Foam Simulation Using Abaqus Subroutines
Abaqus convergence tutorial | Introduction to Nonlinearity and Convergence in ABAQUS
This package introduces nonlinear problems and convergence issues in Abaqus. Solution convergence in Abaqus refers to the process of refining the numerical solution until it reaches a stable and accurate state. Convergence is of great importance especially when your problem is nonlinear; So, the analyst must know the different sources of nonlinearity and then can decide how to handle the nonlinearity to make solution convergence. Sometimes the linear approximation can be useful, otherwise implementing the different numerical techniques may lead to convergence.
Through this tutorial, different nonlinearity sources are introduced and the difference between linear and nonlinear problems is discussed. With this knowledge, you can decide whether you can use linear approximation for your nonlinear problem or not. Moreover, you will understand the different numerical techniques which are used to solve nonlinear problems such as Newton-Raphson.
All of the theories in this package are implemented in two practical workshops. These workshops include modeling nonlinear behavior in Abaqus and its convergence study and checking different numerical techniques convergence behavior using both as-built material in Abaqus/CAE and UMAT subroutine.