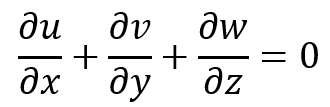The Guide for Porous Media Flow

Porous media flow is a critical aspect of fluid dynamics, involving the movement of fluids through porous materials. This blog explores its importance in various fields, including hydrology, petroleum engineering, soil science, and chemical engineering. By examining models like Darcy’s Law, Forchheimer’s Law, and the Richards Equation, we provide a clear understanding of how single-phase fluid flow is described under different conditions.
We also present a practical example using extended Darcy’s law in a photovoltaic system cooler simulation. Through advanced numerical methods in ANSYS Fluent, we demonstrate key steps such as mesh generation, boundary condition setup, and equation solving. Readers will learn about optimizing the thermal efficiency of photovoltaic modules and gain insights into the practical applications of porous media flow models. This blog is a valuable resource for anyone interested in fluid dynamics and its applications.
1. Introducing Porous Media Flow
One of the interesting fields of fluid dynamics is porous media flow. Porous media flow refers to the movement of fluids (liquids or gases) through a porous material. This type of flow is characterized by the fluid moving through the interconnected pore spaces within the material. Porous media flow is an important concept in various fields, including hydrology, petroleum engineering, soil science, and chemical engineering.
Porous media flow modeling is a branch of fluid dynamics that deals with the movement of fluids (liquids or gases) through porous materials such as soil, rocks, or biological tissues. It finds applications in various fields including hydrogeology, petroleum engineering, environmental science, soil mechanics, and bioengineering.
2. Studying Porous Media Flow
There are several mathematical models used to describe fluid flow in porous media. We assume a single-phase fluid flow here. Some of the commonly employed models for a single-phase flow include:
- Darcy’s Law: Darcy’s Law is a classical model that describes the flow of a single-phase fluid through a porous medium under steady-state conditions. It relates the fluid velocity to the pressure gradient and the medium’s permeability.
- Forchheimer’s Law: Forchheimer’s Law is an extension of Darcy’s Law, which accounts for the inertial effects at high flow velocities or in non-viscous fluids. It includes an additional quadratic term proportional to the square of the fluid velocity.
- Dupuit-Forchheimer Approximation: This model is a combination of Darcy’s Law and Forchheimer’s Law, often used to describe flow in porous media where both viscous and inertial effects are significant.
- Extended Darcy’s Law: Extended Darcy’s Law incorporates additional terms to account for non-Darcian effects such as gravity, capillarity, or spatial heterogeneity in the porous medium.
- Richards Equation: The Richards equation is a partial differential equation commonly used to model the flow of water in unsaturated porous media. It accounts for the effects of gravity, capillarity, and water retention characteristics of the soil.
- Nonlinear Diffusion Equation: This model is derived from the conservation of mass principle and describes the transient flow of a single-phase fluid in porous media, considering the effects of diffusion, advection, and storage.
- Buckley-Leverett Equation: The Buckley-Leverett equation is used to model the immiscible displacement of one fluid by another in porous media, typically encountered in enhanced oil recovery processes.
- Porous Media Equations in Computational Fluid Dynamics (CFD): In computational fluid dynamics simulations, various numerical methods are used to solve the governing equations of fluid flow in porous media, often based on the Navier-Stokes equations or variants tailored for porous media.
These models may vary in complexity and applicability depending on factors such as the characteristics of the porous medium, the nature of the fluid flow (steady-state or transient), and the specific phenomena being studied (e.g., advection, diffusion, dispersion, or reaction). Choosing the appropriate model depends on the specific requirements and objectives of the study or application.
The fundamental principle in this field is Darcy’s law governing fluid flow through porous media. It states that the velocity of fluid flow is directly proportional to the pressure gradient and inversely proportional to the viscosity and the permeability of the porous medium. However, this equation has several limitations and cannot solve every problem.
Extended Darcy’s Law is a modification of the classical Darcy’s Law that incorporates additional terms to account for non-Darcian effects such as gravitational forces, capillary effects, or spatial heterogeneity in the porous medium. It provides a more comprehensive description of fluid flow in porous media under conditions where the assumptions of Darcy’s Law may not hold.
3. Example of Porous Media Flow Modeling
The topic would be more understandable if we take a look at an example. As mentioned Darcy’s law has many limitations so Hakeem et al, modeled water flow in a PV system cooler governed by the extended form of Dracy’s law. They did a numerical simulation using ANSYS based on the following steps:
To perform a numerical simulation based on the information provided in the paper, follow these steps:
- Mesh Generation:
– Create a mesh for the PV panel chamber with 605,071 nodes and 3,588,460 elements to ensure stability and grid independence.
- Boundary Conditions:
– Set the inlet flow to be uniform at a constant temperature of 298K.
- Solving Equations:
– Solve the equations of continuity, momentum, and energy.
– Ensure that the residual value for all equations is below 10-7.
- Advection Scheme:
– Use a 2nd order high-resolution advection scheme for high accuracy.
- Assumptions:
– Assume the transmissivity of ethyl vinyl acetate (EVA) is approximately 100%.
– Assume no dust on the top surface, so solar energy absorptivity is unaffected.
– Assume the water flow is steady, laminar, and incompressible.
– Assume the porous medium is uniform, rigid, isotropic, and fully saturated with water.
– Consider single-phase flow.
- Modeling the Cooling Chamber:
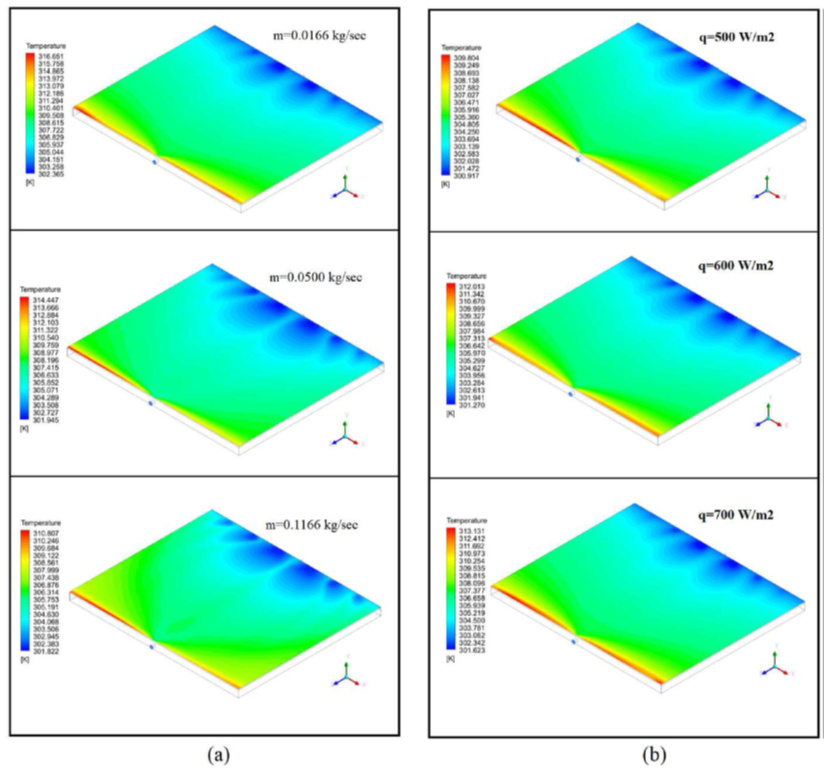
– Develop a geometric model of the PV panel with a cooling chamber using three different diameters (6, 11, 16 mm) of plastic porous media with the same thermal conductivity.
– Investigate the influences of flow rate, porosity, and radiation intensity to achieve high thermal efficiency.
- Software:
– Use ANSYS Fluent for numerical modeling and simulations.
- Validation:
– Compare the numerical results with experimental data to ensure accuracy, noting that the variance may be due to environmental factors like airflow and dust.
Governing equations for an incompressible, laminar flow are:
And or the effective thermal conductivity is:
In which, and
are stagnant thermal conductivity and thermal dispersion conductivity, respectively.
By following the above steps, you can replicate the numerical simulation described in the paper to study the effects of cooling techniques on the efficiency of a photovoltaic module. You can see the results in the figure below:
4. Conclusion
Porous media flow is a cornerstone of fluid dynamics, with broad applications across various scientific and engineering fields. Through this blog, we’ve explored essential models such as Darcy’s Law, Forchheimer’s Law, and the Richards Equation, providing a comprehensive understanding of how single-phase fluid flow is described in porous materials. These models help address various flow conditions and the specific phenomena involved, offering valuable insights into hydrology, petroleum engineering, soil science, and chemical engineering.
The practical example of a photovoltaic system cooler simulation using extended Darcy’s law illustrates the importance of numerical methods in real-world applications. By detailing the steps in ANSYS Fluent, from mesh generation to solving equations, we’ve shown how to enhance the thermal efficiency of photovoltaic modules. This blog has offered both theoretical knowledge and practical applications, serving as a useful guide for those interested in fluid dynamics and its impact on various industries.
Explore our comprehensive Abaqus tutorial page, featuring free PDF guides and detailed videos for all skill levels. Discover both free and premium packages, along with essential information to master Abaqus efficiently. Start your journey with our Abaqus tutorial now!