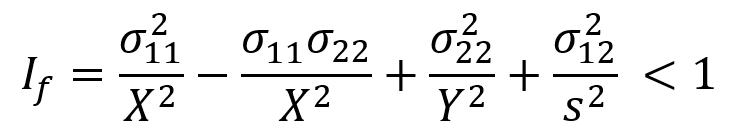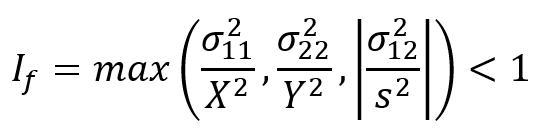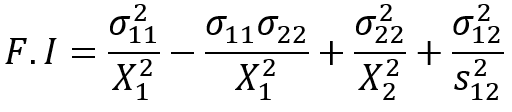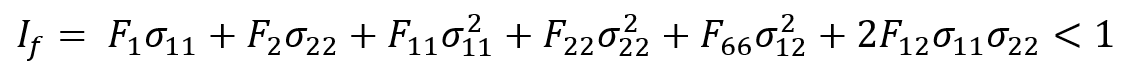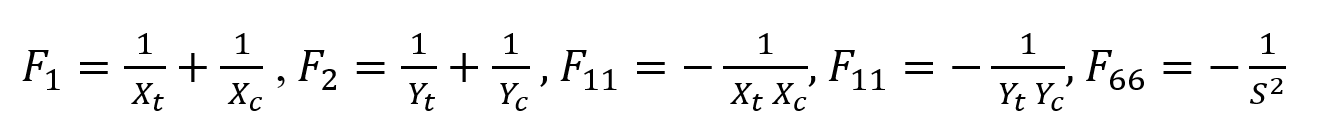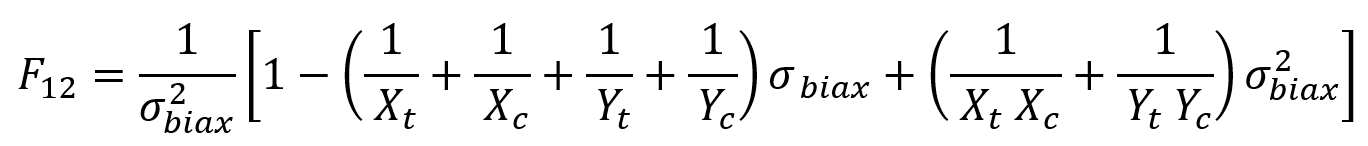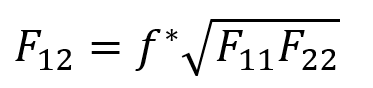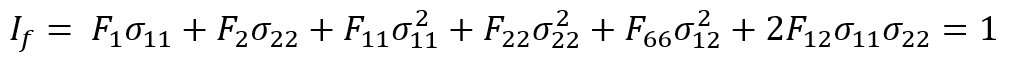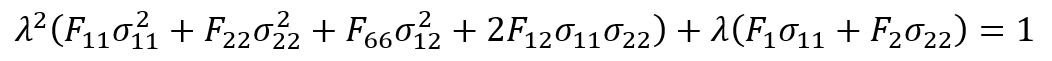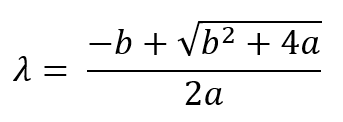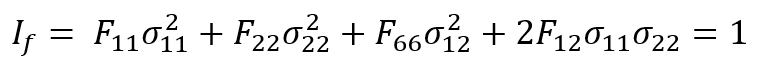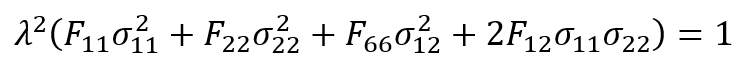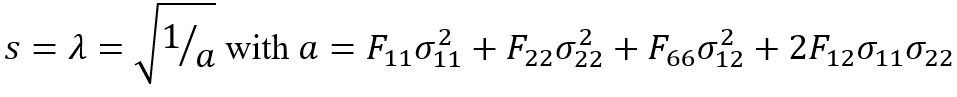When working with composite materials, predicting how they will perform under stress is crucial. This is where failure criteria like the Tsai Hill failure criterion and Tsai Wu failure criterion come into play. These criteria help engineers and researchers determine when a composite material will fail, ensuring that designs are both safe and efficient. Understanding these criteria is essential for applications in aerospace, automotive, and other high-performance industries.
The Tsai-Hill and Tsai-Wu failure criteria offer different approaches to analyzing composite materials. The Tsai-Hill criterion extends the von Mises yield criterion to account for the unique properties of composites, providing a simplified yet effective method for predicting failure. On the other hand, the Tsai-Wu criterion adds more detail by incorporating both quadratic and linear terms, allowing for a more comprehensive analysis of materials under complex stress conditions. The main difference lies in how these criteria handle multi-axial stresses and the additional factors considered.
In this blog, we will explore both the Tsai-Hill and Tsai-Wu failure criteria in detail. We will begin by introducing each criterion and explaining their applications and differences. Then, we’ll delve into their practical use in industries and how they are implemented in software like Abaqus. By the end, you’ll have a clear understanding of these criteria and how they can be applied to ensure the reliability of composite materials in various engineering contexts.
1. What is the Tsai Hill Failure Criterion?
The Tsai Hill failure criterion, developed by Stephen W. Tsai and adapted from the Hill yield criterion for anisotropic materials, is an important theoretical framework for predicting the failure of composite materials. This criterion extends the von Mises yield criterion, originally used for isotropic materials, to accommodate the anisotropic properties of composites. The Tsai Hill failure criterion provides a simplified yet effective method for assessing the strength and failure potential of composite materials under various loading conditions.
The Tsai-Hill criterion is observed to be homogeneous, meaning it does not include linear terms in its formulation. In the context of failure criteria, a homogeneous criterion implies that the failure index is expressed as a function of the squares of the stress ratios rather than linear combinations of the stress components. This is significant because:
Quadratic Form: The absence of linear terms indicates that the failure criterion is represented in a quadratic form. This means that the relationship between the stresses and the failure condition is more complex and can capture interactions between different stress components.
Predictive Capability: Homogeneous criteria like the Tsai Hill failure criterion can provide a more accurate prediction of failure under multi-axial loading conditions, as they consider the combined effects of different stress states without introducing additional linear dependencies.
Comparison with Inhomogeneous Criteria: In contrast, inhomogeneous criteria (like the Tsai Wu failure criterion) include both quadratic and linear terms, which can lead to different predictions of failure depending on the loading conditions and material properties. The presence of linear terms can make the results more sensitive to the specific loading scenario.
The plastic potential or yield criterion takes the form:
F, O, H, L, M, N are constants characteristic of the current state of anisotropy. The expression for only has this form when the principal axes of anisotropy are chosen as axes of reference. The input data for the stress-based failure theories are tensile and compressive stress limits, 
and 
, in the 1-direction; tensile and compressive stress limits, 
and 
, in the 2-direction; and shear strength (maximum shear stress), S, in the X–Y plane.
1.1. Tsai-Hill VS Maximum Stress
The Tsai Hill failure criterion is expressed in terms of the material’s strength parameters and applied stress components. It combines these stresses to form an equivalent stress measure that, when it exceeds a certain limit, indicates material failure. The general form of the Tsai Hill failure criterion after simplifying the above equation can be written as follows:
If 
; otherwise, 
. If 
; otherwise, 
.
where:
-
and 
are the normal stresses in the principal material directions, 
is the shear stress,- X and Y are the material strengths in the principal directions,
- S is the shear strength of the material.
and 
are the normal stresses in the principal material directions,
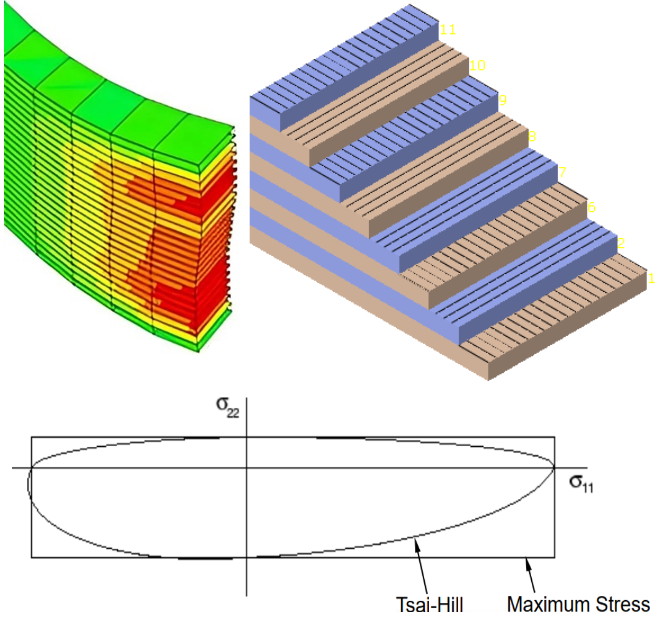
is the shear stress,To illustrate stress-based failure measures picture below is shown. This is a piecewise-continuous failure surface.
Figure 1: Tsai-Hill VS Maximum Stress
Where Maximum stress failure is:
Overall, the homogeneity of the Tsai-Hill criterion simplifies its application in design and analysis, as it focuses on the quadratic interactions of stress components, making it easier to use in practical engineering scenarios.
 |
In this Abaqus training package for beginners, which is designed for FEM Simulation students in mechanical engineering, various examples in the most widely used fields are presented:
|
1.2. Tsai-Hill in Composite Shells
The Tsai-Hill criterion is particularly useful for composite materials, such as composite shells. It specifically addresses the distortion energy portion of the total strain energy that is stored under loading. Distortion energy leads to shape change, whereas dilatation energy causes a change in volume or area (in 2D materials).
For composite shells—like laminae, where σ3=0, τ13=0, τ23=0 the failure index is calculated by considering both the tensile and compressive strengths of the laminate in different material directions:
- is the tensile strength in material direction 1,
- X2 is the tensile strength in material direction 2,
- S12 is the shear strength.
The factor of safety (FOS) is computed as , where F.I is the failure index. A FOS greater than 1 means the laminate is safe from failure, while a value of 1 indicates imminent failure.
For tensile stresses in direction 1:
- if σ1>0,
- X1=X1C if σ1<0.
Similarly, for direction 2:
- X2=X2T if σ2>0,
- X2=X2C if σ2<0.
This interactive failure theory takes into account the interplay between stress components, making it more accurate for predicting composite material failure under varied loading conditions.
1.3. Limitation of Tsai-Hill Failure Criterion
Despite its usefulness, the Tsai-Hill failure criterion has some limitations. It does not predict different failure modes such as:
- Fiber failure,
- Matrix failure, or
- Fiber-matrix interface failure.
This can limit its application in cases where understanding specific failure mechanisms is critical.
2. What is the Tsai Wu Failure Criterion?
The Tsai Wu Failure Criterion is a critical tool in the field of composite material analysis. Developed from the pioneering work of Hill, Tsai, and Wu, this criterion provides a theoretical framework for predicting the failure of composite materials under various loading conditions. By extending the von Mises yield criterion used for isotropic materials, the Tsai Wu failure criterion accommodates the anisotropic properties of composites, making it a powerful method for engineers and researchers. In this blog, we will explore the fundamentals of the Tsai-Wu criterion, compare it with the Tsai-Hill model, and discuss the advancements made in its application.
The Tsai-Wu theory is expressed as a quadratic function of the ratios of applied stresses to the material’s allowable stresses. This criterion combines different stress components into an invariant formula that predicts failure when the calculated value reaches or exceeds a set threshold, typically one. The general form of the Tsai-Wu failure criterion is as follows:
where:
- and are the normal stresses in the principal material directions,
is the shear stress,-
are material coefficients determined experimentally.
is the shear stress,
are material coefficients determined experimentally.The Tsai-Wu coefficients are defined:
is the equibiaxial stress at failure. If is given:
otherwise,
Where: 
and the 
default value of is zero.
These coefficients are defined based on the material’s properties, such as tensile and compressive strengths, and are crucial for accurate failure predictions.
2.1. Improvements in the Tsai-Wu Criterion
The original Tsai Wu failure criterion has been improved to make it more accurate, especially under complex stress conditions. Some of the key improvements include:
- Distinguishing Between Failure Modes: The updated criterion can tell the difference between various failure modes by using different values for the material coefficients. This is important because composite materials can fail in different ways depending on the stresses they are under.
- Analyzing Stiffness Reduction: The improved version can also analyze how the stiffness of composite materials decreases as they become damaged. This helps in understanding how the material’s properties change as it gets closer to failure.
- Considering Hydrostatic Pressure: Unlike the original criterion, the improved Tsai-Wu model takes into account the effects of hydrostatic pressure on the in-plane shear strength of materials. It suggests that increased hydrostatic pressure can actually increase shear strength, rather than causing immediate failure.
2.2. How to use Tsai-Wu Criteria in laminate composites
The Tsai-Wu failure criterion for a lamina is used to predict failure in composite materials, particularly in unidirectional fiber-reinforced laminates. The criterion is formulated to account for the interactions between different stress components in the lamina.
For a given lamina stress field σ in material coordinates, the criterion can also be represented using a safety factor s, which is equivalent to the scalar load multiplier λ that indicates the onset of failure. This allows us to express σ as:
The inhomogeneous Tsai–Wu criterion is now written as:
By solving the λ equation, it is defined as follows:
With a is 
and b is 
.
The Tsai-Hill criterion is simpler than the Tsai-Wu criterion, but it does not account for the significant differences between compressive and tensile strength found in modern composite materials.
Expressing the criterion in terms of the scalar load multiplier λ at failure is straightforward and yields an expression that is comparable to, if not simpler and more homogeneous than, the Tsai-Wu criterion. So:
Where
 |
⭐⭐⭐Free Abaqus Course | ⏰10 hours Video 👩🎓+1000 Students ♾️ Lifetime Access
✅ Module by Module Training ✅ Standard/Explicit Analyses Tutorial ✅ Subroutines (UMAT) Training … ✅ Python Scripting Lesson & Examples |
3. Tsai-Hill vs. Tsai-Wu Failure Criteria
One of the key distinctions between the Tsai-Wu and Tsai-Hill criteria is their approach to handling multi-dimensional and multi-axial stresses. While the Tsai-Hill criterion provides a simplified approach by assuming the material’s isotropic behavior, the Tsai-Wu criterion offers a more comprehensive analysis by allowing the transformation of stress components to align with the material’s symmetry axes. This makes the Tsai-Wu criterion particularly useful for analyzing the strength of anisotropic materials, such as composites, under complex loading conditions.
The Tsai-Wu criterion also introduces more terms in its formulation compared to the standard Tsai-Hill model, allowing it to address additional stress components, which is especially important in configurations involving transverse isotropy.
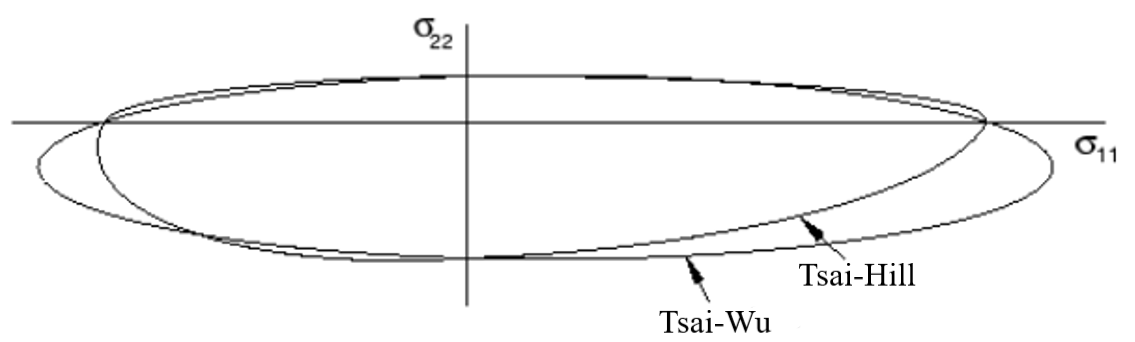
If 
equals zero, the Tsai-Wu model looks as follows when compared to the Tsia-Hill Tsai-Hill model:
Figure 2: Tsai-Wu VS Tsai-Hill
Both the Tsai-Wu and Tsai-Hill criteria are valuable tools in designing composite laminates, but they serve different purposes:
- Tsai-Wu Criterion: This method is more versatile and can adapt to different stress conditions, making it ideal for complex applications where the material properties and loading conditions vary.
- Tsai-Hill Criterion: This simpler method is easier to use, particularly when the material’s compressive and tensile strengths are similar. However, it may not be as accurate in situations where these strengths differ significantly.
4. Where Are These Criteria Used?
The Tsai-Wu and Tsai-Hill theories are especially effective in predicting failure in laminate composites, such as those used in unidirectional fiber-reinforced laminates. These laminates are widely used in industries where materials need to be both strong and lightweight. Here’s how these theories are applied in various fields:
- Aerospace: Aircraft components made from composites need to withstand various forces. The Tsai-Wu and Tsai-Hill criteria help ensure that these parts can handle the stress without failing, making them vital in the design of wings, fuselages, and more.
- Automotive: In cars, especially high-performance vehicles, lightweight yet strong materials are essential. These failure criteria help in designing components that are durable enough to protect passengers in the event of a crash while keeping the vehicle lightweight for better performance.
- Sports Equipment: From tennis rackets to bicycle frames, sports equipment needs to endure high levels of stress during use. The Tsai-Wu and Tsai-Hill theories help manufacturers design gear that can handle intense pressure without breaking, ensuring both safety and performance.
5. Tsai-Wu and Tsai-Hill Criteria in Abaqus
ABAQUS provides a damage model that allows for predicting the onset of damage and simulating damage evolution in elastic-brittle materials with anisotropic behavior. This model is mainly designed for use with fiber-reinforced materials, which commonly display these characteristics.
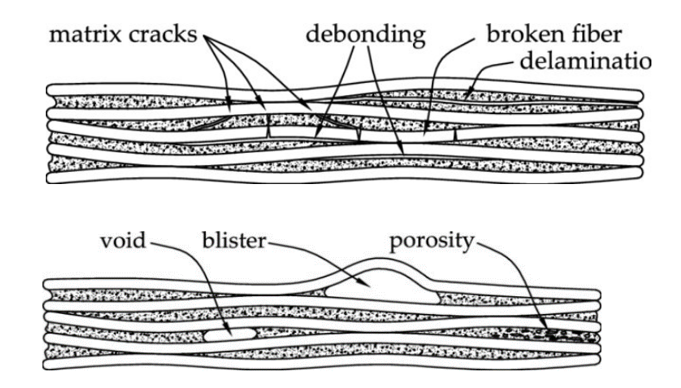
Ply failure is related to membrane and bending stresses and depends on the loading conditions and the orientation of the reinforcement. Delamination is linked to the presence of transverse shear stresses. Consequently, the initial failure might not occur in one of the outermost layers, requiring all layers to be monitored for failure. Ply failure can result from any or all of the following modes: fiber tension, fiber compression, matrix tension, and matrix compression.
Figure 3: Damage mechanisms [Ref]
As we mentioned earlier, ply failure in laminated composites is closely related to the stresses that occur both within the plane (membrane stresses) and due to bending. How and when these failures happen depend on the loading conditions and the orientation of the reinforcement fibers. Delamination, on the other hand, is typically caused by transverse shear stresses.
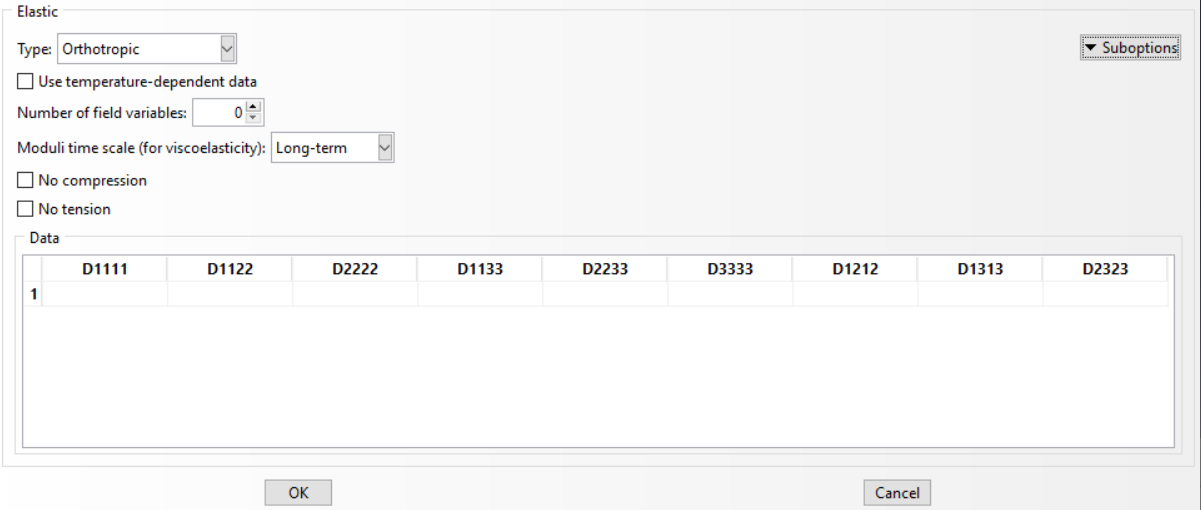
The in-plane failure mode is influenced by the direction and sign of the stresses and strains relative to the reinforcement direction. This means that the first signs of failure might not always show up in the outermost layers of the laminate. To catch any issues early, it’s essential to monitor all layers for potential failure. In Abaqus properties, failure criteria are defined as suboptions of the elastic material properties.
Figure 4: Define Failure criteria
Where whose parameters are composite stiffness tensors for plane stress.
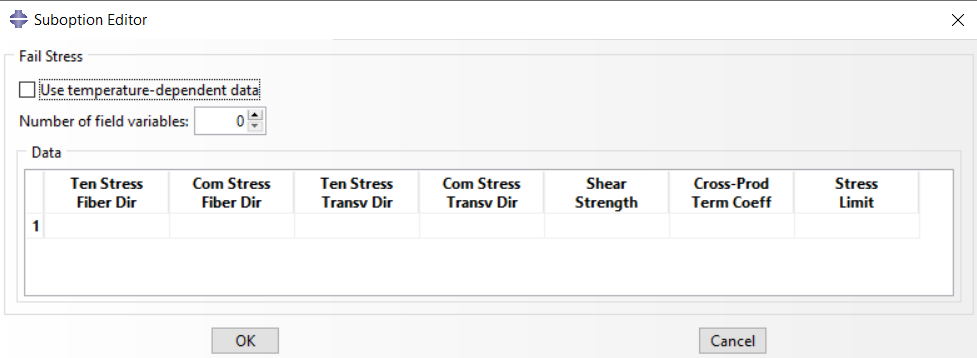
as seen in the picture below, the stress-based failure option outlines the tensile and compressive stress limits for both the 1- and 2-directions, the shear strength in the 1-2 plane, a scaling factor for the Tsai-Wu coefficient 
when no biaxial stress limit is specified, and the biaxial stress limit.
Figure 5: Define damage parameters
Where the parameters from left to right are 
and .
Here, we have two interesting packages that include practical examples related to the Tsai-Hill and Tsai-Wu criteria. One focuses on composite pressure vessels, while the other is designed for unidirectional composites.
 |
|
 |
|
6. Conclusion
In this article, we explored the Tsai Wu failure criterion and Tsai Hill failure criterion, two essential models for predicting the failure of composite materials under stress. These criteria play a critical role in the design and analysis of composite structures, ensuring their reliability and safety across various applications.
Accurate failure prediction is crucial, especially as composite materials become increasingly prevalent in industries such as aerospace, automotive, and civil engineering due to their high strength-to-weight ratio. We provided a detailed comparison of the Tsai-Hill and Tsai-Wu criteria, beginning with the Tsai Hill failure criterion, which simplifies failure prediction by adapting the von Mises criterion to anisotropic materials. This criterion is particularly useful for handling multi-axial stress without the need for additional linear dependencies, making it practical for many engineering applications. However, we also highlighted its limitations when dealing with more complex stress states.
We then delved into the Tsai Wu failure criterion, which offers a more comprehensive approach by incorporating both quadratic and linear terms. This allows for a more accurate evaluation of multi-axial stress states and accounts for material symmetry axes, making it more suitable for detailed and critical applications. Additionally, we discussed an improved version of the Tsai-Wu criterion that distinguishes between different failure modes and includes considerations like stiffness reduction and hydrostatic pressure, further enhancing its predictive accuracy.
In wrapping up, while the Tsai Hill failure criterion offers simplicity and practicality, the Tsai Wu failure criterion provides a higher degree of precision, making it the better choice for complex and critical engineering applications. By understanding these differences, engineers can select the most appropriate failure model to optimize laminate designs and ensure the safety and performance of advanced composite structures.
Explore our comprehensive Abaqus tutorial page, featuring free PDF guides and detailed videos for all skill levels. Discover both free and premium packages, along with essential information to master Abaqus efficiently. Start your journey with our Abaqus tutorial now!
The CAE Assistant is committed to addressing all your CAE needs, and your feedback greatly assists us in achieving this goal. If you have any questions or encounter complications, please feel free to share it with us through our social media accounts including WhatsApp.
Of course you can always learn more in detail about Abaqus in Abaqus Documentation.