In Detail: Material Damping Abaqus🔍 | Rayleigh, Structural, and Viscoelastic Damping
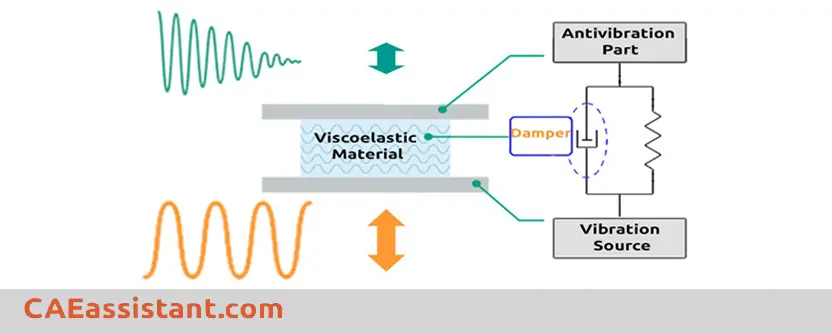
1. An Introduction to Abaqus Damping
What is Abaqus damping, and why is it important?This passage delves into the world of Abaqus damping, with a particular focus on material damping Abaqus, Rayleigh damping Abaqus, structural damping Abaqus, and Abaqus global damping. Damping in Abaqus is a vital concept, aimed at reducing or controlling movement in dynamic systems. It finds application in various scenarios, including viscoelastic Abaqus, where the Prony series Abaqus formulation is employed. Material damping Abaqus is explored in depth, covering its use in both direct-integration and mode-based dynamic analyses. Structural damping in Abaqus is discussed, emphasizing its suitability for models involving frictional behavior or local friction effects. Abaqus global damping is presented as a way to improve performance in preliminary design. This passage offers valuable insights for those seeking to understand and apply Abaqus damping techniques and includes references to Abaqus viscoelastic tutorials for further learning.
As mentioned above, damping is an influence within or upon a dynamic system that has the effect of reducing, restricting, or preventing its movements. In physical systems, damping is produced by processes that dissipate energy. Damping forces come from several sources simultaneously, such as energy loss during hysteretic loading, viscoelastic material properties, contact friction and so on. If would like to know more about the basic concepts of damping, you can simply click on “what-is-damping?“
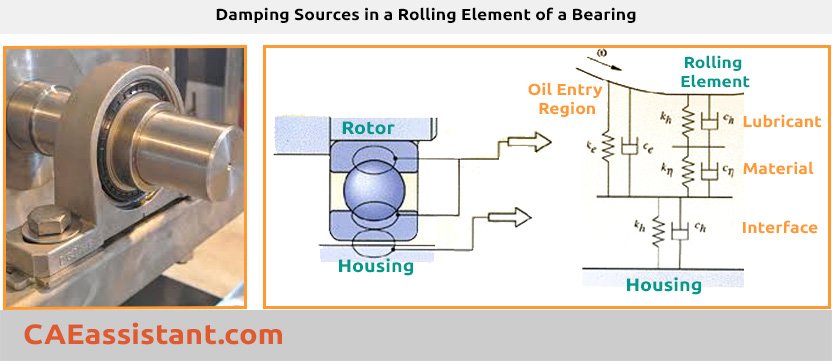
Damping in a rolling bearing [Ref]
2. Sources of Damping
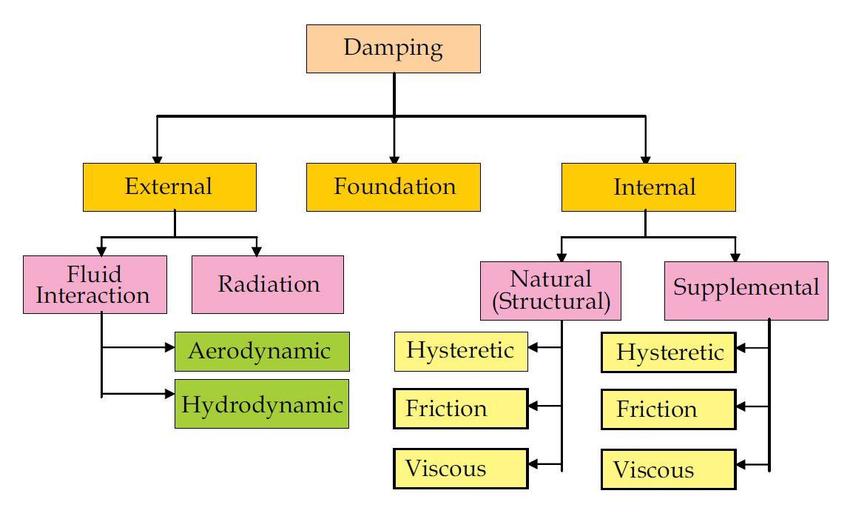
Damping is a phenomenon in which energy is dissipated in a system, typically reducing the amplitude of oscillations or vibrations over time. The sources of damping can vary depending on the system and the context, but the main sources generally include:
Sources of damping [Ref]
2.1. External Damping
- Fluid Interaction: This involves interaction with surrounding fluids (air, water, etc.).
- Aerodynamic Damping: Caused by the interaction between the structure and air.
- Hydrodynamic Damping: Caused by the interaction between the structure and water or other fluids.
- Radiation Damping: Energy loss due to the radiation of waves (such as sound or electromagnetic waves) from the structure.
2.2. Foundation Damping
This involves the interaction between the structure and its foundation, where energy is dissipated through various mechanisms such as:
- Hysteretic Damping: Energy loss due to internal friction within materials as they undergo cyclic deformation.
- Friction Damping: Energy loss due to friction between contacting surfaces.
- Viscous Damping: Energy loss due to the relative motion of a structure through a viscous medium (like a liquid). This could happen at boundaries or interfaces.
2.3. Internal Damping
Natural (Structural) Damping: Inherent damping mechanisms within the structure itself.
- Hysteretic Damping: Similar to the foundation category, this refers to energy loss due to the internal friction in the materials. All materials exhibit some degree of internal friction when subjected to stress, leading to energy dissipation. This is often represented by loss factors, which vary by material type. For example, rubber has a high loss factor (0.05–2), while metals like aluminum have a much lower range (0.0001–0.02).
- Friction Damping: Again, this involves energy loss due to friction between internal parts of the structure.
- Viscous Damping: Internal energy dissipation within materials, often modeled as a viscous effect.
2.4. Supplemental Damping
Added damping mechanisms to enhance the natural damping.
- Hysteretic Damping
- Friction Damping
- Viscous Damping
2.5. Friction, Viscous, and Coulomb damping
I’m sure you have already noticed that two types of damping exist in all categories: Friction and Viscous, right? It maybe seems a little confusing but here is break down:
We categorized the damping origins, where they come from which are Internal, External, and Foundation; but in each one the reason for them could be several things such as Friction and Viscous.
Now let’s make a definition of these two types and the one common one Coulomb (Dry) damping:
- Friction Damping can occur at the interfaces of joined structures (e.g., bolts or rivets) where sliding friction dissipates energy. The effectiveness of this damping can depend on how tightly the joints are secured.
- Viscous damping is common in systems where fluid motion occurs, viscous damping involves energy loss due to the resistance of a fluid (like oil) moving through a small opening, converting kinetic energy into heat.
- Coulomb damping arises from frictional forces between surfaces in contact, converting kinetic energy into heat through the sliding motion.
3. Why do we use Abaqus Damping?
Abaqus damping is used to model the dissipation of energy in a system during dynamic analysis. In real-world materials and structures, energy is lost due to various mechanisms like internal friction, material hysteresis, and interaction with the environment. These effects are collectively referred to as damping.
Here are the key reasons why damping is used in Abaqus simulations:
- Energy Dissipation: Damping allows the simulation to capture the energy loss that occurs in materials and structures when they are subjected to dynamic loads, such as vibrations, impacts, or cyclic loading. This energy loss is crucial for accurately predicting the behavior of the structure under dynamic conditions.
- Stability of Simulations: Including damping in a model helps in stabilizing the numerical solution, especially in transient dynamic analyses. Without sufficient damping, the simulation could exhibit non-physical oscillations or numerical instabilities.
- Realistic Response: Damping is essential for producing realistic simulation results, especially for systems where vibrational or dynamic behavior is critical. It ensures that the amplitude of oscillations decreases over time, reflecting the physical reality where systems naturally tend to settle into a steady state.
- Modeling Material Behavior: In some cases, damping is used to model specific material behaviors, such as viscoelasticity, where the material exhibits both elastic and viscous characteristics. In these cases, damping is part of the material’s constitutive model.
- Resonance Control: Damping helps to control resonance effects in structures. When a structure is excited at its natural frequency, damping reduces the amplitude of the resulting vibrations, preventing potential damage or failure due to excessive resonant oscillations.
4. How can we Model Damping in Abaqus?
| The most widely used damping form called viscous damping, in which the damping force is velocity proportional. In fact, the complex damping may be proportional to the square of velocity, such as the damping force of solid motion in liquid, and sometimes, it even has nothing to do with speed, such as the friction at the supports. |
Two primary aspects for defining Abaqus damping are available:
* Velocity-proportional
Viscous damping
** Displacement-proportional
Abaqus Structural damping (imaginary stiffness) is used in frequency domain dynamics and in mode-based transient dynamics.
5. How can we enter data for damping in Abaqus?
In Abaqus, damping can be defined and applied in various ways, each serving different purposes depending on the type of analysis and the nature of the model. The main categories of damping in Abaqus include:
5.1. Material Damping Abaqus
Material damping in Abaqus refers to the inherent energy dissipation within a material during deformation. This is crucial for accurately simulating real-world conditions where energy is lost due to material properties. In Abaqus, material damping is typically specified using Rayleigh damping, which combines mass proportional and stiffness proportional damping.
- Mass Proportional Damping: This type of damping is proportional to the mass matrix and simulates the effect of the material moving through a viscous medium. It primarily affects lower frequencies and is defined by the damping factor α. This is specified using the DAMPING option with ALPHA in the input file or through the MechanicalDamping: Alpha in ABAQUS/CAE.
- Stiffness Proportional Damping: This damping is proportional to the stiffness matrix and reflects the material’s internal dissipation mechanisms. It influences higher frequencies and is defined by the damping factor β. This is specified using the DAMPING option with BETA in the input file or through the MechanicalDamping: Beta in ABAQUS/CAE.
In ABAQUS/Standard, damping is applied directly as part of the material definition for linear and nonlinear materials, with the effects calculated based on the current state of the material during the analysis.
5.2. Element Damping
Element damping in Abaqus can be introduced through specific element types or through additional definitions in the model. This category includes:
- Dashpot Elements: These elements provide a damping force proportional to velocity and are useful for simulating viscous effects in the model.
- Spring Elements: While primarily used for stiffness, spring elements can be combined with dashpot elements to represent damping effects.
- Connector Elements: In connector elements, damping is introduced through connector damping properties, which can be specified for various types of connections.
Element damping is often used when material damping alone is insufficient to capture the damping characteristics of the structure, especially in cases involving complex interactions or additional dissipative components.
5.3. Abaqus Modal Damping
Modal damping is specific to mode-based linear dynamic analyses and is applicable only in ABAQUS/Standard. It involves defining damping for each mode or over specific frequency ranges:
- Rayleigh Damping: In modal damping, Rayleigh damping can be applied by specifying damping factors for individual modes or for frequency ranges. This type of damping combines both mass and stiffness proportional components and is defined using the MODAL DAMPING option with RAYLEIGH in the input file or through ABAQUS/CAE’s Step module.
- Composite Modal Damping: This involves defining damping factors for different materials and combining them into a single damping factor for each mode. It is calculated as a weighted average of the mass matrices associated with each material and can be specified for mode numbers using the DAMPING, COMPOSITE option.
Modal damping is useful for analyses where the dynamic response is dominated by specific modes and provides a way to incorporate damping effects directly related to those modes.
5.4. Artificial Damping
Artificial damping is associated with the numerical integration methods used in dynamic analysis. It is not a physical property but rather a computational tool to improve the stability of the numerical solution:
- Implicit Dynamics (ABAQUS/Standard): Artificial damping is introduced to enhance numerical stability, especially when using implicit time integration methods. It is controlled by the numerical damping control parameter and helps to manage high-frequency oscillations that can arise from numerical approximations.
- Explicit Dynamics (ABAQUS/Explicit): In explicit dynamic analysis, a small amount of numerical damping is automatically introduced to control high-frequency oscillations through bulk viscosity. This helps stabilize the solution but is typically minimal compared to physical damping effects.
Artificial damping is crucial for ensuring Abaqus convergence and stability in dynamic simulations but should be used carefully to avoid overly influencing the physical response of the model.
6. Material Damping Abaqus
In most cases, the material model itself may provide damping in the form of plastic dissipation or viscoelasticity. For many applications such damping may be adequate. Another option is to use Rayleigh damping or structural damping.
Material damping Abaqus can be defined for both direct-integration (nonlinear, implicit or explicit) and mode-based (linear) dynamic analyses.
Here are the main points for using material damping in Abaqus:
-
Simulate Realistic Dynamics: Real-world structures exhibit energy loss due to internal friction and other factors. Material damping allows you to capture this phenomenon in your Abaqus model, leading to more accurate simulations of dynamic behavior like vibrations or impacts.
-
Control Unwanted Oscillations: Damping helps prevent numerical oscillations that can sometimes arise in simulations, especially when dealing with very fast phenomena or noisy dynamics. This improves the stability and convergence of your Abaqus analysis.
-
Focus on Key Responses: By introducing damping, you can expedite the decay of transient vibrations in your model. This allows you to focus on the long-term response or steady-state behavior of the structure, potentially saving computational time.
-
Tailor Damping to Materials: Abaqus offers various material damping models, such as Rayleigh Damping, that let you specify damping properties relevant to the materials in your model. This enhances the realism of your simulations.
Overall, material damping in Abaqus is a crucial tool for accurately representing energy dissipation and achieving meaningful results in dynamic analysis.
Many civil engineering problems share similarities with mechanical problems. However, there are numerous challenges that are unique to civil engineering and require a specialized approach. To address this, we’ve developed a tailor-made version of the Abaqus for Beginners tutorial specifically for civil engineers. You can claim your copy of this specialized tutorial by clicking the package below.
7. Forms of Material Damping in Abaqus
♦ Rayleigh damping (Viscous damping)
♦ Structural damping
♦ Viscoelasticity (for viscoelastic materials)
In the following sections, we’re going to fully discuss the forms of material damping. Now, let’s start with Abaqus Rayleigh damping.
Read more: What is Abaqus Contact Damping and how to apply it in Abaqus?
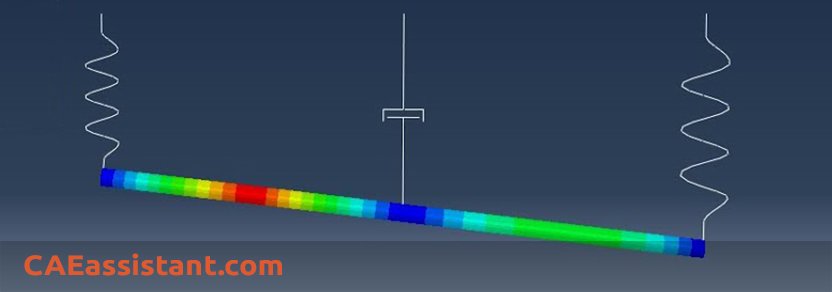
7.1. Rayleigh Damping Abaqus
Some models do not have any dissipation sources (an example is a linear system with chattering contact, such as a pipeline in a seismic event). In such cases, it is often desirable to introduce some general damping. Abaqus provides Rayleigh damping for this purpose. It provides a convenient abstraction to damp lower (mass-dependent) and higher (stiffness-dependent) frequency range behavior. (material damping)
In the Rayleigh model, damping is linearly proportional to mass M and stiffness K matrices. A damping matrix C is added to the system. We define C as:
C matrices are generated for each material in the model. We define the Rayleigh damping factors (alpha, beta) as material properties in Abaqus:
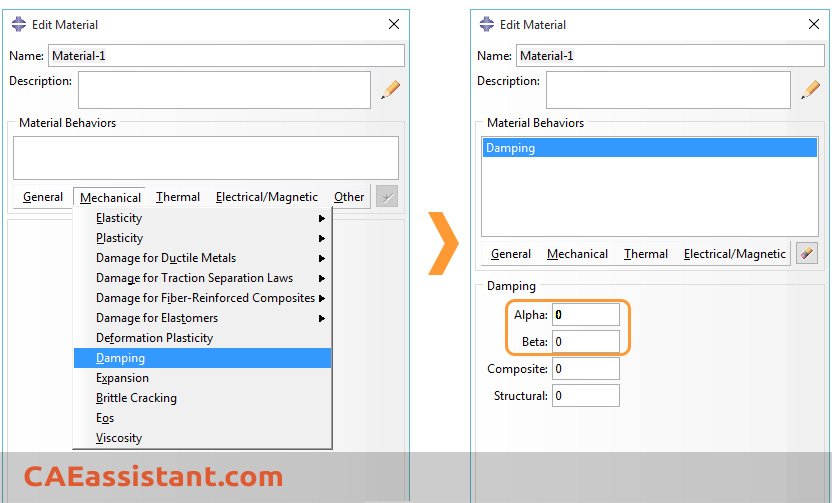
To define Abaqus Rayleigh damping, we need to calculate alpha and beta. For this purpose, let’s assume our objective is to impose a 5% damping ratio on a structure. To accomplish this, we will perform a modal analysis to determine the frequencies, denoted as omega 1 and omega 2, associated with the first and second modes. Then, using these frequencies, we will calculate the alpha and beta values.
Reminder. Damping Ratio………………………………………………………………………………………………..
The fraction of critical damping or damping ratio is defined as:
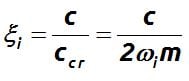
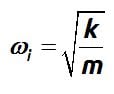
………………………………………………………………………………………………………………………………………………………………………..
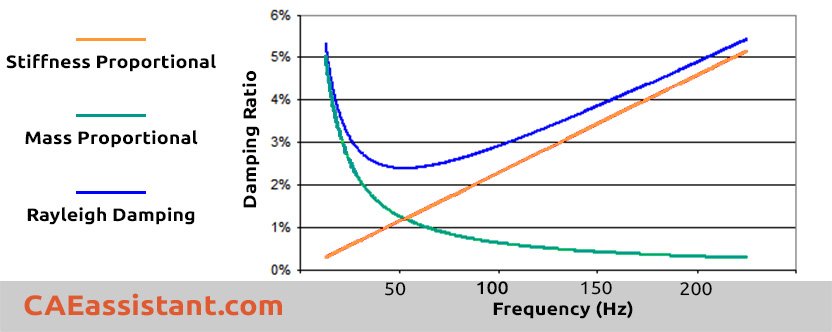
Thus, mass-proportional damping dominates when the frequency is low, and stiffness-proportional damping dominates when the frequency is high:
The orange line shows stiffness-proportional damping, which is straightforward because the damping ratio goes up as frequency goes up. On the other hand, the green line represents mass-proportional damping, where the damping ratio decreases as frequency increases, making a wavy curve. Often, you’ll see both of these damping types together, and their combined effect is shown by the blue line. Here’s the fascinating part: when the natural frequency is low, mass-proportional damping is more important, but for higher natural frequencies, stiffness-proportional damping becomes more significant.
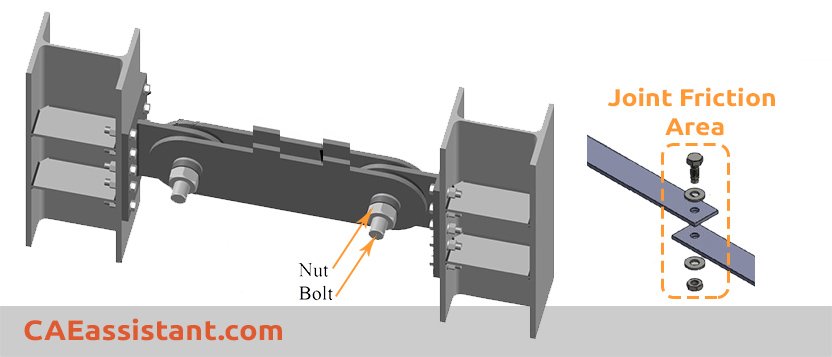
7.2. Abaqus Structural Damping
Assumes that the damping forces are proportional to the forces caused by stressing of the structure and are opposed to the velocity:
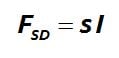
The damping forces due to structural damping are intended to represent frictional effects (as distinct from viscous effects). Thus, structural damping is suggested for models involving materials that exhibit frictional behavior (hysteretic damping) or where local frictional effects are present throughout the model, such as dry rubbing of joints in a multi-link structure.
7.3. Viscoelasticity
Let me provide a brief explanation of what viscoelastic materials are and how we can utilize them in Abaqus.
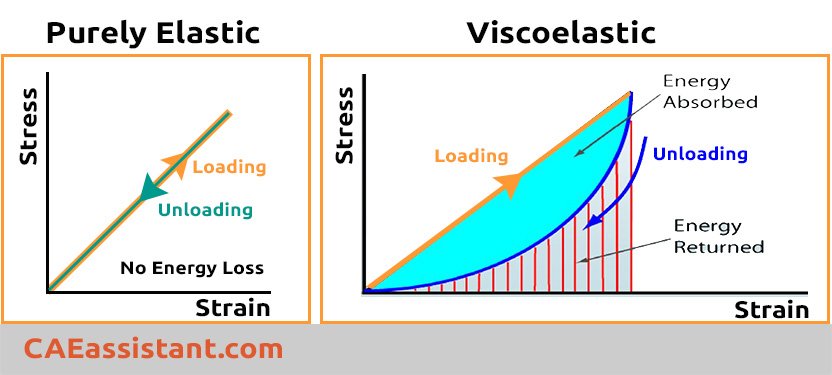
In the world of materials, elastic substances follow Hooke’s law, where stress is directly linked to strain.
This means that when we apply a load to an elastic material, there will be an instantaneous deformation. As long as we maintain the applied load, the deformation will remain constant. When we remove the load, all of the deformation will be fully recovered, demonstrating that elastic materials return to their original shape once the load is removed. On the other hand, viscous materials follow a different behavior, obeying the following law:
Where stress is directly proportional to strain rate not strain. Viscoelasticity is the property of materials that exhibit both viscous and elastic characteristics when undergoing deformation. The term viscous implies that they deform slowly when exposed to an external force. They cannot return to their first configuration. It is due to dissipation of energy. Elastic materials strain when stretched and immediately return to their original state once the stress is removed. Viscoelastic materials have elements of both of these properties:
Viscoelastic Abaqus model is useful for materials in which dissipative losses primarily caused by viscous (internal damping) effects. The model must be combined with an elastic material model. Viscoelasticity cannot be combined with any of the plasticity models. To delve deeper into this subject, check out the next section “Abaqus viscoelastic tutorial”, which will guide you through the modeling and simulation process using Abaqus software.
Read More: The meaning of specific internal energy and dissipated inelastic specific energy
 |
⭐⭐⭐Free Abaqus Course | ⏰10 hours Video 👩🎓+1000 Students ♾️ Lifetime Access
✅ Module by Module Training ✅ Standard/Explicit Analyses Tutorial ✅ Subroutines (UMAT) Training … ✅ Python Scripting Lesson & Examples |
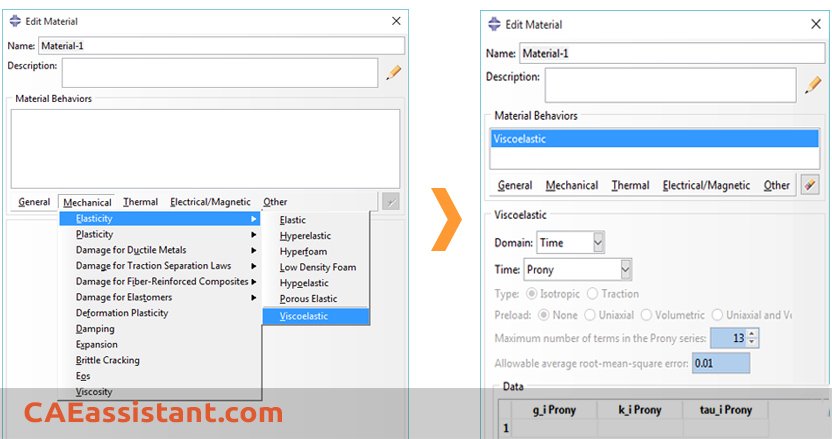
7.3.1. Defining viscoelasticity in Abaqus(Viscoelastic Abaqus)
Viscoelastic Abaqus can be defined as:
* Time-domain viscoelasticity
Viscoelasticity is a function of time for transient analysis. It describes isotropic rate-dependent material behavior. We can use a Prony series formulation to enter data:
The Prony series Abaqus is an equation that describes the relationship between shear modulus (G) and time (T).
In this equation, T represents time, G(t) denotes the shear modulus at a given time, Gi represents the relaxation modulus, and τ represents the relaxation time. To fully characterize the parameters in the Prony series, we need to start by defining the instantaneous shear modulus. Additionally, we must define the relaxation modulus and relaxation time. Depending on the chosen value of ‘N’, we have to use a table that lists various values of relaxation modulus and relaxation time.
Furthermore, it’s important to define the instantaneous Young’s modulus, instantaneous Poisson’s ratio, and density to comprehensively describe the material’s behavior.
So, this was all about viscoelastic Abaqus using the Prony series. Let’s now explore Frequency domain viscoelasticity.
** Frequency domain viscoelasticity
Viscoelasticity in Abaqus is a function of frequency for steady-state small-vibration analyses. This analysis is limited to Abaqus/Standard.
For example, many applications of elastomers involve dynamic loading in the form of steady-state vibration, and often in such cases, the dissipative losses in the material must be modeled to obtain useful results.
Here are the main points about defining viscoelastic materials in Abaqus:
-
Capture Time-Dependent Behavior: Viscoelastic materials exhibit properties that change with time. Defining them in Abaqus allows you to simulate real-world materials like polymers, rubber, or some biomaterials that exhibit both elastic (recoverable) and viscous (irreversible) deformation under stress.
-
Advanced Material Modeling: Abaqus offers various viscoelastic material models, including Prony series, Prony series with relaxation spectrum, and others. These models capture the complex stress-strain response of viscoelastic materials over time.
-
Simulate Creep and Stress Relaxation: Creep refers to the increasing deformation under constant stress, and stress relaxation describes the decrease in stress over time under constant strain. Defining viscoelastic materials allows you to analyze these phenomena crucial for understanding long-term behavior of structures.
-
Frequency-Dependent Analysis: Viscoelastic properties can vary with loading frequency. Abaqus allows you to define viscoelasticity in the time domain or frequency domain, enabling analysis of structures under dynamic or cyclic loading.
-
Increased Simulation Accuracy: By incorporating viscoelastic behavior, you can achieve more realistic simulations of structures made from these materials. This is crucial for applications like vibration analysis, fatigue analysis, or understanding the long-term performance of components.
Eager to hear from you…
The CAE Assistant is committed to addressing all your CAE needs, and your feedback greatly assists us in achieving this goal. If you have any questions or encounter complications, please feel free to comment here.
You can have the PDF of this page by clicking on In Detail: Abaqus Damping
| ✅ Subscribed students | +80,000 |
| ✅ Upcoming courses | +300 |
| ✅ Tutorial hours | +300 |
| ✅ Tutorial packages | +100 |
What is damping?
Damping is an influence within or upon a dynamic system that has the effect of reducing, restricting or preventing its movements. In physical systems, damping is produced by processes that dissipate energy.
What are the Sources of Damping?
Generally, Damping results from several sources, such as inelastic dissipation (Material nonlinearity), material behavior (Internal friction), and joint behavior (External friction).
How can we model damping in Abaqus?
There are two primary aspects for defining damping available in Abaqus. The most widely used damping form is called viscous damping, in which the damping force is velocity-proportional. Sometimes the damping force is Displacement-proportional such as the friction at the supports. This damping form is called Structural damping (imaginary stiffness).
What is the benefit of using damping in physical systems?
There are two main reasons for adding damping to a model: to limit numerical oscillations or to add physical damping to the system. Damping is also beneficial when modeling high-speed phenomena and noisy dynamics.
What is the damping definition sources in Abaqus?
In general, Abaqus has five categories of damping definition sources: Abaqus Material damping, Element damping (spring elements, dashpot elements, and connector elements), Abaqus global damping (constant damping coefficient), Modal damping (in mode-based linear dynamic analyses), and Artificial damping (numerical damping).
What are the forms of Material Damping in Abaqus?
There are three options to provide material damping in Abaqus. The viscoelasticity model is useful for materials in which dissipative losses are primarily caused by viscous (internal damping) effects. Rayleigh damping Abaqus (Viscous damping) is used to introduce general damping in models without dissipation sources (an example is a linear system with chattering contact, such as a pipeline in a seismic event). Another option is to use Abaqus structural damping. The damping forces due to structural damping are intended to represent frictional effects (as distinct from viscous effects).



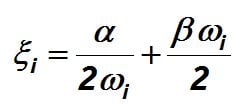
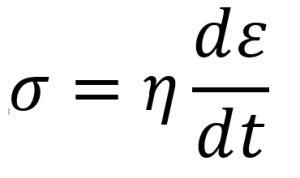

Really thank you! Want more.
Very interesting information!Perfect just what I was searching for! Filia Kendrick Teriann