In Abaqus, specific internal energy and dissipated inelastic specific energy are key concepts that help capture the energy dynamics in a material. Specific internal energy refers to the internal energy per unit mass, while dissipated energy is the energy converted into other forms and lost from the system. These concepts are essential for analyzing thermodynamic behavior, energy losses, and material deformation.
This blog explores these critical aspects in detail. We will cover the definitions and importance of specific internal energy and dissipated energy, delve into the concept of inelastic energy, and explain the energy balance in Abaqus. Finally, we’ll discuss the significance of these energies in VUMAT and the importance of updating them in simulations.
1. Specific Internal Energy and Dissipated Inelastic Specific Energy | Abaqus Internal Energy
In Abaqus “specific internal energy” refers to the internal energy per unit mass of a material. It is a thermodynamic property that describes the energy stored within a material due to its microscopic structure and interactions between its constituent particles. The specific internal energy is a key parameter in Abaqus simulations that helps capture the thermodynamic behavior and energy distribution within a material or system.
The internal energy (IE/Abaqus Internal Energy) is the sum of the recoverable elastic strain energy, EE; the dissipated inelastic energy (dissipated through inelastic processes such as plasticity), PE; the energy dissipated through viscoelasticity or creep, CDE; and the artificial strain energy (includes energy stored in hourglass resistances and transverse shear in shell and beam elements), AE:
IE = EE + PE + CDE + AE
Specific here means per unit of mass.
Click on the link below to see all the model energy output variables in Abaqus:
2. What is dissipated energy? | Dissipated Energy Abaqus
In Abaqus, “dissipated energy” refers to the energy that is converted into other forms, typically in the form of heat or work, and is lost from the system during a simulation. It represents the energy that is not recoverable or stored within the system but is instead dissipated as a result of various phenomena such as material deformation, friction, or viscous effects (Dissipated Energy Abaqus).
Dissipated energy can arise from different sources depending on the nature of the analysis. For example, in a mechanical analysis, it can be associated with plastic deformation, material yielding, and the associated hysteresis effects. In a thermal analysis, it can be related to heat conduction, convection, and radiation losses.
Abaqus provides several methods to evaluate and quantify the dissipated energy during a simulation. These methods depend on the specific analysis being performed. For instance, in a structural analysis, the dissipated energy can be computed from the stress-strain relationship using the plasticity or damage models incorporated in the material properties. Abaqus provides output variables and history outputs that can be used to extract and track the dissipated energy during the simulation.
Understanding and monitoring the dissipated energy in Abaqus can provide valuable insights into the behavior and response of a system, such as identifying regions of high energy losses, assessing the efficiency of a design, or evaluating the fatigue life of a structure.
3. What is inelastic energy?
In Abaqus, “inelastic energy” refers to the portion of the total energy within a system that is associated with irreversible deformations or material behavior. It represents the energy that is dissipated or lost due to inelastic processes, such as plastic deformation, material yielding, or damage accumulation.
When a material undergoes inelastic behavior, such as plasticity or viscoelasticity, some of the energy input into the system is converted into heat or dissipated in other forms. This dissipated energy is considered as inelastic energy. It is not recoverable and does not contribute to the elastic or stored energy within the system.
Abaqus provides the capability to compute and evaluate the inelastic energy during simulations. The inelastic energy can be calculated based on the constitutive models and material properties used in the analysis. Abaqus offers various material models, such as plasticity models, damage models, and viscoelastic models, which enable the estimation of inelastic energy.
By analyzing the inelastic energy distribution and evolution, engineers and researchers can gain insights into the behavior of materials and structures under different loading conditions. It helps in assessing the extent of irreversible deformations, predicting failure or fatigue, and optimizing designs to minimize energy losses.
See Also:
Training Package: Introduction to UMAT and VUMAT Subroutines
4. Energy balance in Abaqus
In Abaqus, an energy balance is a fundamental concept used to track the flow of energy within a system during a simulation. It involves accounting for different forms of energy, such as kinetic energy, potential energy, and internal energy, and their interconversion within the system.
The energy balance equation in Abaqus is derived from the principle of conservation of energy, stating that the total energy within a closed system remains constant unless energy is added to or removed from the system. The energy generated is frequently a crucial aspect of ABAQUS/Explicit analysis. Assessing and comparing different energy elements can aid in determining if the analysis is producing a suitable outcome.
We can express the overall energy balance of the model as follows:
The sum of the internal energy , viscous energy dissipation , frictional energy dissipation , kinetic energy , and work done by externally applied loads equals a constant value denoted as . In the numerical model, the value of remains approximately constant, typically with an error of less than 1%.
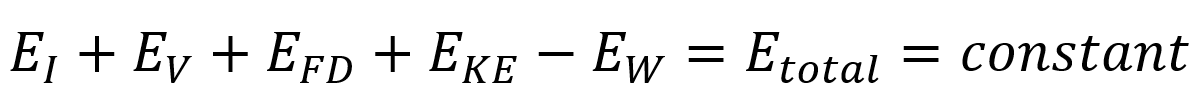
5. The meaning of specific internal energy and dissipated inelastic specific energy in VUMAT
What is the meaning of specific internal energy and dissipated inelastic specific energy in VUMAT? Can I ignore calculating specific internal energy and dissipated inelastic specific energy in VUMAT?
Currently, I’m coding a damaged plasticity model in VUMAT, and it works well for 1 element without calculating specific internal energy and dissipated inelastic specific energy. However, for many elements, the results are not reasonable, so this means the specific internal energy and dissipated inelastic specific energy affect my results?
Thanks so much for your time!
5.1. Updating Internal and Dissipated Inelastic Energies in VUMAT
When writing a VUMAT, the following quantities must be defined:
» Stress at the end of an increment
» SDVs (if there is any) at the end of an increment
But internal and dissipated energies at the end of the increment may be defined.
If you have any problem with the VUMAT results (stresses, strains, etc.) it can not be due to updating energies. You should investigate stress updating terms.
Now, let me ask you a question. What about the UMAT subroutine? I mean, do you think we should check the stresses for this same issue in the UMAT subroutine? What are the differences between the UMAT and VUMAT subroutines, especially in the stress terms calculations? If you check out the “Writing UMAT subroutine” section in the Abaqus tutorial, you will have your answers. Trust me, it’ll make it worth your while.
6. Conclusion
This blog delves into the concepts of specific internal energy and dissipated inelastic energy within Abaqus, critical parameters for understanding material behavior and energy distribution in simulations. The importance of these concepts lies in their role in capturing thermodynamic behavior and assessing energy losses, which are crucial for accurate simulation results and design optimization.
The blog is structured into several sections. The first section defines specific internal energy, describing it as the internal energy per unit mass, encompassing elastic strain energy, dissipated inelastic energy, viscoelastic or creep energy, and artificial strain energy. The second section explains dissipated energy, highlighting its conversion into heat or work during deformation or friction. The third section covers inelastic energy, detailing its association with irreversible deformations and material behavior. The fourth section discusses the energy balance in Abaqus, emphasizing the conservation of energy within a system during simulation. The final section addresses the meaning and calculation of specific internal energy and dissipated inelastic energy in VUMAT, particularly in the context of coding a damaged plasticity model.
In conclusion, this article provides a comprehensive overview of the critical energy parameters in Abaqus, emphasizing their importance in accurately capturing material behavior and ensuring reliable simulation results. Understanding these concepts aids in optimizing designs and assessing the efficiency and fatigue life of structures.
Users ask these questions
Now, let’s see the common questions users ask about energy in Abaqus. We answered them and offered the proper content (blog or product) for it.
I. Dynamic Explicit and fluctuation in kinetic energy
Q: Hi everybody,
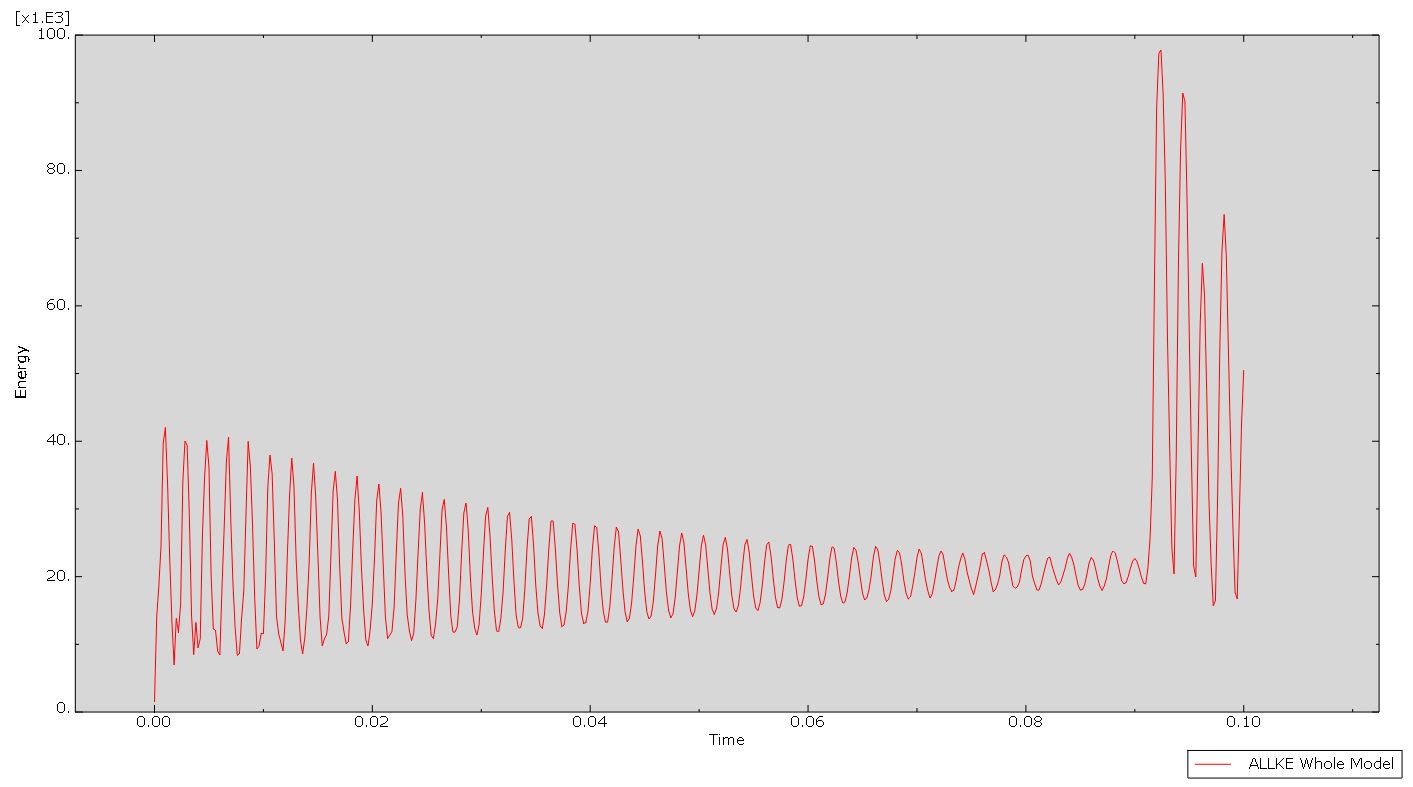
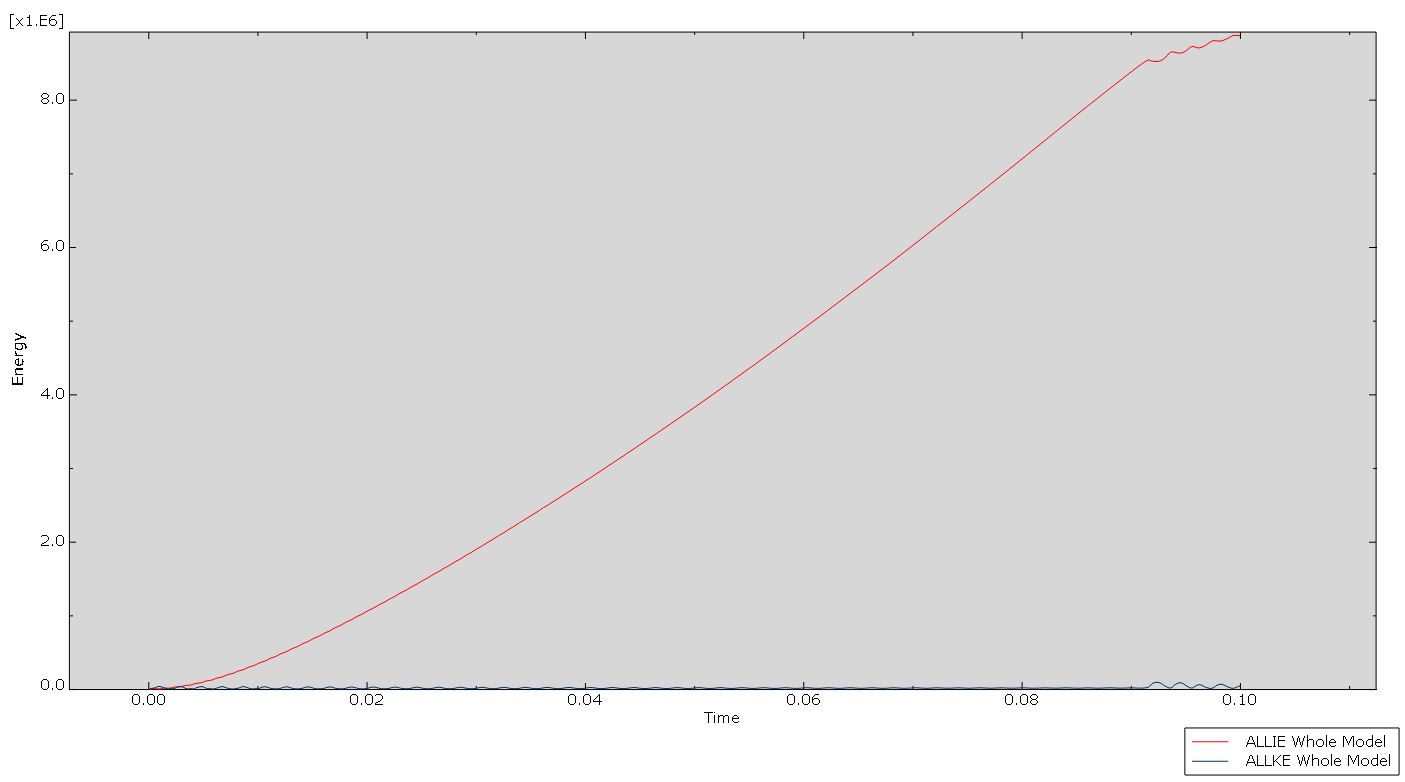
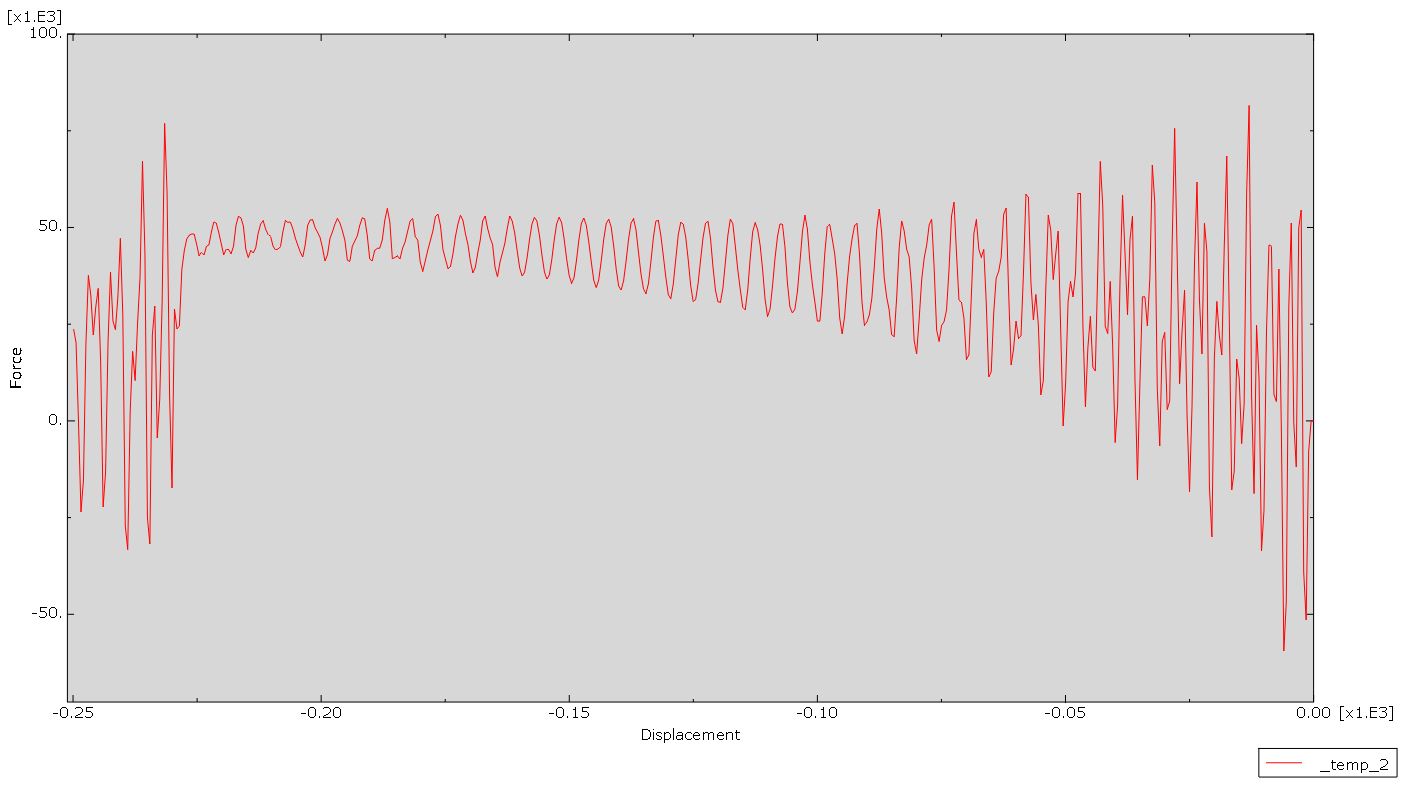
I am getting something weird from my ABAQUS dynamic explicit analysis output, i.e. my kinetic energy curve is fluctuating (ALLKE), as shown in the image below. I’ve already verified that the kinetic energy (ALLKE) is significantly lower than the internal energy (ALLIE), but I’m still receiving a very noisy force-displacement curve, which I believe is due to my fluctuating ALLKE. Is anyone else ever in a situation like this?
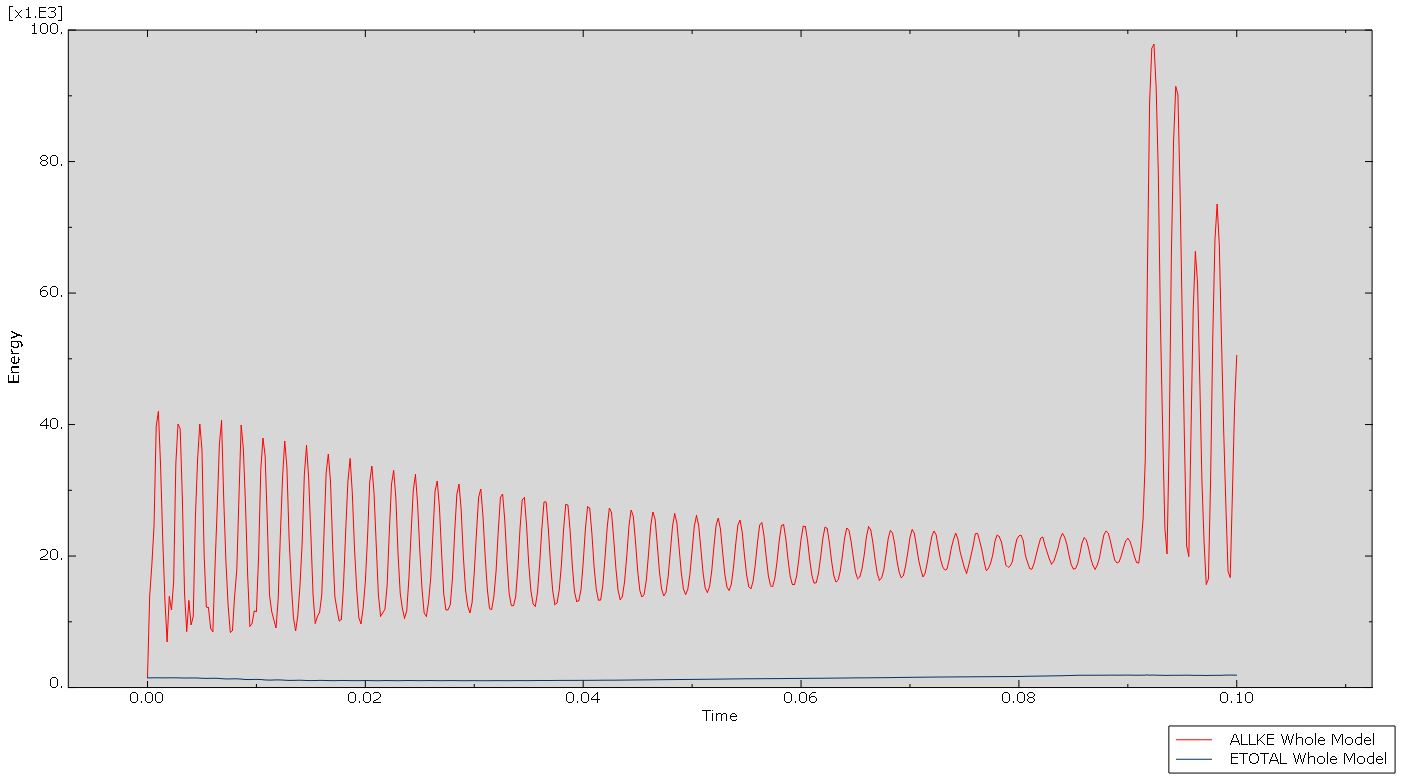
Is it common to have ALLKE higher than ETOTAL, as seen in the image below?
Thank you so much for any suggestions!
A: First of all, it is common to have some noises in the ABAQUS/Explicit as shown in your ALLKE plot. However, you have noises with large amplitude at the end of your ALLKE plot. You should check out what has happened to your model at this time. Moreover, the ETOTAL is the sum of several different energies. In other words, it is a sum of several minus and positive values. So, it may or not ALLKE is greater than the ETOTAL.
I recommend you check the following links to learn more: