What is Abaqus Small Sliding? | Finite Sliding VS Small Sliding

1. What is Abaqus small sliding and Finite Sliding?

In Abaqus, “small sliding” and “finite sliding” refer to different modeling assumptions for contact behavior.

Small sliding assumes that the contact surfaces remain nearly parallel and that relative sliding between them is minimal. It implies that the tangential displacements between the contacting surfaces are small compared to the contact dimensions. In this case, the frictional forces at the contact interface are typically ignored or approximated using simplified models. Small sliding is suitable when the relative sliding between the surfaces is expected to be negligible.

Finite sliding considers significant relative sliding between the contact surfaces. It allows for large tangential displacements and rotations at the contact interface. Frictional forces and moments are taken into account, and the contact behavior is more accurately modeled. Finite sliding is appropriate when the relative sliding between the surfaces is expected to be significant and cannot be neglected.

The choice between small sliding and finite sliding depends on the specific problem and the expected relative sliding behavior between the contact surfaces.

1.1. Example of small sliding

Here’s an example where small sliding would be more appropriate than finite sliding:

Consider a simple bolted joint where two parts are connected by bolts. The contact surfaces between the parts and the bolt heads/nuts are in contact. In this scenario, the primary purpose of the bolts is to provide clamping force and maintain the integrity of the joint, rather than transmitting significant relative motion between the parts.

In such a case, the relative sliding between the contact surfaces is expected to be minimal or negligible during normal operation. The contact surfaces remain relatively parallel, and the primary concern is the distribution of clamping forces and stress concentrations.

In this situation, using small sliding assumptions would be more appropriate. The small sliding assumption simplifies the modeling process by neglecting or approximating the frictional forces at the contact interface. It can significantly reduce computational cost and provide reasonable accuracy for the problem at hand, as long as the relative sliding between the contact surfaces remains small.

By assuming small sliding, you can focus on the overall clamping behavior and stress distribution, while simplifying the contact modeling aspect.

3.2. Example of finite sliding

Here’s an example where finite sliding would be more appropriate than small sliding:

Consider a mechanical system with two components that are in contact, such as a gear mechanism. In this case, the relative motion between the contacting surfaces is significant, and sliding occurs as the gears rotate and engage with each other. The relative sliding between the gear teeth is essential for the proper functioning of the system.

In this scenario, utilizing small sliding assumptions would not accurately capture the behavior of the system. The assumption of small sliding neglects the significant relative motion and rotation between the gear teeth, which is essential for analyzing the actual contact forces and moments.

Using finite sliding assumptions becomes more appropriate in such cases. Finite sliding allows for large tangential displacements and rotations at the contact interface, accommodating the relative motion between the surfaces accurately. Frictional forces and moments are considered, enabling a more realistic representation of the contact behavior and the resulting forces and stresses in the system.

By employing finite sliding assumptions, you can accurately capture the dynamic behavior of the gear mechanism, analyze the effects of relative motion, and assess factors such as contact stresses, wear, and energy losses associated with sliding between the contacting surfaces.

2. Finite sliding VS small sliding 

Several factors should be considered when deciding between finite sliding and small sliding in Abaqus. These factors include:

Magnitude of relative sliding: Consider the expected magnitude of relative sliding between the contacting surfaces. If the sliding is anticipated to be significant, with large tangential displacements and rotations, finite sliding should be used to accurately capture the contact behavior. On the other hand, if the sliding is expected to be minimal or negligible, small sliding can be employed to simplify the analysis.

Importance of frictional effects: Assess the significance of frictional forces and moments at the contact interface. If friction plays a crucial role in the behavior of the system, such as in gear mechanisms or sliding joints, finite sliding should be used to accurately model these effects. Small sliding assumptions typically neglect or approximate frictional forces, which may not be suitable for systems where friction is important.

Computational efficiency: Consider the computational resources available and the desired analysis speed. Small sliding assumptions can significantly reduce computational costs compared to finite sliding. If computational efficiency is a priority and the relative sliding is minimal, small sliding can be a suitable choice to simplify the analysis while still providing reasonable results.

Accuracy requirements: Evaluate the required level of accuracy for the analysis. Finite sliding provides a more detailed and accurate representation of the contact behavior, accounting for large displacements, rotations, and frictional effects. If a high level of accuracy is necessary, particularly when studying wear, energy losses, or contact stresses, finite sliding should be employed. However, if the analysis can tolerate some simplification and sliding is limited, small sliding can be a reasonable choice with acceptable accuracy.

It is important to carefully assess these factors and choose the appropriate sliding assumption based on the specific problem, the expected behavior of the contact surfaces, and the desired level of accuracy and computational efficiency for the analysis. (finite sliding vs small sliding)

First, let’s make a definition for small and finite sliding:

Finite sliding means any arbitrary motion of the surfaces is allowed in contact.

Small sliding implies that when two bodies are in contact and may have large motion, a relatively small sliding will occur between two surfaces; Or both absolute and relative motion of the surfaces assumes to be small.

Note that the small sliding cannot be used in the Penalty contacts algorithm and self-contact.

We use small sliding when we are sure the motion between surfaces is small. Although using this formulation will solve the problem faster, use it carefully because it may cause errors and make an infinite master surface.

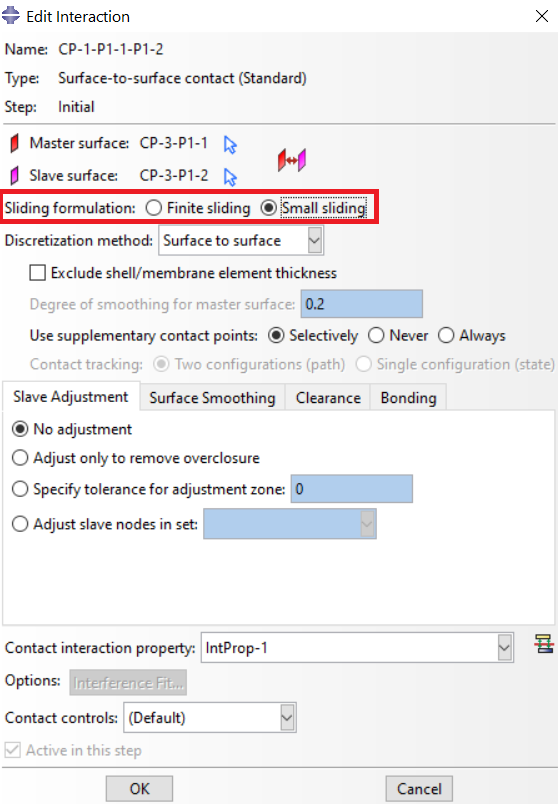
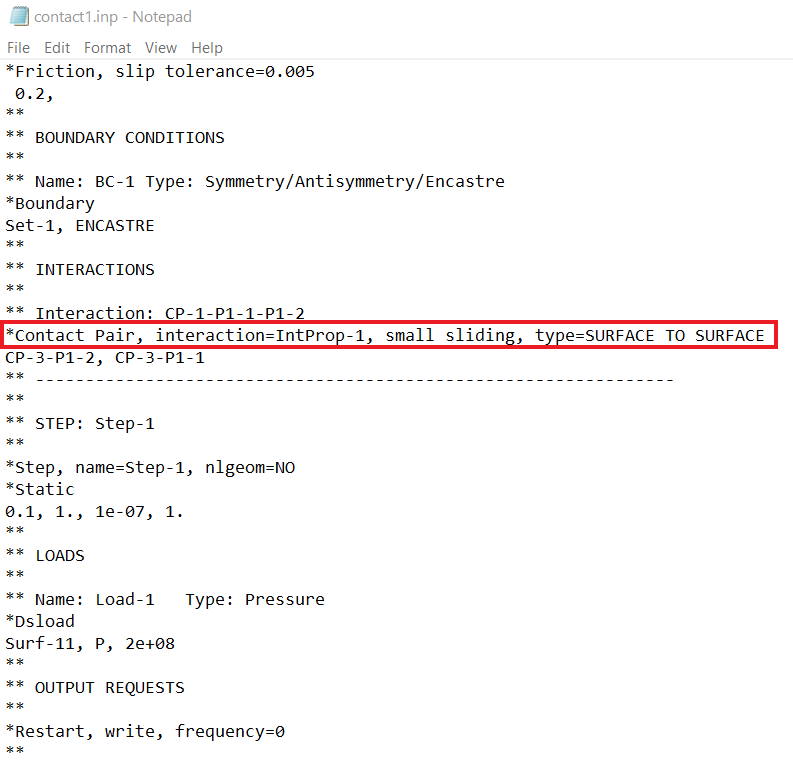
There are two ways to use the small sliding, through GUI or input file (see Figures 1 and 2).

Figure 1: select small sliding through GUI

Figure 2: small sliding through input file