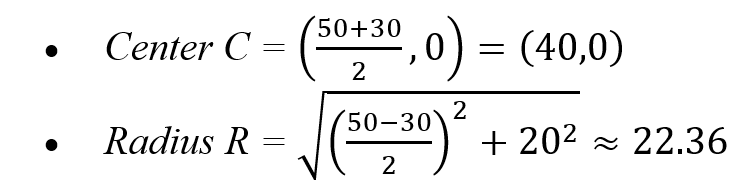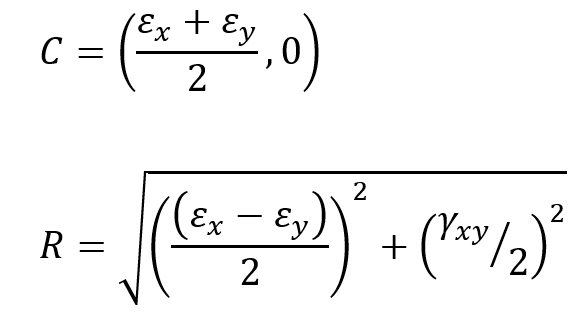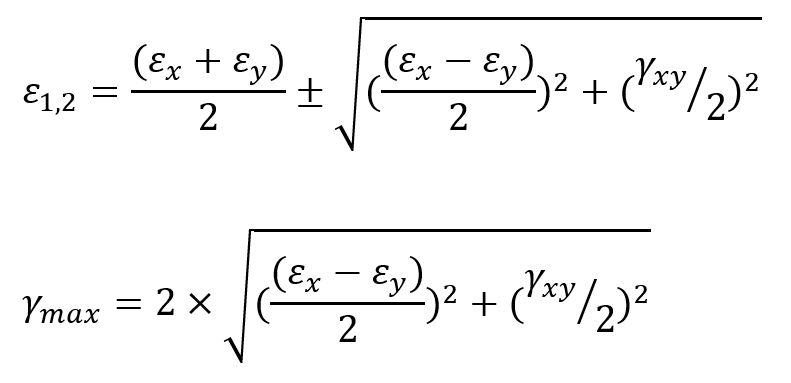What is Von Mises Stress? | Mohr’s Circle and Principal Stress and Strain

In the world of engineering, accurately predicting how materials will behave under stress is essential. One key concept in this domain is the Von Mises stress, a valuable tool used to forecast when a material might start to yield or fail under various loading conditions. This type of stress analysis is particularly significant when working with ductile materials, which need to withstand complex stress states without undergoing permanent deformation.
The Von Mises stress helps engineers simplify the complex stress states that occur in materials. It combines the effects of different stress components into a single value, making it easier to compare against a material’s yield strength. By using this criterion, engineers can better understand how and when a material might reach its breaking point, ensuring that designs are both safe and effective.
In this blog, we will explain Von Mises stress, a scalar value used to predict when materials yield under complex loading. We also compare this criterion with others like Tresca and Rankine, noting its accuracy for ductile materials. Moreover, we discuss principal stresses and strains, their calculation, and visualization using Mohr’s Circle. Finally, we highlight the role of Von Mises stress in finite element analysis (FEA) with Abaqus, crucial for ensuring structural safety and reliability.
1. What is Von Mises stress?
Von Mises stress, also known as the equivalent stress, is a scalar stress value derived from the stress state at a point and is used in engineering to predict the yielding of materials under any loading condition.
The Von Mises stress ( ) is calculated from the principal stresses (
) using the following formula:
Alternatively, in terms of the stress components in the x, y, and z directions ( ) and the shear stresses (
), the Von Mises stress is given by:
For a 2D stress state, it simplifies to:
Example: Consider a point in a material subjected to the following stress state:
Using the formula:
|
Explore our comprehensive Abaqus tutorial page, featuring free PDF guides and detailed videos for all skill levels. Discover both free and premium packages, along with essential information to master Abaqus efficiently. Start your journey with our Abaqus tutorial now! |
 |
In this Abaqus training package for beginners, which is designed for FEM Simulation students in mechanical engineering, various examples in the most widely used fields are presented:
|
2. What is Von Mises criterion?
The Von Mises criterion, also known as the Von Mises yield criterion or the maximum distortion energy criterion, is a formula used to predict the yielding of ductile materials under complex loading conditions. Although the von Mises stress is a scalar value, the von Mises criterion uses this stress to determine the failure of a material. It states that yielding begins when the second deviatoric stress invariant reaches a critical value, which corresponds to the yield stress of the material in uniaxial tension. It is particularly useful in the fields of material science and mechanical engineering.
2.1. Formula
The Von Mises criterion is expressed mathematically as:
Where is the yield strength of the material.
Example: consider a point in a material subjected to the following stress state and the yield stress is 250 MPa:
Using the formula:
Since 223.6 MPa < 250 MPa, the material will not yield under these conditions.
2.2. Graphical presentation
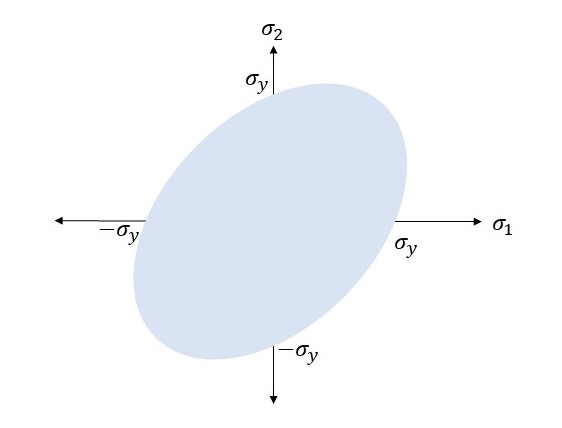
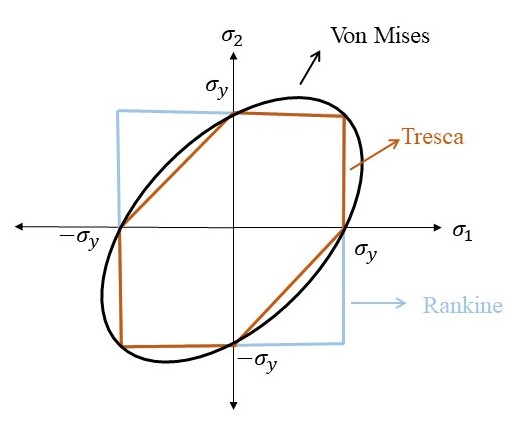
The Von Mises yield criterion can be represented in the principal stress space ( ) as an ellipse or ellipsoid. In the 2D principal stress plane
, it appears as an ellipse. This plot shows the combination of principal stresses that will cause yielding according to the Von Mises criterion if the von Mises stress exceeds its limits.
Figure 1: 2D Von Mises graphical presentation
2.3. Other Failure Criteria
- Tresca Criterion: The Tresca yield criterion (maximum shear stress criterion) is another commonly used criterion for ductile materials. It states that yielding occurs when the maximum shear stress reaches the shear yield stress of the material. The Tresca criterion is more conservative than the Von Mises criterion, predicting yielding at lower stress levels. Von Mises theory can more accurately predict failure. This can mean optimal use of materials
- Rankine criterion: This criterion, also known as the maximum normal stress criterion, is often used for brittle materials and considers both normal stresses. The maximum stress criterion states that failure occurs at a point in brittle material when a principal stress reaches either the uniaxial tensile or compressive strength. It is more suitable for materials like concrete and soils.
Figure 2: Von Mises, Tresca, and Rankine graphical presentation
2.4. Why should we use the Von Mises criterion?
Predicting Yielding: Von Mises stress is particularly useful for predicting the onset of yielding in ductile materials under complex loading conditions. It combines the effects of all three principal stresses into a single equivalent stress value that can be compared directly to the material’s yield strength.
Material Safety: By using Von Mises stress, engineers can ensure the safety and reliability of structures and mechanical components. This stress criterion helps in designing components that can withstand operational loads without undergoing permanent deformation.
Simplicity and Accuracy: The Von Mises criterion simplifies the assessment of complex stress states and provides accurate predictions of yielding for ductile materials. It is widely accepted and used in engineering design and analysis.
Design Standards: Many engineering design standards use the Von Mises stress criterion for evaluating material failure. It provides a common basis for comparing the performance and safety of different materials and designs.
 |
⭐⭐⭐Free Abaqus Course | ⏰10 hours Video 👩🎓+1000 Students ♾️ Lifetime Access
✅ Module by Module Training ✅ Standard/Explicit Analyses Tutorial ✅ Subroutines (UMAT) Training … ✅ Python Scripting Lesson & Examples |
3. What are principal stresses and strains?
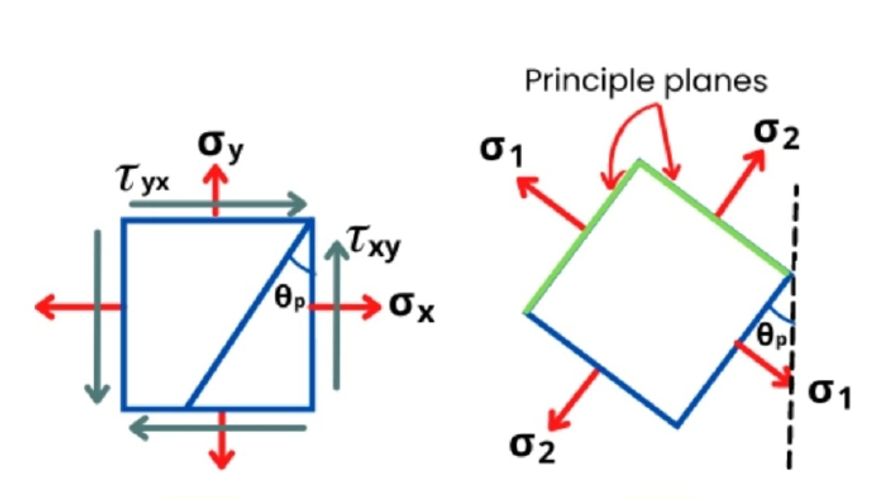
Principal Stresses: Principal stresses are the normal stresses that occur at particular orientations where the shear stress is zero. These stresses are the eigenvalues of the stress tensor and represent the maximum and minimum normal stresses that a material element experiences. They are crucial for understanding the state of stress at a point in a material.
Principal Strains: Principal strains are the normal strains that occur in the directions of the principal stresses. Similar to principal stresses, these strains represent the maximum and minimum normal strains that a material element experiences. They are the eigenvalues of the strain tensor.
Principal angle: This is the orientation angle at which the principal stresses or strains occur in a material. In other words, it’s the angle between the original coordinate system (usually aligned with the material’s axes) and the axes along which the principal stresses or strains are aligned. At this angle, the shear stress is zero, and the normal stresses reach their maximum or minimum values, known as the principal stresses.
Figure 3: Elements of material under subjected stress and principal stresses
3.1. Maximum and Minimum principal stresses
To find the principal stresses, we need to solve the characteristic equation derived from the stress tensor. The principal stresses and
which are respectively the maximum and minimum principal stresses are given by:
Example: consider a 2D stress state with the following components:
The principal stresses and
are given by:
So, the principal stresses are:
3.2. Principal Strains
To find the principal strains, we solve a similar characteristic equation derived from the strain tensor. For 2D, the principal strains can be found similarly to principal stresses:
Example: consider a 2D strain state with the following components:
The principal strains and
are given by:
So, the principal strains are:
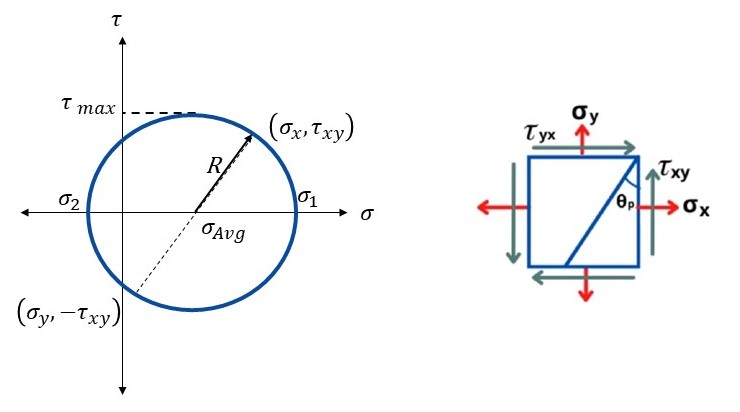
4. Mohr’s Circle
Mohr’s Circle is a graphical representation of the state of stress at a point in a material. It provides a visual method to determine principal stresses, principal strains, and maximum shear stresses. The circle is constructed using the normal and shear stress components on different planes, allowing us to visualize how these stresses transform as the orientation of the plane changes.
4.1. How to draw Mohr’s Circle
Mohr’s Circle simplifies the complex equations involved in stress transformation by providing a geometric explanation. Here’s a step-by-step explanation of how Mohr’s Circle is used to find principal stresses and strains:
- Plot the Points:
- For a given stress state, plot two points on the stress plane (
).
- Point A represents the normal stress
and shear stress
on the x-plane.
- Point B represents the normal stress
and shear stress
on the y-plane.
- For a given stress state, plot two points on the stress plane (
- Determine the Center and Radius:
- The center of Mohr’s Circle, C, is the average normal stress:
.
- The radius of the circle, R, is the square root of the sum of the squares of half the difference of normal stresses and the shear stress:
.
- The center of Mohr’s Circle, C, is the average normal stress:
- Draw the Circle:
- Using the center and radius, draw the circle. This circle represents all possible normal and shear stresses on different planes through the point.
- Find Principal Stresses:
- The principal stresses
and
are found at the points where the circle intersects the horizontal axis (
).
-
(major principal stress) is at the rightmost intersection.
-
(minor principal stress) is at the leftmost intersection.
is at the highest point of the circle.
- Also, Maximum shear stress is calculated by:
.
- The principal stresses
Figure 4: Drawing Mohr’s Circle
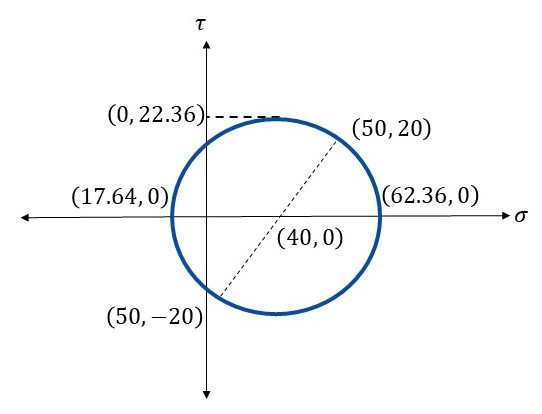
Example: consider the stress state:
Step 1: Plot points A and B:
- Point A (
): (50, 20)
- Point B (
): (30, -20)
Step 2: Determine the center and radius:
Step 3: Draw the circle with center C and radius R.
Step 4: Find the principal stresses:
Figure 5: Example of drawing Mohr’s Circle
4.2. Principal Strains using Mohr’s Circle for Strain
Mohr’s Circle can also be used to determine principal strains in a similar manner. The procedure involves plotting the normal strains and shear strain
to construct the circle and find the principal strains at the intersection points with the horizontal axis. The relations for calculating the parameters of the Mohr’s Circle strain are as follows:
4.3. Benefits of Using Mohr’s Circle
- Visualization: Provides a clear graphical representation of stress transformation.
- Simplicity: Simplifies the complex calculations involved in stress analysis.
- Comprehensiveness: Simultaneously shows principal stresses, maximum shear stresses, and their orientations.
- Insight: Helps in understanding the relation between normal and shear stresses and strains.
5. Von Mises stress in Abaqus
Von Mises stress is particularly useful in situations involving ductile materials (such as metals) under complex loading conditions. In the context of finite element analysis (FEA) using Abaqus, Von Mises stress plays a crucial role in evaluating the material’s response to loading. It is used to predict yielding if the material has reached its yield point under the given load conditions. Also, it is used to identify regions in a model where the stress exceeds the material’s yield strength, indicating potential failure.
5.1. Critical Comparison: Von Mises Stress vs. Principal Stresses
- Von Mises Stress: Provides a scalar value representing the equivalent stress state that can be compared directly with the yield strength of the material. It is especially critical for predicting yielding in ductile materials.
In the third lesson of Abaqus for beginners package, there is a simple example of a beam that would help you to simulate concentrated load on it and do a stress analysis to obtain the Von Mises stress one the beam.
- Principal Stresses: Represent the maximum and minimum normal stresses at a point. While they provide valuable information about the stress state, they are not as directly correlated with yielding in ductile materials as Von Mises stress.
According to Figure 2, which illustrates the more precise and conservative behavior of the von Mises criterion compared to the maximum normal stress criterion, in numerous engineering applications, Von Mises stress is considered more critical for assessing yielding, especially in ductile materials. However, principal stresses are also important for understanding the stress state and identifying potential failure modes like cracking in brittle materials.
For example: consider a cylindrical pressure vessel subjected to internal pressure. Using Abaqus, you can perform a finite element analysis to evaluate the stress distribution.
After running a static analysis to compute the stress distribution in the vessel and plotting the Von Mises stress distribution, we can identify regions where the Von Mises stress exceeds the yield strength of the material. So, if:
- The maximum Von Mises stress in the vessel is below the material’s yield strength, the design is considered safe.
- The Von Mises stress exceeds the yield strength, it indicates potential yielding, and the design may need to be modified to reduce stress concentrations.
6. Conclusion
This article focused on Von Mises stress, a crucial concept in engineering used to predict material yielding under complex loading conditions. Understanding Von Mises stress is essential for designing safe and effective structures, especially when working with ductile materials.
The importance of this topic lies in its application within finite element analysis (FEA) using tools like Abaqus, where Von Mises stress is employed to assess whether a material will withstand operational loads. The article covered several key areas: the definition and calculation of Von Mises stress, its role in predicting yielding through the Von Mises criterion, and how it compares to other failure criteria like the Tresca and Rankine criteria. Additionally, it discussed the importance of principal stresses and Mohr’s Circle in stress analysis, providing insight into the stress state at a point in a material.
In conclusion, we learned that Von Mises stress is an important tool in engineering that helps predict material failure, ensuring the safety and reliability of designs. Understanding its calculation, application, and comparison to other criteria allows engineers to make informed decisions in the design process.
The CAE Assistant is committed to addressing all your CAE needs, and your feedback greatly assists us in achieving this goal. If you have any questions or encounter complications, please feel free to share it with us through our social media accounts including WhatsApp.
Of course you can always learn more in detail about Abaqus in Abaqus Documentation.
If you need deep training, our Abaqus Course offerings have you covered. Visit our Abaqus course today to find the perfect course for your needs and take your Abaqus knowledge to the next level!

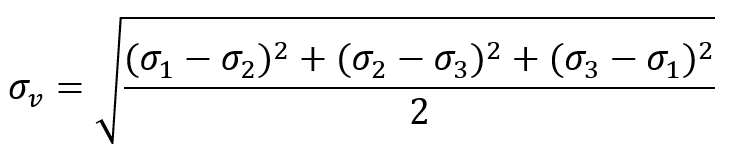
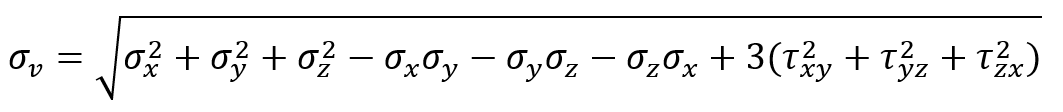
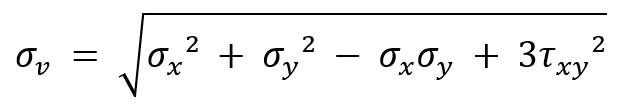

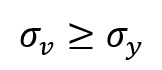
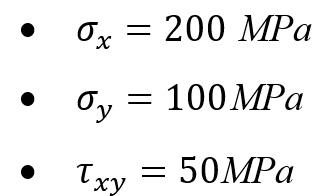
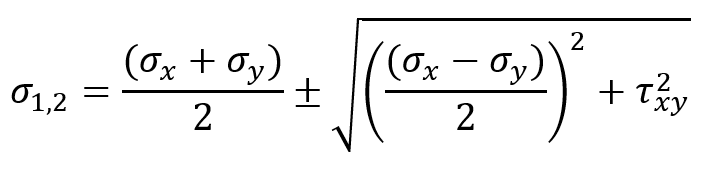
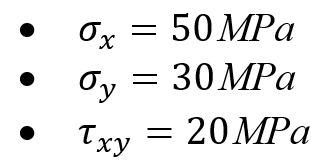
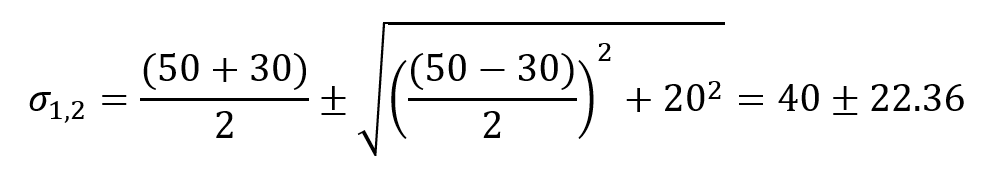
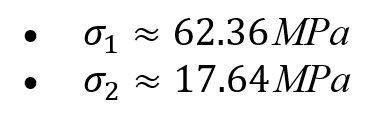
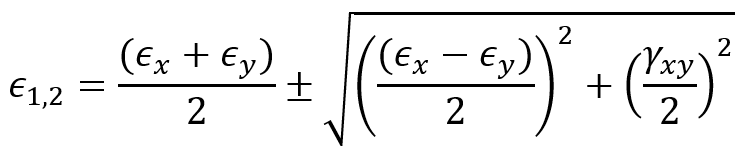
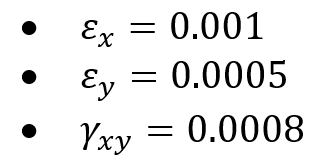
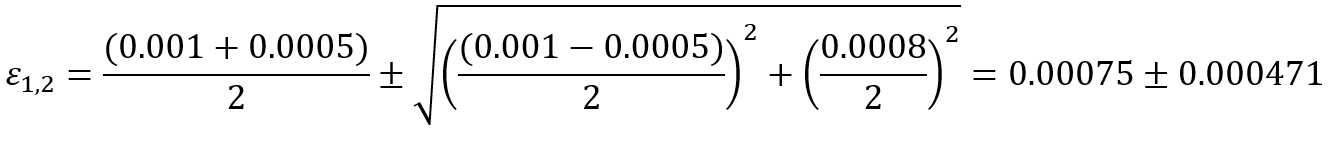
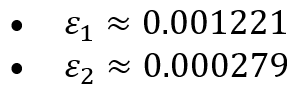
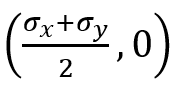 .
.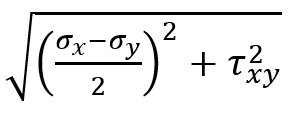 .
.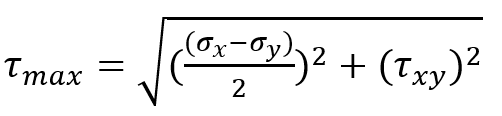 .
.