Automatic Stabilization Abaqus of Unstable Problems | dissipated energy fraction, Damping factor

1. Locally unstable problems (Automatic stabilization Abaqus)

What is the Automatic stabilization Abaqus used for in the ABAQUS standard? Can we use it in unstable problems? How can I stabilize an unstable quasi-static analysis? How can I stabilize a problem in ABAQUS/Standard?

2. Introduction to Unstable Problems in Finite Element Analysis

When it comes to simulating real-world scenarios using finite element analysis, not all problems are created equal. In fact, some problems can be downright unstable, leading to inaccurate results and frustrating simulations. Unstable problems in finite element analysis refer to those that exhibit non-convergent or oscillatory behavior, making it difficult to obtain reliable solutions. These types of problems are often characterized by nonlinear geometries, complex material behaviors, or large deformations, and can be particularly challenging to solve using traditional finite element methods. In Abaqus, unstable problems can manifest in a variety of ways, including non-convergence of the solution, overflow or underflow errors, or even crashes. To overcome these challenges, engineers and analysts need a robust and reliable approach to stabilize these unstable problems, ensuring that accurate and meaningful results are obtained. This is where automated stabilization in Abaqus comes into play, offering a powerful tool to tackle even the most recalcitrant simulations.

3. What is automatic stabilization in Abaqus? | Automatic stabilization Abaqus

Imagine a model on the verge of collapse. Tiny imbalances in the calculations can send it spiraling into numerical oblivion. Automatic stabilization acts like a metaphorical shock absorber, adding a touch of damping to the system. This controlled energy dissipation helps the solver navigate these instabilities and reach a solution.

Nonlinear static problems can become unstable due to geometry (like buckling) or material issues (like softening). When instability causes a negative stiffness in the global load-displacement response, it’s treated as a buckling or collapse problem. But if the instability is localized, strain energy transfers locally, and global solutions may fail. These problems need to be solved dynamically or with artificial damping, like using dashpots.

Abaqus/Standard offers an automatic way to stabilize these quasi-static problems by adding volume-proportional damping to the model. This damping can be constant throughout a step or vary with time to adapt to changes. The adaptive approach is generally better.

The automatic stabilization option in a static general step in Abaqus is a feature that can be used to stabilize unstable quasi-static problems. Abaqus/Standard uses an adaptive automatic damping algorithm to add volume-proportional damping to the model. The damping factors can be constant over the duration of the step, or they can vary with time to account for changes over the course of a step. The latter, adaptive approach is typically preferred (Automatic stabilization Abaqus).

Abaqus automatic stabilization is useful for a variety of problems, such as:

• Contact problems with large amounts of friction
• Post-buckling problems
• Problems with large deformations
• Problems with material softening
• Problems with multiple load steps that involve significant changes in the stiffness of the model

Automatic stabilization is not turned on by default. To activate it, the user must explicitly specify the STABILIZE parameter in the *STATIC step definition. The user can also specify the damping factor directly or allow Abaqus to calculate it based on a dissipated energy fraction.

4. Methods of Automatic Stabilization in Abaqus

Abaqus provides three main methods to automatically stabilize static problems (Automatic Stabilization Abaqus):

4.1. Constant Damping Factor

• This method adds viscous forces to the global equilibrium equations to stabilize the problem.
• The damping factor is constant throughout the step.
• Must be specified for each step as it does not carry over automatically.
• Suitable for cases where the problem is stable at the beginning but may develop instabilities.

Other tips:

• Activation: This method is triggered by including automatic stabilization in any nonlinear quasi-static procedure.
• Mechanism: It introduces viscous forces of the form  into the global equilibrium equations, where is an artificial mass matrix calculated with unity density, c is a damping factor, and is the vector of nodal velocities with  being the time increment.
• Mass Matrix Calculation: For Timoshenko beams, the mass matrix is always calculated assuming isotropic rotary inertia.
• Step-by-Step Activation: Automatic stabilization needs to be explicitly declared for each step where it’s required. Abaqus recalculates new damping factors for each step based on the solution of the first increment.
• Continuation: If the instabilities have not subsided by the end of a step, viscous forces may be terminated abruptly or modified, potentially causing convergence issues. In such cases, restarting the analysis with the damping factor from the previous step is recommended.

4.2. Damping Factor Based on Dissipated Energy Fraction:

• This method calculates the damping factor based on the energy dissipated during the first increment of a step.
• Assumes the problem starts stable and applies damping if instabilities arise.
• The default dissipated energy fraction is 2.0 × 10⁻⁴, but this can be customized.
• If the first increment is unstable, damping is applied from the start to stabilize the solution.

Other tips:

• Energy-Based Calculation: This method calculates the damping factor based on the dissipated energy fraction, which is a small fraction of the extrapolated strain energy, typically set at a default value of 2.0 × 10⁻⁴.
• Initial Stability Assumption: It assumes that the problem is stable at the beginning of the step. As instabilities develop, local velocities increase, and part of the strain energy is dissipated by the applied damping.
• Time Increment Adjustment: Abaqus can reduce the time increment to allow the process to occur without causing large displacements due to instability.
• Custom Fraction: Users can specify a non-default dissipated energy fraction for automatic stabilization.
• First Increment Handling: If the first increment is unstable or singular, damping is applied during this increment. The damping factor is then recalculated based on the energy method if the solution indicates stability.

4.3. Adaptive Automatic Stabilization:

• The damping factor varies spatially and with time, adjusting based on the convergence history and energy ratios.
• More effective for complex models, such as thin shells, where a constant damping factor might not be suitable.
• The default accuracy tolerance is 0.05, which can be adjusted as needed.
• Provides flexibility by increasing or decreasing the damping factor automatically to maintain stability.

Other tips:

• Adaptive Damping: The damping factor varies both spatially and with time, controlled by the convergence history and the ratio of the energy dissipated by viscous damping to the total strain energy.
• Dynamic Adjustment: Abaqus increases the damping factor in case of problematic convergence due to instabilities or rigid body modes, and reduces it when stability is regained.
• Accuracy Tolerance: The ratio of the energy dissipated by viscous damping to the total strain energy is limited by an accuracy tolerance, which has a default value of 0.05. Users can specify a non-default accuracy tolerance if needed.
• Initial Damping Factor: The initial value of the damping factor is typically the same as for automatic stabilization with a constant damping factor, but additional factors considered in adaptive stabilization may cause differences.
• Direct Specification: Users can directly specify the initial damping factor and adjust it based on convergence history and accuracy tolerance.

These methods ensure that the model remains stable throughout the analysis, adjusting for any instabilities that may arise during the process (Automatic Stabilization Abaqus).

5. Dissipated Energy Fraction in Stabilization | Dissipated Energy Fraction Abaqus

Here are some tips for using automatic stabilization:

• Use the adaptive approach whenever possible.
• Start with a small damping factor and increase it gradually as needed.
• Monitor the stabilization energy (ALLSD) and the total energy (ALLSE) of the model. The stabilization energy should be kept to less than 5% of the total energy.
• Be aware that too much stabilization can cause non-physical behavior or even non-convergence.

Automated stabilization can be used for locally unstable problems. This option will automatically damp your system with three different methods (see Figure 1) to solve convergency issues and make your system stable. It’s like the Maximum displacement option in the RIKS method. Just remember, when you use this option, you have to monitor the damping energy to avoid incorrect results. You must compare the viscous damping dissipated energy (ALLSD) with total strain energy (ALLIE) and ensure they won’t differ more than 2 or 5 percent. See Figure 2; you could specify the mentioned percentages in part shown in the Figure (Dissipated Energy Fraction Abaqus).

Figure 1 three different methods for Automatic stabilization

Figure 2: specify the maximum difference between ALLSD and ALLIE

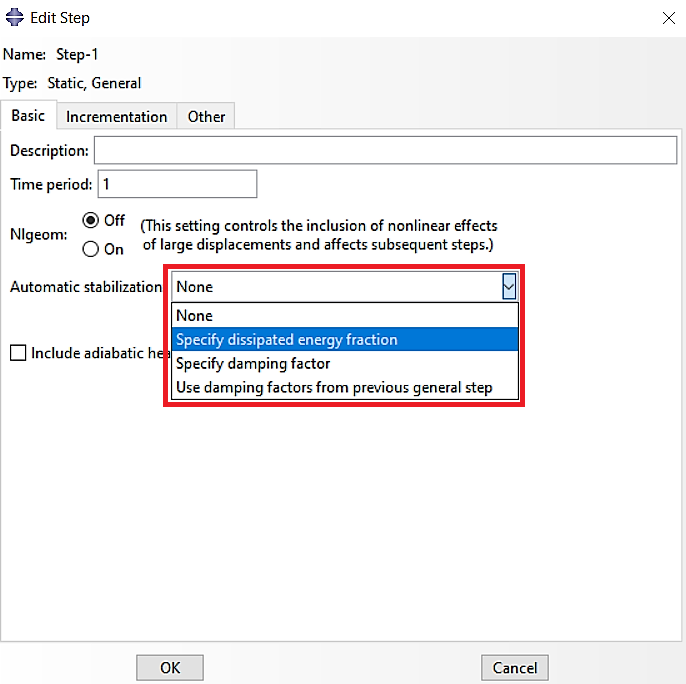
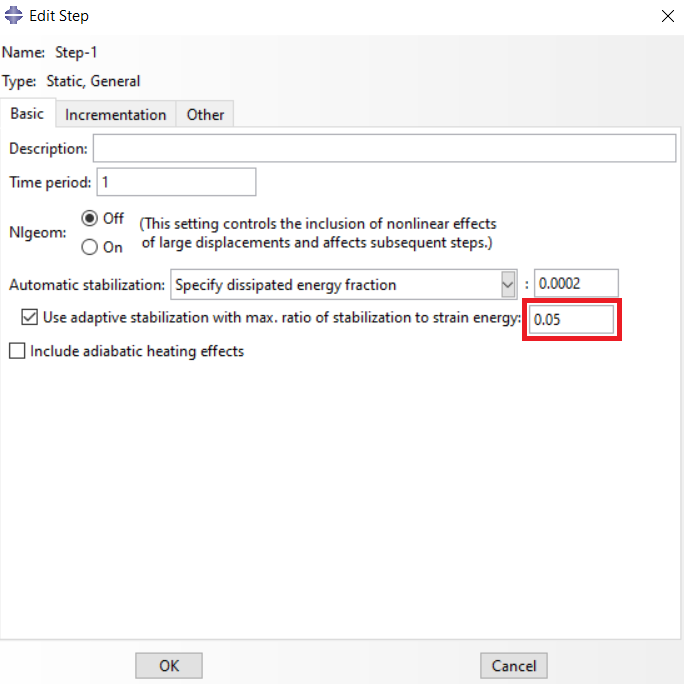
This concept could sometimes be tricky and needs practice; so I recommend the Abaqus Documentation as well to overcome the convergence issues.

Also, you can learn all about Abaqus Nonlinear Analysis and the Abaqus Convergence issues, respectively in the blogs below:

Abaqus nonlinear analysis VS linear analysis

Abaqus convergence issues in simple terms | FEA convergence problem

Explore our comprehensive Abaqus tutorial page, featuring free PDF guides and detailed videos for all skill levels. Discover both free and premium packages, along with essential information to master Abaqus efficiently. Start your journey with our Abaqus tutorial now!