What are Abaqus Hybrid Elements? | Abaqus common element errors

Did you know that Abaqus hybrid elements can effectively handle incompressible materials? Hybrid elements are designed to overcome the limitations of traditional displacement-based elements by introducing an additional degree of freedom, pressure, which independently represents the volumetric component of stress. This feature is crucial for accurately simulating incompressible or nearly incompressible materials, such as rubber and biological tissues.

Hybrid elements are essential when dealing with nearly incompressible materials, high-pressure applications, geotechnical simulations, or problems exhibiting severe volume locking. Alongside, excessive rotation of elements is a common issue in Abaqus, often occurring during large deformations or contact interactions, and can lead to numerical instability. To address these, one must refine the mesh, adjust time increments, modify contact properties, and ensure appropriate material models.

In this blog, we will cover:

• Abaqus Hybrid Elements: Understanding their purpose and application.
• Incompressible Elements in Abaqus: When and why to use them.
• Using Hybrid Elements in Abaqus: Step-by-step instructions.
• Excessive Rotation of Elements: Identifying causes and solutions.
• Gravity Load and Discrete Elements: Assigning density to discrete elements. By the end, you’ll gain practical insights into using hybrid elements and addressing excessive rotation issues in Abaqus.

1. What is Abaqus Hybrid Elements?

To overcome the limitations of traditional displacement-based elements for incompressible materials, Abaqus offers hybrid elements. These elements introduce an additional degree of freedom, pressure, to independently represent the volumetric component of stress.

In incompressible or nearly incompressible materials (where the Poisson’s ratio is close to 0.5), traditional displacement-based finite element methods can lead to numerical instability and volumetric locking. Hybrid elements introduce an independently interpolated pressure stress variable, coupled to the displacement solution through the constitutive theory and compatibility conditions using a Lagrange multiplier. This method effectively removes the singular behavior and prevents locking by ensuring that the pressure stress is accurately represented as a basic solution variable, allowing the elements to handle the incompressibility constraint more effectively.

2. Incompressible Elements in Abaqus

Incompressible Elements refer to elements used in the simulation of materials that do not change volume under pressure. These materials have a Poisson’s ratio close to 0.5. Common examples include rubber and biological tissues. In standard finite element formulations, incompressibility can cause numerical issues such as volumetric locking, where the elements become overly stiff and yield inaccurate results.

3. When to use Hybrid elements?

You should use hybrid elements in Abaqus when dealing with:

1. Nearly Incompressible Materials: Materials with a Poisson’s ratio approaching 0.5, such as rubber, biological tissues, and some plastics.
2. High-Pressure Applications: Scenarios where the material is subjected to high pressure and is expected to maintain its volume.
3. Geotechnical Simulations: Where soil or other materials exhibit incompressible behavior under certain conditions.
4. Problems exhibiting severe volume locking: When standard elements produce inaccurate results due to excessive stiffness.

4. How to use Hybrid elements in Abaqus?

To use hybrid elements in Abaqus, follow these steps:

1. Element Type Selection:

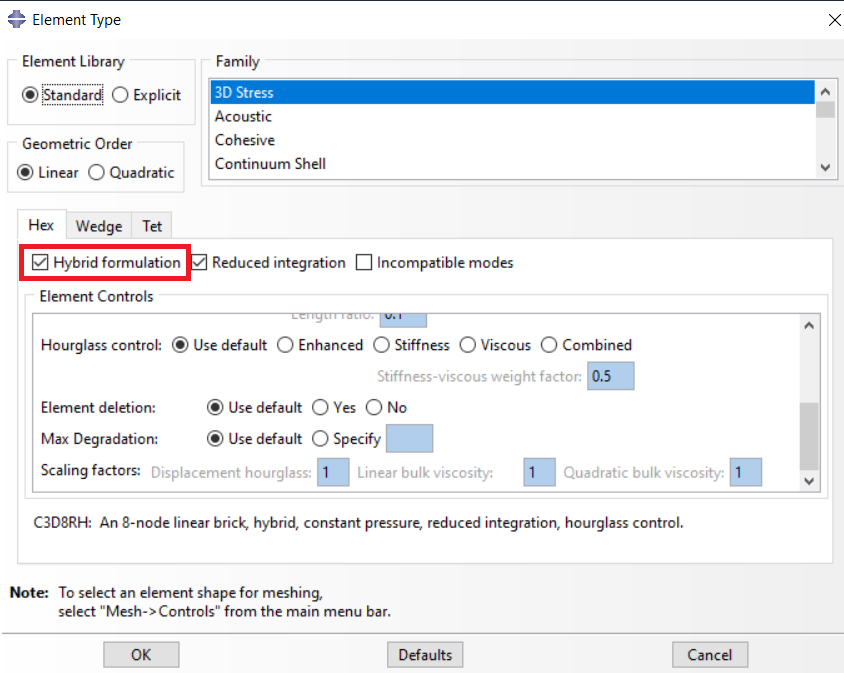
In the Element Type dialog box, look for element names containing the letter “H”. These are hybrid elements. For example, C3D8H is a hybrid 8-node hexahedral element.  

2. Material Definition:

Define the material properties appropriately, including Poisson’s ratio. For incompressible materials, Poisson’s ratio is typically 0.5.  

3. Mesh Generation:

Create a suitable mesh using the selected hybrid element type.

4. Boundary Conditions and Loads:

Apply boundary conditions and loads as usual.

5. Solver Settings:

The Hybrid formulation is only available in ABAQUS/Standard.

See the Figure below; you can use a Hybrid formulation through the “Assign Element Type”.

Figure 1: How to use Hybrid formulation in Abaqus

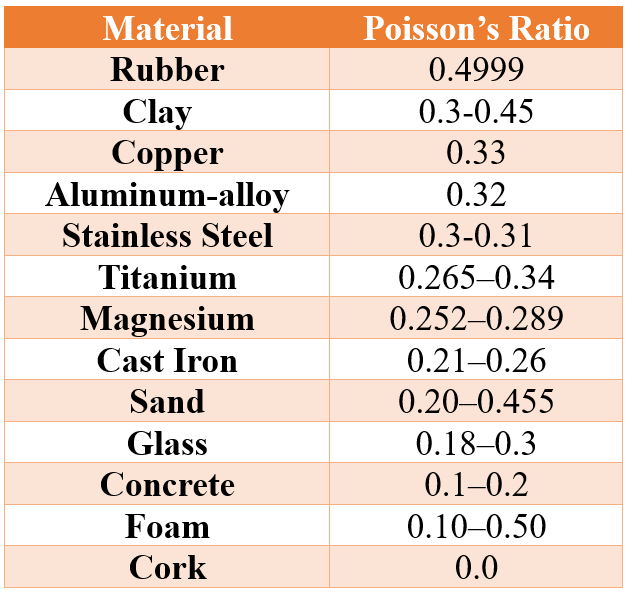
4.1. Poisson’s ratios of common materials

Poisson’s ratio spans from -1 to 0.5. A material is termed auxetic if its ratio is below 0. When a positive strain is applied along the longitudinal axis, the transverse strain also becomes positive, leading to an increase in the cross-sectional area.

Common metals like steel and aluminum typically have Poisson’s ratios between 0.2 and 0.35, making them compressible. In contrast, materials such as rubber and certain foams have a ratio of 0.5, rendering them incompressible.

Table1: Poisson’s Ratio of common materials [read more]

5. What is excessive rotation of elements in Abaqus?

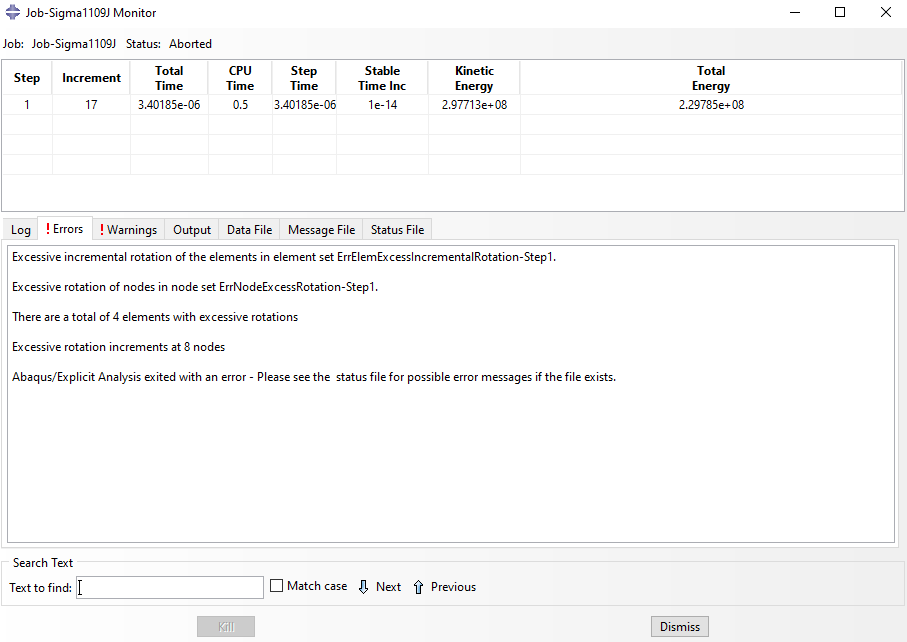
Excessive rotation of elements in Abaqus typically occurs when elements undergo significant distortion during the analysis. This can lead to numerical instability and premature termination of the simulation. It’s often associated with large deformations, contact interactions, and explicit dynamics simulations.

Abaqus will show you this error:

Figure 2: Excessive rotation of elements

5.1. When do we get this error?

• Large deformations: The error often occurs during simulations involving large deformations or rotations, such as metal forming processes or dynamic impact analyses.
• Time increment issues: It can happen when the time increment is too large, causing elements to rotate excessively between steps.
• Mesh-related problems: Poorly structured or overly coarse meshes may lead to this error.
• Contact problems: In some cases, excessive rotations can be triggered by contact overclosures or other contact-related issues.

5.2. How to fix it?

We have some recommendations for you. Of course, there could be more but here are the general ones:

1. Refine the Mesh:

• Reduce element size in critical areas where large deformations or contact interactions occur.
• Use appropriate element types for the problem (e.g., reduced integration elements for shells).
• Check element quality metrics to identify and improve poorly shaped elements.

2. Adjust Time Increment (Explicit Dynamics):

• Reduce the time increment to allow for smaller deformations per step.
• Use automatic time stepping with appropriate minimum and maximum time increments.

3. Modify Contact Properties:

• Adjust contact stiffness or damping to improve contact behavior.
• Consider using different contact formulations (e.g., penalty, augmented Lagrangian).
• Check for contact penetration and adjust tolerances if necessary.

4. Employ Mass Scaling (Explicit Dynamics):

• Increase the mass of the model to reduce the critical time step, but use it cautiously as it can affect results.

5. Consider Alternative Formulations:

• Explore different element formulations (e.g., hybrid elements).
• Use ALE (Arbitrary Lagrangian-Eulerian) or Eulerian formulations for severe distortions.

6. Check Material Models and Properties:

• Ensure material models and properties are appropriate for the analysis.
• Verify that material parameters are correctly defined.

7. Monitor Energy Balance:

• Check for excessive kinetic or internal energy, which may indicate numerical issues.

6. Gravity load and discrete elements

I received an error while performing discrete element analysis in Abaqus “NO ELEMENT IN THE MODEL HAS MASS FOR APPLICATION OF GRAVITY LOAD.  MATERIAL DENSITY MAY HAVE NOT BEEN SPECIFIED”. How to assign density to the discrete elements?

First, you must define a reference point for your discrete model; then, define the mass on the reference point.

As we have understand, some of our errors in Abaqus can be solved by meshing; but how to do a right meshing? Learn that with this professional package:

Different Techniques for Meshing in Abaqus

You can learn mesh and meshing in Abaqus from the very beginning to advanced level with this package.

7. Conclusion

This article examined the use of Abaqus Hybrid elements to address issues with incompressible materials and excessive rotation of elements. Hybrid elements were introduced as a solution for numerical instability and volumetric locking in nearly incompressible materials by incorporating an additional pressure degree of freedom. The importance of hybrid elements was highlighted for materials with a Poisson’s ratio close to 0.5, high-pressure applications, and geotechnical simulations. The process of using hybrid elements in Abaqus was outlined, including element type selection, material definition, and solver settings.

The issue of excessive rotation in elements, often due to large deformations or time increment issues, was discussed with recommendations for fixing it, such as refining the mesh, adjusting time increments, modifying contact properties, and employing mass scaling. The article concluded with the resolution of errors related to gravity loads in discrete elements by defining a reference point and assigning mass.

This comprehensive guide provided valuable insights into effectively managing hybrid elements and resolving excessive rotation issues in Abaqus simulations.

8. References

1. https://classes.engineering.wustl.edu/2009/spring/mase5513/abaqus/docs/v6.6/books/stm/default.htm?startat=ch03s02ath61.html
2. https://classes.engineering.wustl.edu/2009/spring/mase5513/abaqus/docs/v6.6/books/usb/default.htm?startat=pt03ch06s03at07.html

Explore our comprehensive Abaqus tutorial page, featuring free PDF guides and detailed videos for all skill levels. Discover both free and premium packages, along with essential information to master Abaqus efficiently. Start your journey with our Abaqus tutorial now!