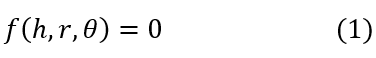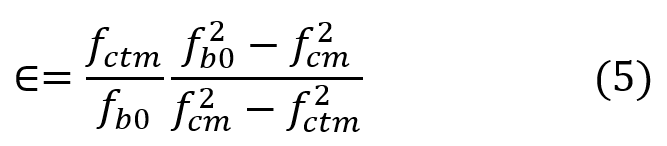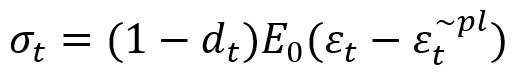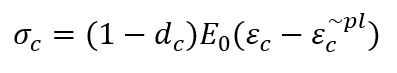Concrete Damage Plasticity (CDP) in Abaqus

Modeling the behavior of concrete under various loading conditions is a significant challenge in structural engineering due to the material’s anisotropic and quasi-brittle nature, exhibiting different responses under tensile and compressive stresses. To accurately understand and predict the nonlinear behavior of concrete, the use of advanced numerical models is essential. One of the most powerful models for simulating this behavior is the Concrete Damage Plasticity (CDP) model in Abaqus. The CDP model combines concepts of plasticity and damage to simulate the cracking, softening, and gradual deterioration of concrete under different loading scenarios. This model enables engineers and researchers to predict the complex behavior of concrete more accurately in various structural projects and achieve more optimal designs.
In this article, we aim to simplify the complex process of modeling concrete behavior for you. To do so, we will highlight the challenges involved, such as accurately capturing the material’s anisotropic and quasi-brittle nature, and provide clear insights into using the Concrete Damage Plasticity (CDP) model In Abaqus.
1. Nonlinear Behavior of Concrete
Concrete is a composite material that displays complex behavior under various types of loading due to its heterogeneous nature. Its nonlinear characteristics stem mainly from the presence of cracks, voids, and the interactions among its components, including aggregates, cement paste, and water. Gaining insight into this nonlinear behavior is essential for accurately predicting how concrete structures will behave under different stress scenarios, such as:
- Compression: Concrete demonstrates high strength under compression, but once a certain stress threshold is exceeded, it begins to show nonlinear behavior, marked by cracking and crushing.
- Tension: Concrete is relatively weak under tensile stress, where its nonlinear response is largely governed by the initiation and spread of cracks.
- Shear: Nonlinear behavior in shear arises from the interaction between cracks and the interlocking of aggregates.
Additionally, factors such as loading rate, temperature, moisture levels, and the presence of reinforcement significantly influence the nonlinear behavior of concrete.
Accurately predicting the nonlinear behavior of concrete under various loading conditions is essential for ensuring the performance and safety of structures. This behavior can be analyzed using two common methods: experimental and numerical. While experimental methods provide valuable insights, they also present challenges such as high costs, time requirements, and complexity. As a result, numerical methods have become increasingly popular. However, these methods also have their own set of challenges. In this article, we will address these challenges and demonstrate how to effectively use the Concrete Damage Plasticity (CDP) model in Abaqus, a leading tool for the numerical analysis of concrete structures.
2. The Role of Numerical Methods in Analyzing the Nonlinear Behavior of Concrete
Numerical simulations play a key role in understanding and predicting the nonlinear behavior of concrete. Some of the important numerical methods used are discussed in the following.
2.1. Finite Element Method (FEM)
The finite element method involves dividing the structure into multiple parts. It can simulate crack development and interaction, non-uniform stress distribution, and the effects of various loading conditions in concrete structures.
2.2. Discrete Element Method (DEM)
DEM is particularly effective for simulating concrete behavior at the meso-scale, where interactions between aggregates can be examined. DEM models each particle separately, making it useful for simulating fracture and crack propagation.
2.3. Lattice Models
These models represent concrete as a network of interconnected elements, effectively simulating the process of crack formation and propagation. They are well-suited for studying the failure process in concrete.
2.4. Cohesive Zone Models (CZM)
CZM is used to model the fracture process where material separation occurs at a specific interface. This method is useful for simulating the initiation and controlled growth of cracks.
2.5. Multiscale Modeling
Multiscale modeling is not an independent method but is a common technique used within the framework of other methods. It integrates models at different scales (micro, meso, macro) to provide a comprehensive understanding of concrete behavior.
| Explore our comprehensive Abaqus tutorial page, featuring free PDF guides and detailed videos for all skill levels. Discover both free and premium packages, along with essential information to master Abaqus efficiently. Start your journey with our Abaqus tutorial now! |
3. Using Abaqus for the Analysis of Concrete Behavior
In Abaqus software, three types of cracking can be modeled to account for concrete nonlinear behavior, which can be defined in the Abaqus edit material window:
1- Smeared Crack Concrete Model
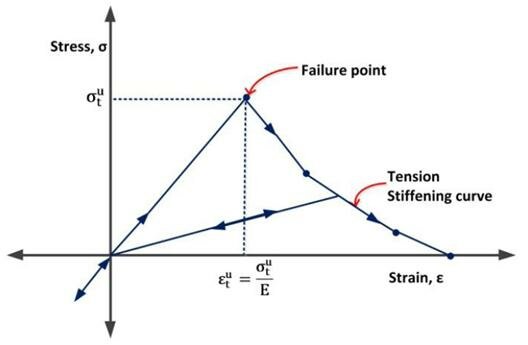
This method is designed for situations where concrete experiences primarily monotonic strain under low confinement pressures. It features an isotropically hardening yield surface, along with a separate crack detection mechanism. The post-failure tensile behavior in this method is modeled with tension stiffening, as shown in Figure 1.
Figure 1: Tension stiffening model [1]
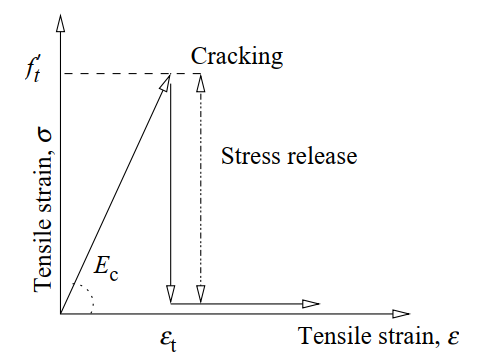
2- Brittle Crack Concrete Model
Despite concrete being quasi-brittle, it is often treated as brittle for simplicity. The “brittle crack concrete model” is a theoretical and computational framework used to analyze concrete structures under stress, focusing on crack formation and propagation.
Figure 2: Brittle Crack Concrete [2]
3- Concrete Damage Plasticity Model
The most renowned and precise criterion for examining the nonlinear behavior of concrete is the Concrete Damage Plasticity Model. This model takes into account two main assumptions in the failure mechanism: tensile cracking and compressive crushing. We will explain this important criterion in detail below.
4. Abaqus Concrete Damage Plasticity Model
The failure criterion in the plastic range of the material is expressed under combined stresses. This criterion is divided into two main categories based on the material’s response to hydrostatic pressure. In most materials, ductile behavior is known as hydrostatic pressure-dependent, and non-metallic materials such as soil, rocks, and concrete belong to this category and are pressure-dependent.
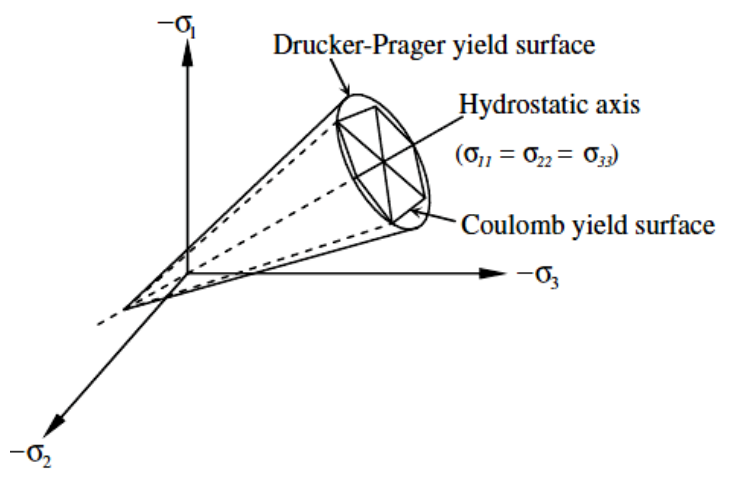
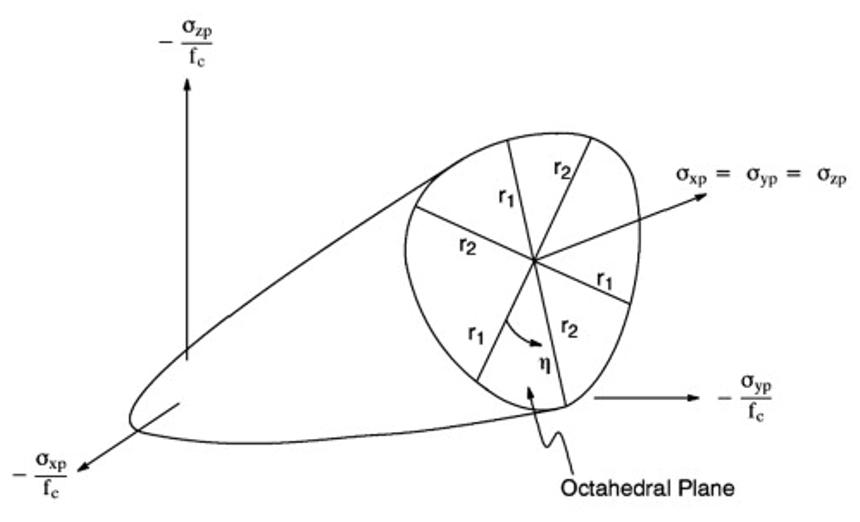
When discussing the Abaqus Concrete Damage Plasticity Model, the failure potential function is derived from the Drucker-Prager model for concrete behavior. The main formulation of the plastic potential surface in the CDP model is represented by Equation 1, and the three-dimensional shape of the deviation from the stress planes is shown on the meridian planes, as presented in Figure 3.
Figure 3: Drucker-Prager model [3]
The principles of failure, introduced by Kachnov in the mid-1950s, were based on the reduction of stress surfaces. Since then, the failure mechanism has been considered based on degradation models and is currently evaluated using the secant of damage softening.
Degraded models consider the elastic stiffness degradation as the total damage. For concrete, this behavior is defined based on the degree of confinement of the element. When the confinement is low due to the loading process, damage occurs rapidly and is irreversible. Conversely, if the confinement is high, more time is needed for damage to develop when the load is applied. The formula for the elastic damage softening model in scalar dimension d is given by Equation 2.
4.1. Implementation of CDP model in Abaqus CAE
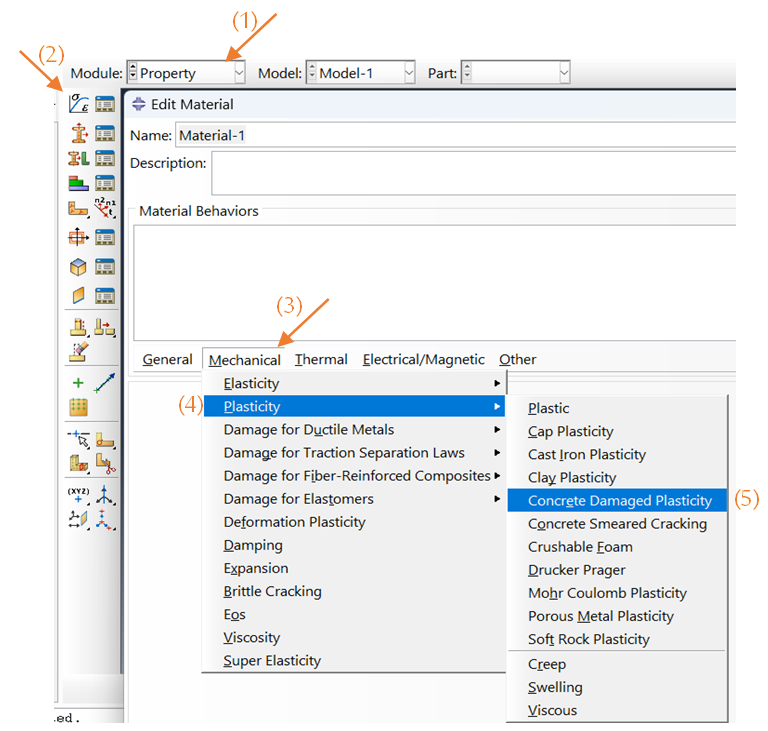
To use the Concrete Damage Plasticity model in Abaqus, simply go to the Property module and create a new material. In the edit material window, select Mechanical. Then click on Plasticity. Now, you can select the Concrete Damage Plasticity model. This process is shown in Figure 4.
Figure 4: Implementation of the CDP model in Abaqus
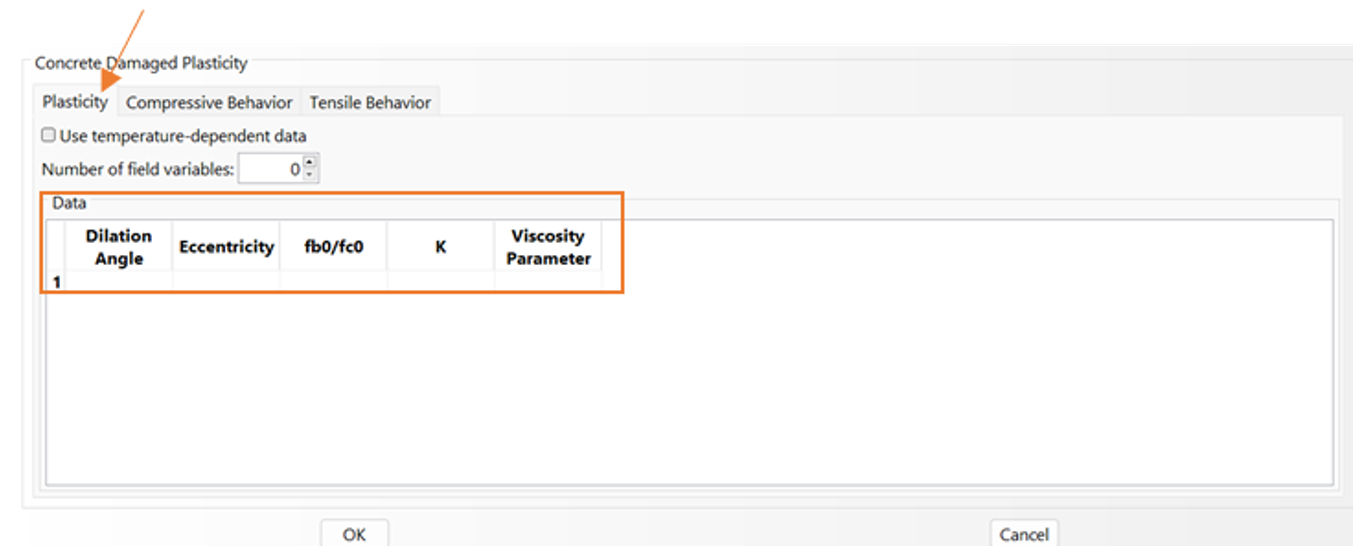
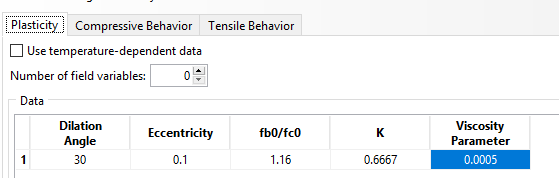
After selecting CDP, in the Plasticity section, you can define the parameters of the Concrete Damage Plasticity model in Abaqus based on the characteristics of the desired concrete. These parameters are explained in the next section, and the corresponding values are provided.
Figure 5: Defining the plasticity data for CDP model in Abaqus
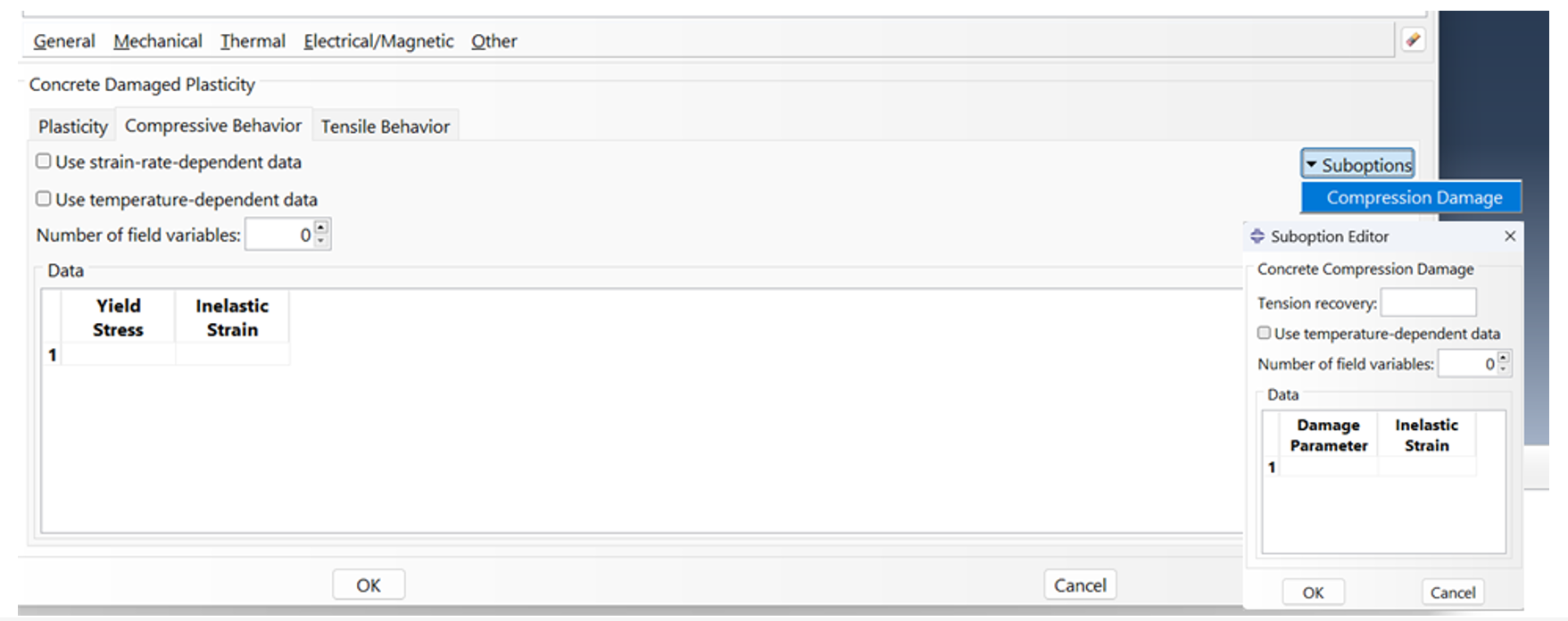
For the Compressive Behavior, as shown in Figure 6, you need to define the compressive stresses and inelastic strains for your model. Additionally, by selecting the Suboptions, you can define the damage based on inelastic strains. In the following sections of the article, we provide a detailed explanation of how to calculate these components and their significance.
Figure 6: Defining the compressive behavior for CDP model in Abaqus
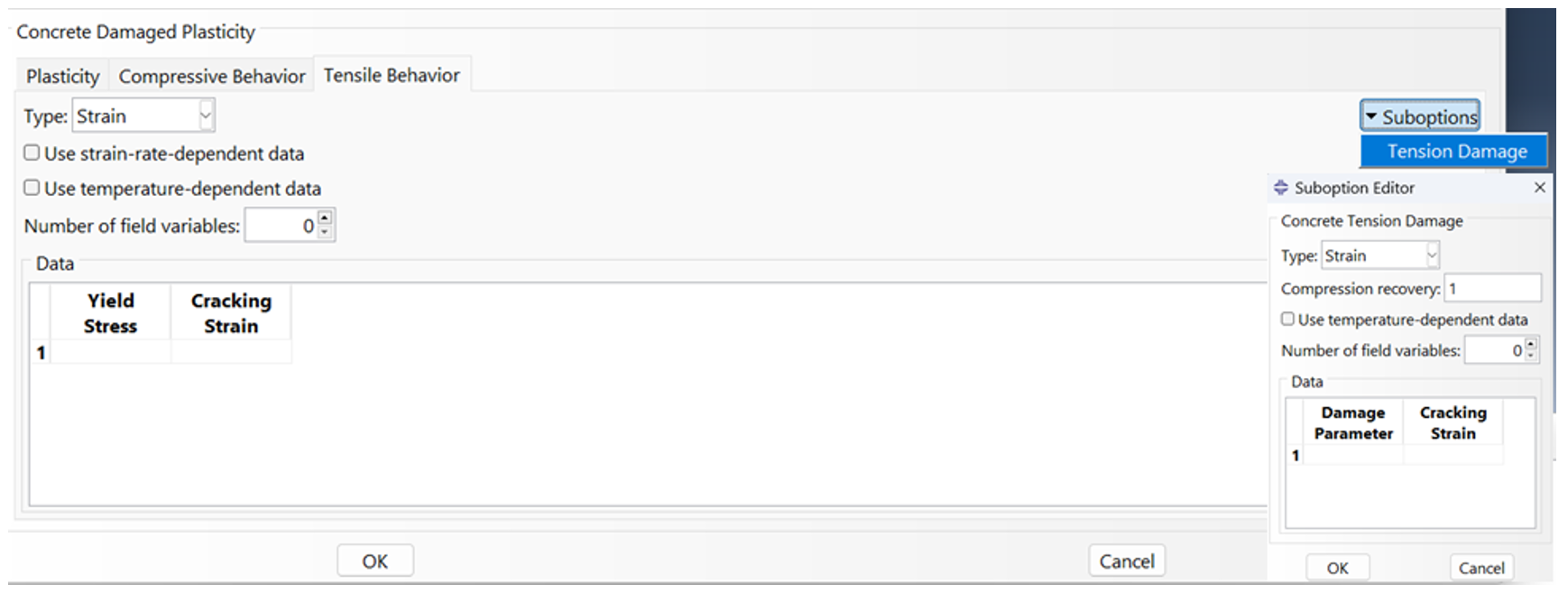
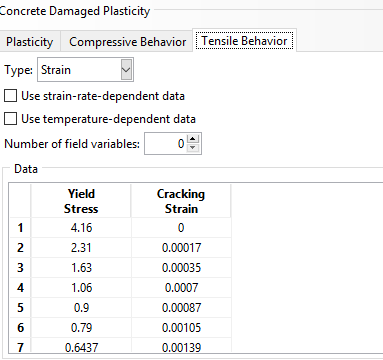
As illustrated in Figure 7, for the tensile behavior, it’s necessary to specify the tensile stresses and cracking strain values for your model. Additionally, you can use the Suboption to define damage based on cracking strains. The upcoming sections of the article offer a comprehensive explanation of how to calculate these parameters and their importance.
Figure 7: Defining the tensile behavior for CDP model in Abaqus
 |
⭐⭐⭐ Free Abaqus Course | ⏰10 hours Video 👩🎓+1000 Students ♾️ Lifetime Access
✅ Module by Module Training ✅ Standard/Explicit Analyses Tutorial ✅ Subroutines (UMAT) Training … ✅ Python Scripting Lesson & Examples |
4.2. Required parameters for CDP Model in Abaqus
To use the Concrete Damage Plasticity (CDP) Model in Abaqus, you need to specify several required parameters. These parameters define the material’s behavior under different loading conditions and are crucial for accurate simulation of concrete behavior. Here are the primary parameters you’ll need to provide:
- Dilation angle
The dilation angle in the p-q plane under high confinement pressure (ψ) describes the plastic strain due to shear stress after the elastic phase. When ψ equals zero, there is no volumetric strain change in the material. Essentially, the dilation angle represents the correlation between volumetric strain and shear strain, as indicated by equation (3). Based on Vermeer and de Borst’s research, materials that are sensitive to hydrostatic pressure, such as rock, soil, and concrete, have a typical dilation angle of about 20°, which exceeds their internal friction angle, typically around 12°, under multiaxial stress conditions. If confinement occurs, the dilation angle may vary. Studies indicate that for reinforced concrete, the dilation angle can range from 20° to 40°. A smaller dilation angle results in more brittle material behavior, while a larger angle leads to behavior resembling that of ductile materials. A dilation angle of ψ = 31° has been identified as optimal for defining concrete behavior in both compression and tension scenarios.
- Eccentricity
The parameter m denotes the eccentricity of the plastic potential surface, as determined by Bazant and Jirasek. Using equations (4) and (5), the values for are calculated for concrete with a compressive strength of
.
The default flow potential eccentricity is 0.1, which implies that the material has almost the same dilation angle over a wide range of confining pressure stress values. Values of m that are significantly less than the default value may lead to Abaqus convergence issues if the material is subjected to low confining.
- The ratio of biaxial to the uniaxial compressive yield stresses
This parameter describes the characteristics of the failure function and is defined by . It is the ratio of initial equibiaxial compressive yield stress to initial uniaxial compressive yield stress (the default value is 1.16. Most sources suggest values of 1.16 and 1.25, depending on the strength of the concrete and the degree of confinement.
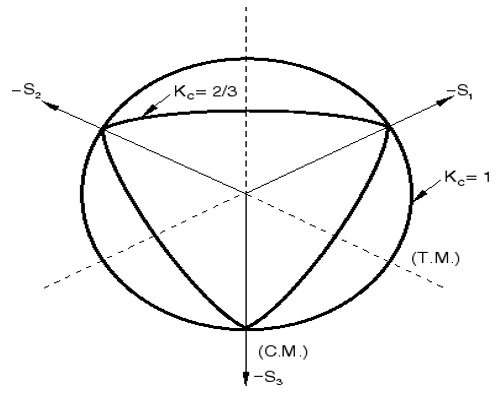
- The ratio of the second stress invariant on the tensile meridian to that on the compressive meridian(
)
This parameter characterizes both the configuration of the deviatoric stress plane and the confinement angle of concrete. A triangular shape of the deviatoric plane indicates a lower level of confinement, while a circular shape suggests a higher degree of confinement.
Figure 8: Yield surfaces related to different values [4]
The parameter is typically set between
and 1, though some researchers propose a maximum value of 0.8 the default value is
.
- Viscosity parameter
In advanced material models, achieving convergence when dealing with tensile stresses and stiffness degradation often presents difficulties. A standard method to address this problem is to employ viscoplastic regularization equations. These equations estimate the tangent stiffness of the material by accounting for its softening behavior.
Abaqus uses the Duvaut-Lions regularization approach, which applies relative strain tensors for modeling viscosity-related stiffness degradation. Using the viscoplastic regularization with a small value for the viscosity parameter (small compared to the characteristic time increment) usually helps improve the rate of convergence of the model in the softening regime, without compromising results. In ABAQUS/Standard, the default value of the viscosity parameter is zero, so that no viscoplastic regularization is performed.
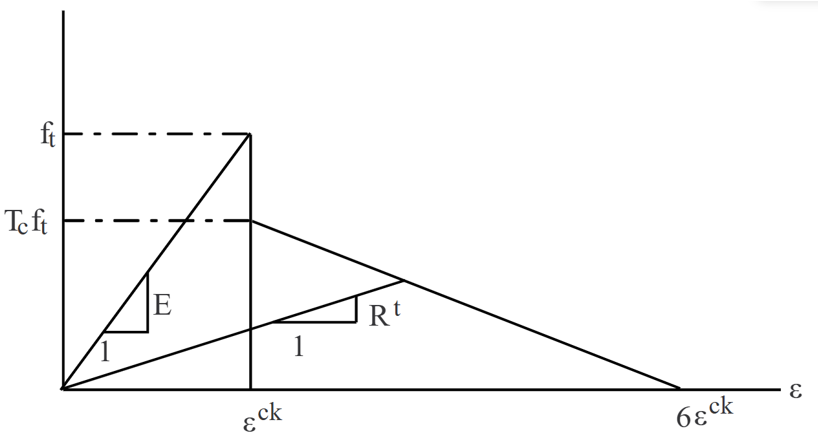
4.3. CDP Model | Nonlinear Tensile Behavior
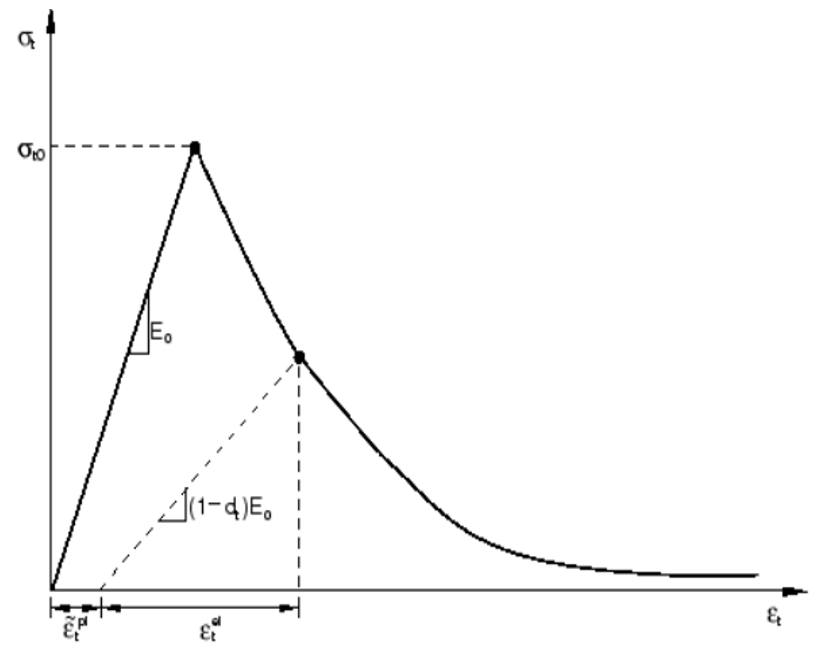
To fully model the tensile behavior of concrete in Abaqus, the post-failure stress-strain behavior for tension is considered. This behavior is obtained through strain softening, as shown in Figure 9. To define such behavior in Abaqus, the values of Young’s modulus , stress
, cracking strain
, as well as the damage parameter
, which ranges from zero to one, must be input for the specific concrete class. The cracking strain is obtained from the following equation:
is the elastic strain corresponding to the undamaged material, and
is the total tensile strain.
As shown in Figure 9, when the concrete specimen is unloaded from any point on the strain-softening branch of the stress-strain curve, a weakened unloading response is observed: the elastic stiffness of the material appears to be damaged (or degraded). The degradation of elastic stiffness differs significantly between tension and compression tests; in both cases, the effect becomes more pronounced as plastic strain increases.
The degradation of the elastic stiffness is characterized by the damage variable . The damage variables can take values from zero, representing the undamaged material, to one, which represents total loss of strength.
According to the presented rules, if is the initial (undamaged) elastic stiffness of the material, the stress-strain relation under tensile loading is as follows:
Figure 9: Concrete tensile model [4]
4.4. CDP Model | Nonlinear Compressive Behavior
Nonlinear compressive behavior refers to the way that concrete and similar materials respond under compressive loads in a non-linear manner. Initially, concrete behaves elastically, but as the load increases, it starts to exhibit non-linear characteristics such as plastic deformation and strain softening. With high compressive forces, damage and cracking develop, leading to reduced stiffness and load-bearing capacity. Beyond a specific point, concrete undergoes permanent deformation, further decreasing its ability to support loads and its stiffness. Accurate modeling of this nonlinear behavior is essential for precise structural analysis and design.
To define the compressive stress-strain behavior of concrete in Abaqus, the stress values , the corresponding inelastic strains
, and the damage properties
must be input according to Figure 10. The total strain values can be converted into inelastic strains from the following equation:
where is the elastic strain corresponding to the undamaged material, and
is the total compressive strain.
The degradation of the elastic stiffness in CDP model is characterized by the damage variable . The damage variables can take values from zero, representing the undamaged material, to one, which represents total loss of strength.
If is the initial (undamaged) elastic stiffness of the material, the stress-strain relation under compression loading is as follows:
Figure 10: Response of concrete to uniaxial loading in compression [4]
 |
Abaqus basic tutorials on concrete beams and columns Syllabus: 1. Finite element modeling and simulation of concrete beam
2. Finite element modeling and simulation of concrete beam reinforced with steel bars and stirrups
3. Finite element modeling and simulation of concrete beam reinforced with fiber reinforced polymer
|
 |
Fiber Reinforced Concrete Beams | An Abaqus Simulation syllabus: 1. Introduction | An Overview of Fiber Reinforced Composites
|
 |
|
 |
Ultra-High-Performance Fiber Reinforced Concrete (UHPFRC) structures in Abaqus Syllabus: |
5. Cracking analysis in concrete
The main challenge in the design and analysis of concrete structures arises from crack growth and concrete crushing. They may occur under tensile, shear, or compressive stresses. However, as the compressive strength of concrete is several times greater than its tensile strength, compressive crushing is less likely to occur. As a result, tensile and shear cracks are more commonly observed in concrete members. So, cracking analysis in concrete is an important aspect of engineering. Figure 11 illustrates how cracking in a concrete structure can reduce its service life. In light of this significance, several theories have been developed for cracking analysis in concrete. In the following sections, we will explore some of these theories that are incorporated into widely used CAE software.
Figure 11: Cracking in a concrete specimen [Ref.]
To account for the low tensile strength of concrete and to prevent cracking, we use steel rebars, which help carry tensile loads. Nevertheless, cracking analysis in concrete is still necessary to determine where cracks occur, how they propagate, and whether they are tensile or shear cracks. This helps us design plain or reinforced concrete structures accurately.
In general, we have two types of cracks in concrete specimens:
- Tensile cracks
- Shear cracks
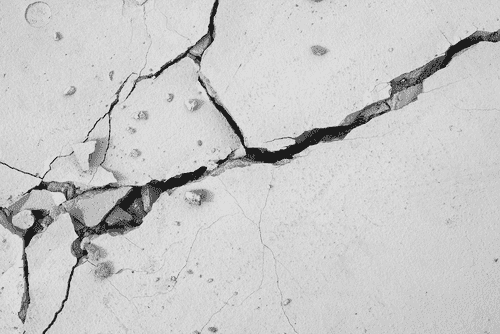
Both tensile and shear cracks are probable in concrete specimens. However, tensile cracks are relatively easy to predict, while shear cracks are more difficult to anticipate. Moreover, shear cracks can lead to sudden failures of structures, often without prior warning or visible signs. Accordingly, cracking analysis in concrete remains a challenging topic in engineering fields. We have compared tensile and shear cracks in figure 12 for a better understanding.
Figure 12: Comparison of shear and tensile cracks in concrete [Ref.]
According to the figure, tensile cracks generated as a result of normal stress act perpendicular to the crack plane. They may form in specimens subjected to direct tension or flexural loads, as shown in Figure 13.
Figure 13: Tensile cracks in concrete under direct tension [Ref.]
As shown in Figure 12, Shear cracks often form in concrete beams (flexural members) near the supports. These cracks typically angle between 30° and 45° to the beam’s axis, extending from the tension face of the member towards the support. They occur when two sections slide relative to each other, causing a separation that leads to cracking.
We have several common approaches for cracking analysis in concrete within CAE software. For example, we can refer to the Concrete Damage Plasticity or Smeared Crack models in Abaqus, the Willam-Warnke model (Solid65) in Ansys APDL, the Winfrith Concrete Model in LS-DYNA, or the Chang and Mander Model in OpenSees. These models calculate stiffness or strength reduction at each integration point and plot the damage variable or stiffness reduction. This allows us to predict crack locations and their paths based on stiffness and strength degradation.
We have discussed the CDP and Smeared Crack models in the first sections of the paper. The other mentioned models are very similar to CDP, as they also feature a yield surface. For example, the yield surface for the Willam-Warnke model is presented in figure 14.
Figure 14: The yield surface for the Willam-Warnke model
The model considers a proposed failure criterion based on the stress states to predict whether a material point has failed. Note that, to account for tensile cracks in the model, we have a reduction rule, as presented in figure 15.
Figure 15: Reduction rule in Ansys APDL software for the tensile behavior of concrete
One of the advantages of Ansys APDL over similar models is the ability to input the percentage of reinforcement, facilitating the cracking analysis in concrete with steel rebars. All other mentioned models use similar rules for the cracking analysis in concrete structures. The following table briefly summarizes the benefits of using each model for cracking analysis in concrete in various CAE software.
Figure 16: Comparison of different models for cracking analysis in concrete in various CAE software
5.1. Specimens with preexisting cracks
Consider a concrete specimen with preexisting cracks. The goal is to continue loading and perform further cracking analysis in concrete. Using the mentioned models is not sufficient in this case, as they have limitations in defining preexisting cracks. To address this issue in Abaqus, you can use the XFEM or VCCT models to define an initial crack. Afterward, the CDP model can be used to predict crack propagation. This approach demonstrates how CAE software like Abaqus has simplified cracking analysis in concrete, whether for existing or newly generated cracks.
Remember, the concrete damage plasticity can be applied on any concrete structures and most of all columns and beams. You can learn all about concrete columns and beams in this blog: “Concrete Column Analysis + Beams Explained: Design, FEA“.
6. Conclusion
Given concrete’s inherent anisotropic and quasi-brittle nature, understanding its nonlinear response to tensile and compressive stresses is crucial for effective structural engineering. The Concrete Damage Plasticity (CDP) model in Abaqus provides a robust framework for accurately simulating the complex behavior of concrete under various loading conditions. The CDP model integrates principles of plasticity and damage to capture the nuances of cracking, softening, and deterioration, thus offering valuable insights into concrete behavior.
Through this article, we have outlined the challenges of modeling concrete’s nonlinear behavior, emphasizing the significance of advanced numerical methods. The Concrete Damage Plasticity model stands out for its ability to simulate both tensile and compressive responses accurately, accommodating the material’s complex failure mechanisms and degradation under different stress conditions. By leveraging such advanced modeling techniques, structural engineers can achieve more reliable predictions and optimal designs, ensuring the safety and performance of concrete structures across diverse applications.
Here we have presented some users questions about CDP or concrete damage plasticity:
I. CDP analysis
Q: I used the CDP model to create a small solid cubical part. After establishing the necessary boundary conditions, the load is applied. When I check at the stress in my odb file, some of the elements have more stress than the yield stress I entered? Is there an explanation for this?
A: Two things could have happened; either you didn’t enter the CDP parameters correctly, such as units might be wrong or anything else, or when you defined the compressive and tensile behavior, you didn’t control the slope of the diagrams.
Check the link below. In these lessons, you will understand the CDP completely.
Abaqus Tutorial for Beginners (Abaqus Tutorial for Civil Engineering)
II. Concrete Damage Plasticity Abaqus simulation
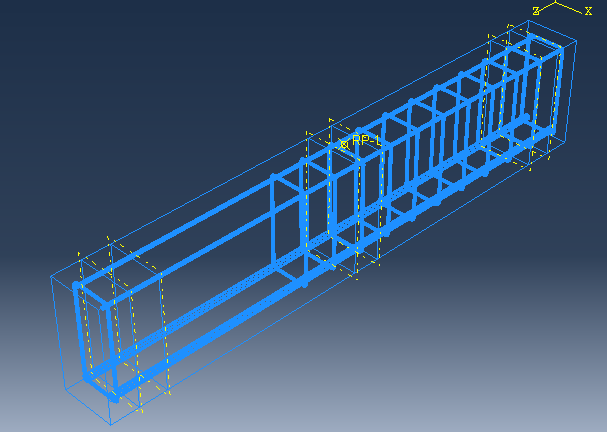
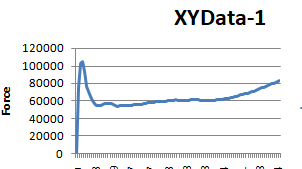
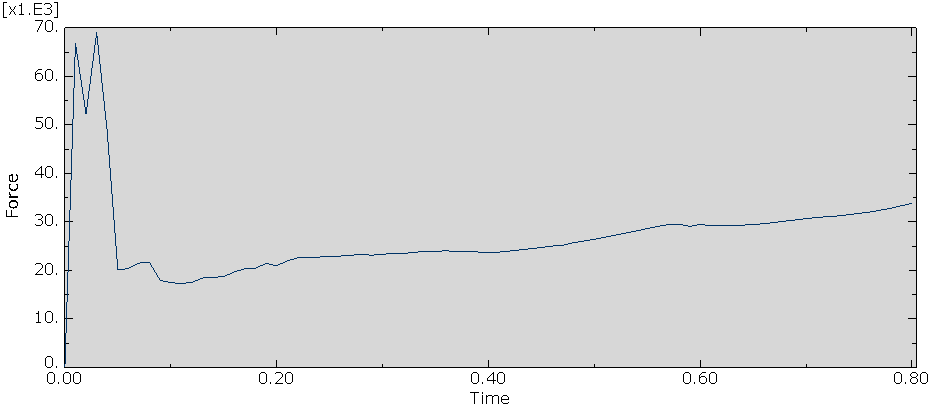
Q: In the Concrete Damage Plasticity Abaqus simulation, I’m working with fiber concrete. I had previously modeled the EN 14651 (3-point bending) test and now I was testing my “real” beams. She has longitudinal reinforcement and stirrups, as seen in the photo (figure 1). There are no stirrups in a small test area (I’m dealing with shear). However, regardless of how the material input stresses change, the force-displacement graphs in the post-peak zone show increasing force (Figures 2 and 3).
The supports were positioned in a beam region (without drawing the supports) and the displacement was applied in an RP with “coupling.” Reinforcement can also be found in the “embedded region.” I put it to the test with some random material from a YouTube video, and the strength keeps increasing. Is there something wrong with my model? In addition, the peak force is significantly higher than the experimental data. Figures 4 and 5 show the data from the CDP.
Figure 1
Figure 2
Figure 3
Figure 4
Figure 5
A: First of all, you cannot enter random material from a YouTube video and expect to get similar results to the experimental ones. The data you enter must match the ones in the experimental test.
Second, you need to check the data you use is True or engineering and must match the experimental data. If the stress data is True, the diagram you obtained might be correct.
The last thing I recommend is checking the input data units and rechecking your model; you might have done something wrong. I suggest referring to the link below as well. It might help you a lot.
Abaqus Tutorial for Beginners (Abaqus Tutorial for Civil Engineering)
III. Concrete damaged plasticity (CDP) model in Abaqus
Q: I created a CDP model with enlarged boundary elements for a shear wall. I performed a nonlinear static analysis with a 500 mm displacement. I couldn’t observe any difference in results when I increased the amount of longitudinal reinforcement in enlarged boundary elements (column). I mean that the longitudinal bar confinement effect is not visible.
How do I get the confinement effect of ties while modeling an RCC column in Abaqus?
A: I don’t know how you increased the column reinforcement. I suggest rechecking your model. Please note that increasing the number of the bars and decreasing their cross-section simultaneously could cause them to counteract each other’s effect; therefore, the stress won’t change. If that’s what you did, you should change one of them or if you want to change both, do it properly to see its effects in your model.
The CAE Assistant is committed to addressing all your CAE needs, and your feedback greatly assists us in achieving this goal. If you have any questions or encounter complications, please feel free to share it with us through our social media accounts including WhatsApp.
If you need deep training, our Abaqus Course offerings have you covered. Visit our Abaqus course today to find the perfect course for your needs and take your Abaqus knowledge to the next level!
Of course you can always learn more in detail about Abaqus in Abaqus Documentation.