Here, we have a special package for Foam Simulation in Abaqus using subroutines:
Foam simulation in Abaqus
€ 159.0
Foam is a type of expanded plastic and rubber produced by forcing gas bubbles into a polymer material. It is a permeating, lightweight material. Along with corrugated packaging, foam fabric can protect goods during transportation. Foams, a novel family of ultra-light materials, have the capacity to undergo significant deformation at practically constant plateau stress, which allows them to absorb a significant amount of kinetic energy. In this tutorial package, you will learn how to analyze sandwich panels with an interior layer of foam, Foam-Filled Aluminum Tubes subjected to compressive loads, simulation of a reinforced foamed concrete beam, concrete-titanium foam panel explosion, etc. All of these cool practical examples with their complete tutorial videos are in this package which you can read their description below.
| Expert | |
|---|---|
| Included |
.inps,video files, Fortran files (if available), Flowchart file (if available), Python files (if available), Pdf files (if available) |
| Tutorial video duration |
152 minutes |
| language |
English |
| Level | |
| Package Type | |
| Software version |
Applicable to all versions |
Frequently Bought Together
What is Foam material?
Gas bubbles are injected into a polymer substance to create foam, an inflated plastic and rubber material. It is a permeable, light substance. Foam fabric can be used to protect items during transportation in addition to corrugated packaging. With their ability to deform significantly under almost constant plateau stress, foams, a revolutionary family of ultra-light materials, may absorb a substantial amount of kinetic energy. In this foam Abaqus tutorial, some practical examples of foams are presented.
Foams can be used in various sectors like furniture: cushioned fillers in sofa and chair seats, etc. Construction industry: used for sound absorption, thermal insulation, etc. automotive industry: on seats, dashboards, etc. Numerous toys, sponges, footwear, garments, apparel, packaging, and all types of fillings and quilting.
Simulation of Foam materials in Abaqus
In this package, we present you with six workshops to learn how to simulate foam Abaqus materials. You can learn more info about workshops and their simulation detail below.
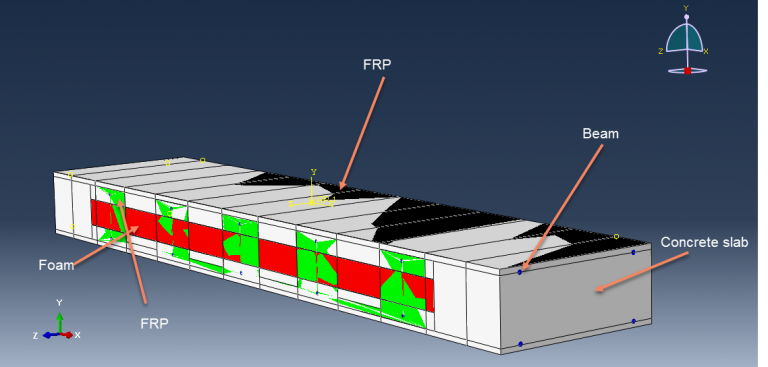
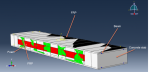
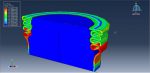
Workshop 1: Blast simulation and damage investigation of insulated concrete sandwich panel
Sandwich panels made of insulated concrete have an interior layer of foam insulation between two outer concrete wythes. Because of their advantages of being lightweight and energy efficient, they are being used more and more. The two outer concrete wythes can be joined together using a variety of shear connections. Fiber-Reinforced Polymer (FRP) shear connectors, which can remove thermal bridging and increase thermal performance, have been adopted more lately. Static and dynamic analyses are typically treated separately in Finite Element (FE) analysis approaches. However, a nonlinear static analysis model would frequently diverge early based on preliminary FE research due to the flexibility of the FRP shear connectors and the concrete cracking in insulated concrete sandwich panels.
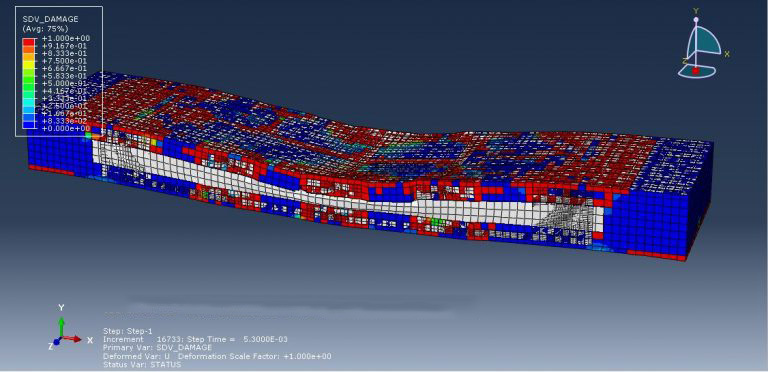
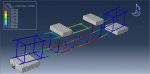
This simulation has looked at insulated concrete sandwich panel blast analysis and damage investigation. Beams are modelled as wire and composite as shell sections, while concrete and foam are represented as three-dimensional solid parts. The Johnson-Cook model for steel, the Crushable foam data for foam, Hashin’s damage criterion for composites, and the Johnson-Holmquist model for concrete are all implied. Below is a diagram showing the assembled parts.
For this kind of analysis, the dynamic explicit and CONWEP air blast procedures are suitable. Because the beams are embedded in the concrete part, the interaction between concrete-foam and concrete composites is regarded as perfect contact. A significant amount of damage was done to the concrete component during the simulation. Under the blast wave, the central portion of the concrete was destroyed, and the foam was entirely compacted. The composite damage criterion is also readily apparent.
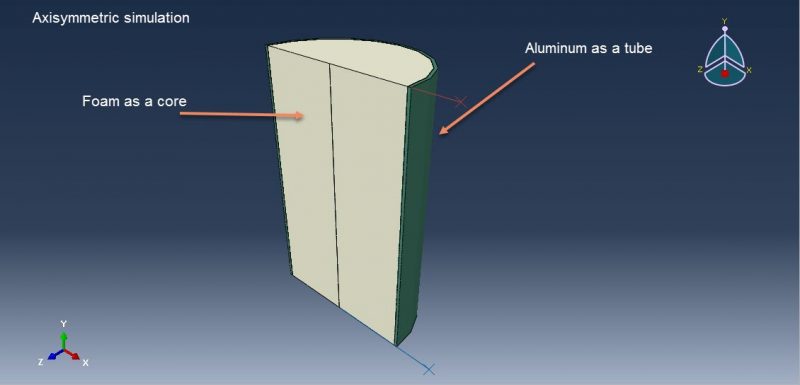
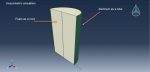
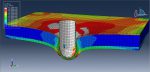
Workshop-2: Crushing Abaqus simulation of foam filled Aluminium tubes
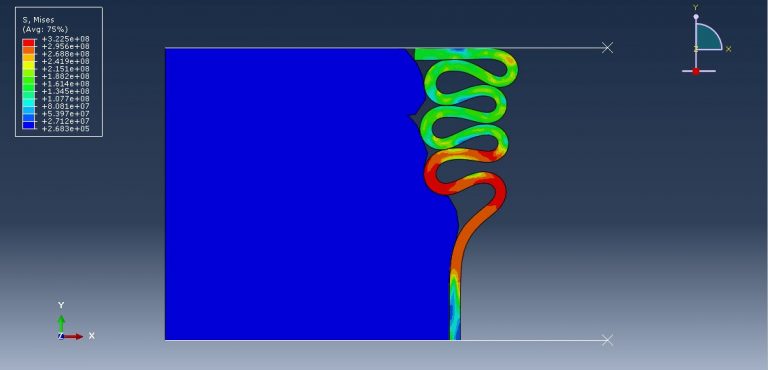
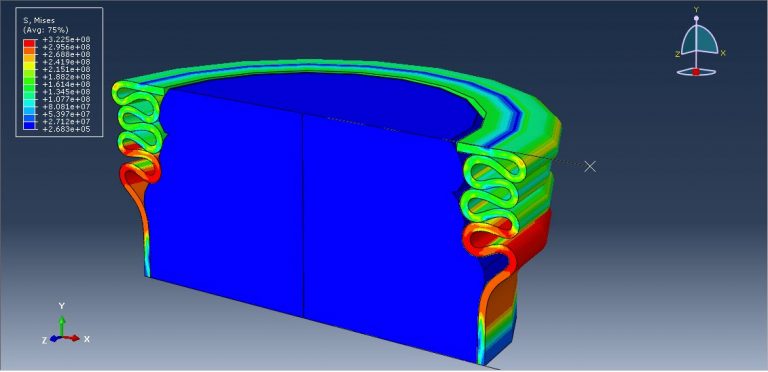
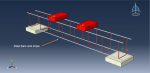
Crushing Simulation of Foam-Filled Aluminum Tubes in Abaqus has been researched in this simulation. Due to their progressive buckling under axial compressive strain and the structure’s lightness, thin-walled metallic tubes have been used as energy absorbers. Previous studies have shown that axisymmetric, also known as concertina or ring mode, non-axisymmetric, also known as diamond mode, or mixed mode, can occur in the collapse of thin-walled circular tubes. The mode in which a tube crush is substantially determined by the tube’s shape. Energy will be absorbed by the structure’s gradual buckling. In this tutorial, foam and aluminium’s three-dimensional behavior is modelled using an axisymmetric dimension. Below is a diagram showing the assembled parts.
Aluminum is employed as an elastic-plastic material, and foam is used as an elastic, crushable foam behavior with hardening. For this kind of investigation, the dynamic explicit technique is appropriate. To specify the interaction between all parts and the self contact for aluminum and foam, the surface to surface contact algorithm is employed. The higher stiff plate is given credit for the displacement. In particular, the mesh needs to be fine for the aluminum to produce the desired outcomes. Aluminum has clearly deformed after the simulation, and all findings are accessible.
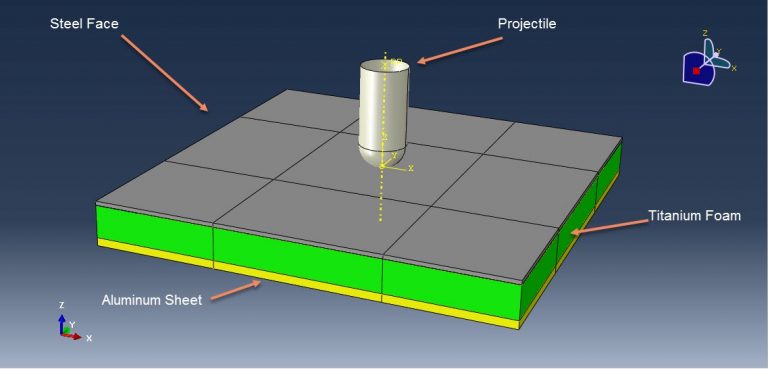
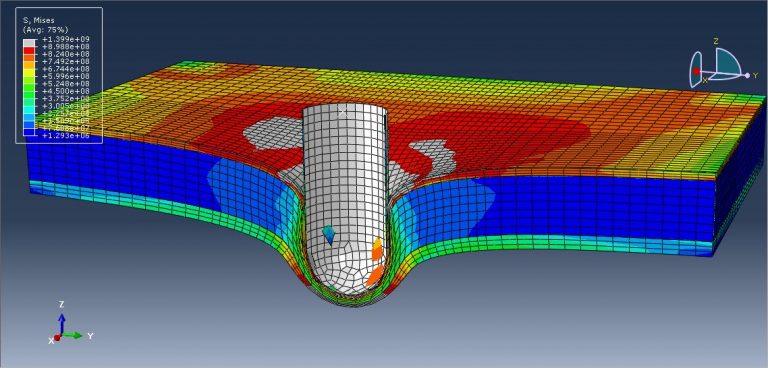
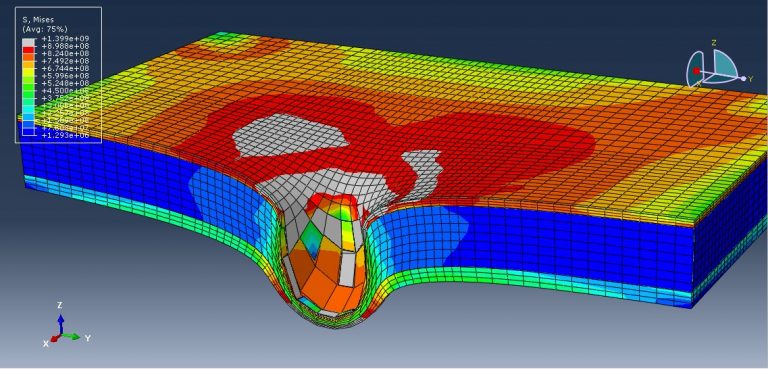
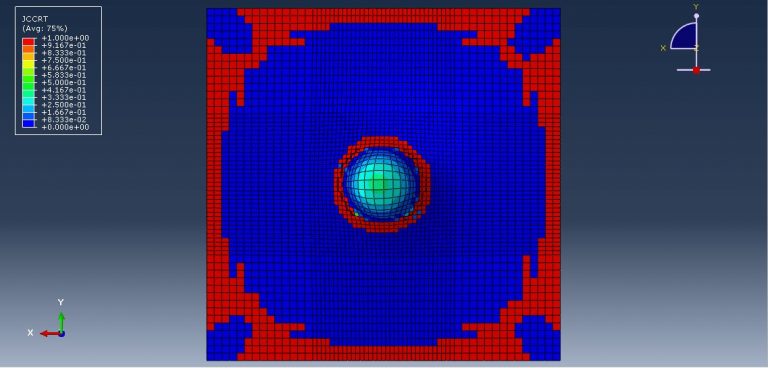
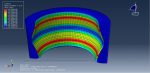
Workshop 3: Dynamic response of square sandwich plates with a metal foam core subjected to rigid projectile impact
This tutorial looks at the dynamic response of square sandwich plates with a metal foam core when they are hit by rigid projectiles in Abaqus. Due to its excellent benefits over the monolithic solid structure of the same mass, the sandwich structure has received increased attention and is frequently employed in a variety of important engineering. The monolithic solid construction has been replaced by the sandwich structure, which has been seen as a promising replacement. The sandwich structure’s structural behavior is influenced by the material’s characteristics as well as the face-sheet, core, and boundary conditions, among other factors. Metal foam is a lightweight material with novel physical and mechanical properties, such as being nearly isotropic, high energy absorption, good sound damping, non-combustibility, easy fabrication to form curved configurations, and integrated face-sheets. It also has high stiffness-to-weight and strength-to-weight ratios. The sandwich structure’s central component is then decided to be the metal foam. The titanium foam, steel, and aluminium are modeled as three-dimensional solid pieces.
The material with elastic-plastic properties (Johnson-Cook) is used for steel plates. Johnson-Cook damage with evolution is used to simulate damage and failure of the steel plate. For the Johnson-Cook plasticity model, which is only appropriate for high strain-rate deformation of metals, Abaqus/Explicit offers a dynamic failure model. The “Johnson-Cook dynamic failure model” is the name of this model. As a member of the family of damage initiation criteria, Abaqus/Explicit also provides a more comprehensive version of the Johnson-Cook failure model, which is the method that is advised for simulating progressive material degradation and failure. Elastic data with crushable foam plasticity isotropic shape and hardening data are employed for titanium foam. Johnson-Cook plasticity and damage are taken into account for the aluminum. The dynamic explicit step is appropriate for this type of analysis. Assumed to be a contact formulation is the general contact algorithm with contact property. Steel and metal foam, as well as aluminum and metal foam, are thought to have the ideal contact. The side surfaces of the panel and the projectile’s starting velocity are both given the fixed boundary condition. Near the contact zone, the mesh should be that fine. In the next workshops, foam Abaqus simulations are also described.
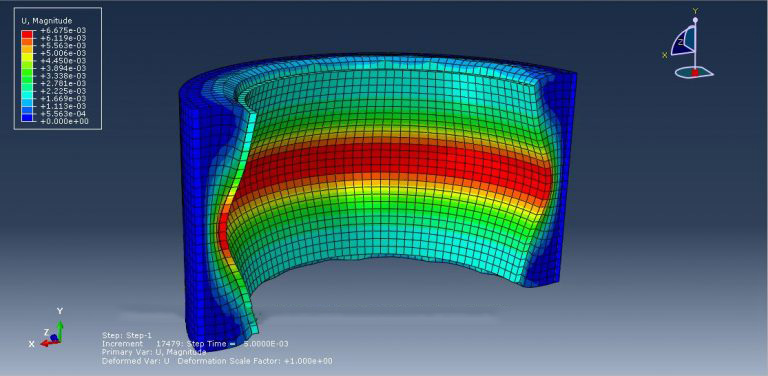
Workshop 4: Numerical simulation of foam-cored sandwich tubes under internal air blast
Foams, a novel family of ultra-light materials, have the capacity to undergo significant deformation at practically constant plateau stress, which allows them to absorb a significant amount of kinetic energy. Due to their outstanding ability to sustain blast loading, foam-cored sandwich structures have drawn increasing interest and have been widely used in maritime and other military applications. Sandwich constructions’ exceptional performances depend on the foam core’s creative geometrical design. Additionally, conventional blast-resistant equipment is bulky and performs poorly. With the rise in terrorism, compact, upgraded blast-resistant containment vessels have gained popularity. The sandwich tube is thought to be a cutting-edge structural design that can improve blast-resistant vessels to hold explosive materials and safeguard people or equipment from an internal explosion. Because sandwich structures may experience extensive plastic deformation at a nearly constant plateau stress, they have a higher energy absorption capacity (EA) than monolithic blast-resistant tubes. Over the past ten years, the dynamic response of sandwich tubes has drawn more and more attention. A representation of the actual item is shown here.
The deformation of tubes and the compaction of foam have been assessed using the Johnson-Cook plasticity for tubes and crushable foam with hardening for foam. This kind of analysis is ideal for dynamic explicit steps. The CONWEP air blast approach was used to suggest blast load over the inside surfaces because the interaction between steel tubes and foam is thought to be ideal. During the analysis, the explosion significantly deforms the interior pipe, which in turn greatly compacts the foam component. (Foam Abaqus)
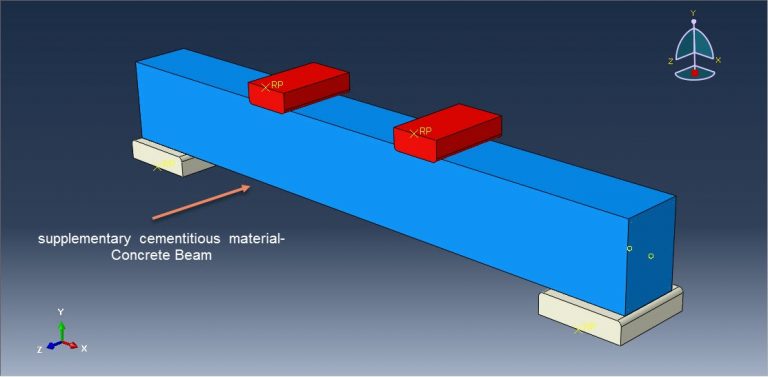
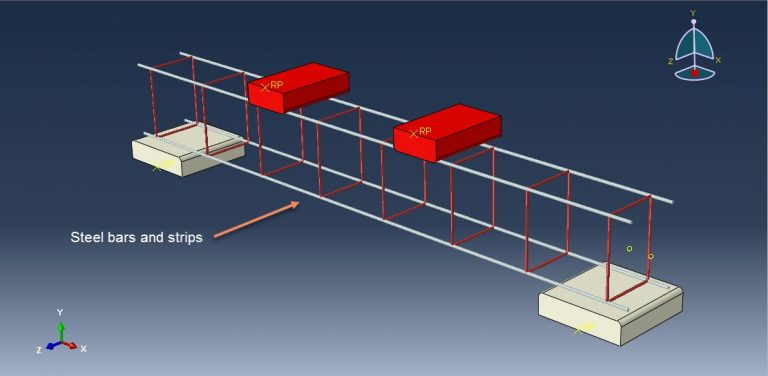
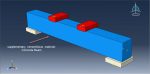
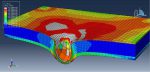
Workshop 5: Four points bending analysis of reinforced foamed-concrete beam containing partial cement replacement
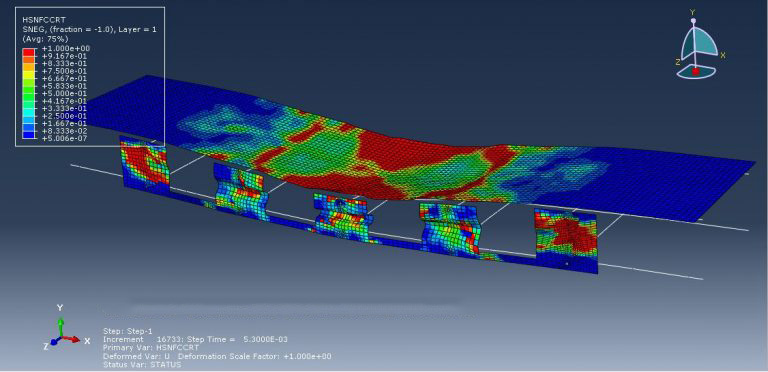
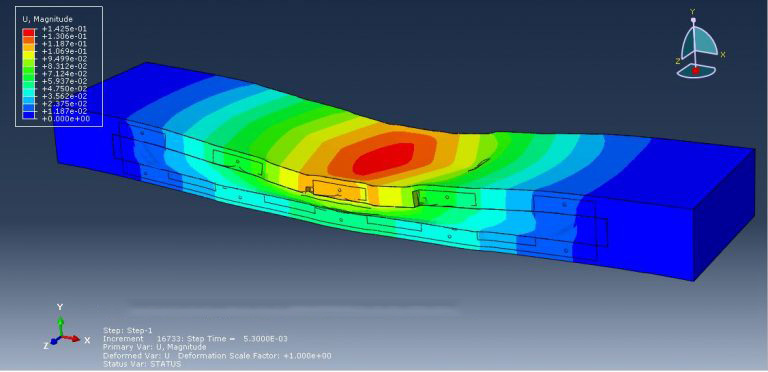
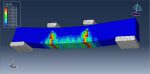
This tutorial has looked at the numerical simulation of a reinforced foamed concrete beam that contains some cement replacement. Concrete-based building materials are currently the main component of structures all over the world. Concrete has a wide range of uses in civil engineering, including the construction of bridges, dams, roadways, and tall buildings. Concrete is in high demand due to its superior strength, durability, and moldability compared to other conventional materials, as well as its relative affordability. Numerous varieties of concrete have been produced ever since the invention of concrete. Concrete foam is one of them. It is a type of lightweight concrete that is up to 87% lighter than regular concrete. Its dry density ranges from 300 to 1800 kg/m3. Sand is used as the fine aggregate in foamed concrete, with cement acting as the binder. All varieties of concrete require cement as a key component because it serves as a binder, holding all other materials together to form a sturdy, stone-like substance. However, there are now environmental worries related to cement production. The concrete beam is modeled as a solid part with three dimensions. The steel bar and strip are represented as wire elements with three dimensions. You can see figures of the assembled parts below.
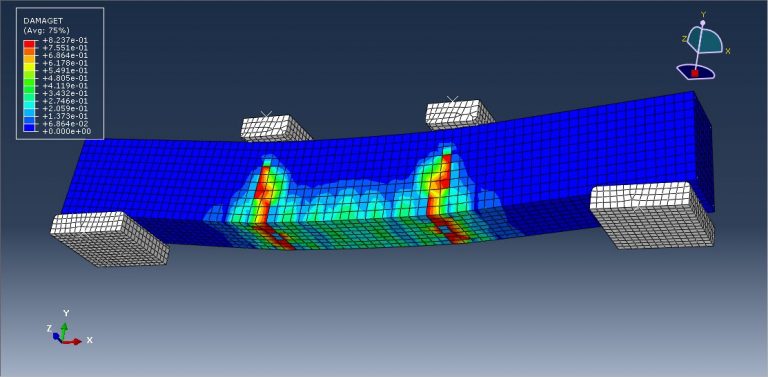
For the concrete beam, the CPD material model is utilized. There are several waste materials that can be used in concrete as SCMs to lessen the need for cement as a binder, though it may take some time to investigate how well such waste materials operate in concrete. In this study, ABAQUS explicit software was used to build a finite element model of a foamed concrete reinforced beam incorporating palm oil fuel ash and eggshell powder (ESP) as a partial cement replacement. For the bars and strips, a steel material with elastic-plastic behavior is used. For this simulation, the general static step with some modifications to the convergence model is appropriate. Surface-to-surface contact with a friction coefficient between rigid bodies and a concrete beam is implied. The concrete beam host contains embedded bars and strips. For the two bottom rigid bodies and displacement for the two top rigid bodies, respectively, the fixed boundary condition is applied. To get good results, the mesh needs to be fine.
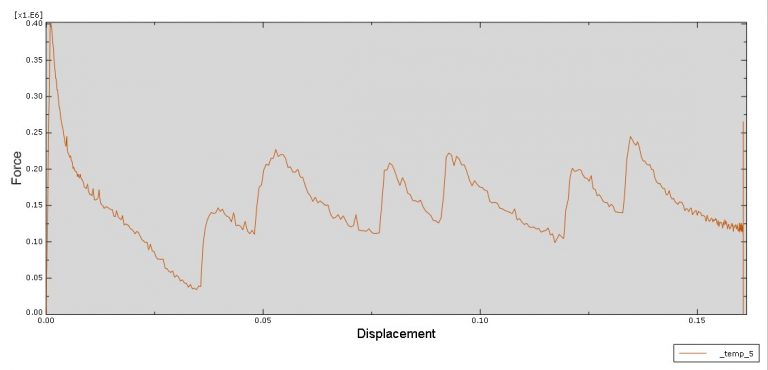
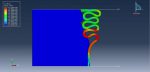
All of the findings, including the force-displacement diagram, and the concrete beam’s stress, strain, tension, and compression damage, are attainable after the simulation. Figures for the outcomes are shown below.
Workshop 6: Simulation air blast explosion over the composite panel concrete-titanium foam
In this tutorial, an air blast explosion over the composite panel(Concrete+Titanium foam) is simulated. Two parts are needed for this modelling: one for concrete and one for titanium foam. In this simulation, Crushable foam model with volumetric hardening is used; you can find its equations in the Abaqus documentation. The yield surface for the crushable foam model with volumetric hardening has an elliptical dependency of the deviatoric stress on the pressure stress. It is predicted that the volumetric compacting plastic strain that the material experiences dictates how the yield surface evolves. There are three ways to define contact between the concrete part and the titanium part: Creating a cohesive surface as an interaction property, using cohesive elements between concrete and titanium foam, and the third one is using the tie constraint between them, which is the method used in this modelling. For the air blast, CONWEP is used. You can see more details and results in the video.
I hope you have got enough information about the foam Abaqus simulation; if you have any questions about this tutorial, contact us via online chat here on the left side of the page.
It would be helpful to see Abaqus Documentation to understand how it would be hard to start an Abaqus simulation without any Abaqus tutorial.
- Introduction and problem description
- Description of modeling steps
- Result and discussion
- Introduction and problem description
- Description of modeling steps
- Result and discussion
- Introduction and problem description
- Description of modeling steps
- Result and discussion
- Introduction and problem description
- Description of modeling steps
- Result and discussion
- Introduction and problem description
- Description of modeling steps
- Result and discussion
- Introduction and problem description
- Description of modeling steps
- Result and discussion
All the package includes Quality assurance of training packages. According to this guarantee, you will be given another package if you are not satisfied with the training, or your money is returned. Get more information in terms and conditions of the CAE Assistant.
All packages include lifelong support, 24/7 support, and updates will always be sent to you when the package is updated with a one-time purchase. Get more information in terms and conditions of the CAE Assistant.
Notice: If you have any question or problem you can contact us.
Ways to contact us: WhatsApp/Online Support/Support@CAEassistant.com/ contact form.
Projects: Need help with your project? You can get free consultation from us here.
- Online payment: with MasterCard, VisaCard and etc.
- Offline payment: In this payment method, you should pay via PayPal and send your payment receipt as an attached file in the offline payment form.
- via download link After purchase, a download link will be sent to you a zip file included training videos, documents and software files.
- Send us your machine ID
To access tutorial video run the .exe file on your personal pc and send the generated code to shop@caeassistat.com and wait for your personal code, which is usable only for that pc, up to 24 hours from CAE Assistant support.
Here you can see the purchase process of packages: Track Order
You must be logged in to post a review.





















Reviews
There are no reviews yet.