Mohr-coulomb usage in Abaqus

Mohr-Coulomb theory

A mathematical model called Mohr-Coulomb theory describes how brittle materials, like concrete or rubble piles, react to both shear stress and normal stress. This rule is followed by the majority of traditional engineering materials in at least some of their shear failure envelope. The hypothesis typically applies to materials whose compressive strength is significantly greater than their tensile strength. The shear strength of soils and rocks is defined by this theory in geotechnical engineering under various effective stresses. Mohr-coulomb Abaqus simulation is fully discussed in this tutorial package.

It is used in structural engineering to calculate the failure load and the angle of a displacement fracture in concrete and other comparable materials. The shear and normal stress ratios needed to fracture a material are calculated using Coulomb’s friction hypothesis.

You will discover four real-world applications of this theory in this package: Dynamic analysis of a tunnel in soil subjected to internal blast loading, examination of surface explosion damage to an underground box tube in ABAQUS, Internal explosion-related numerical simulation of the damage mechanics of a pipeline and, in the circumstances involving crashworthiness, a simulation of the Eulerian approach to soil impact analysis. You can read more detail about the Mohr-coulomb Abaqus examples below.

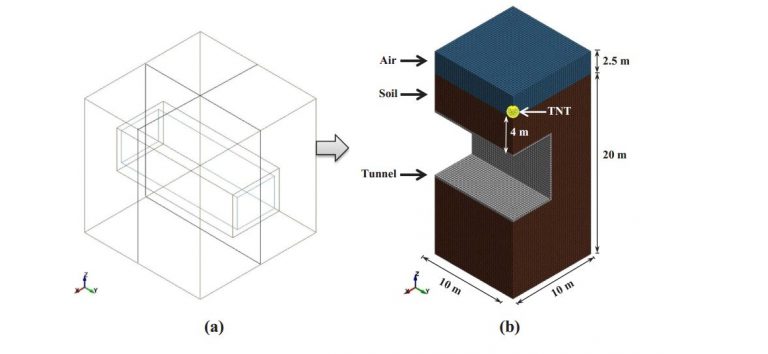
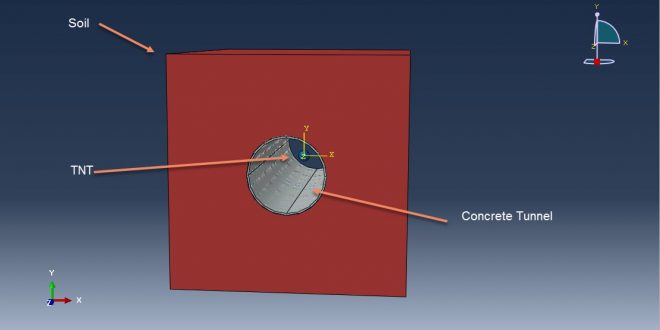
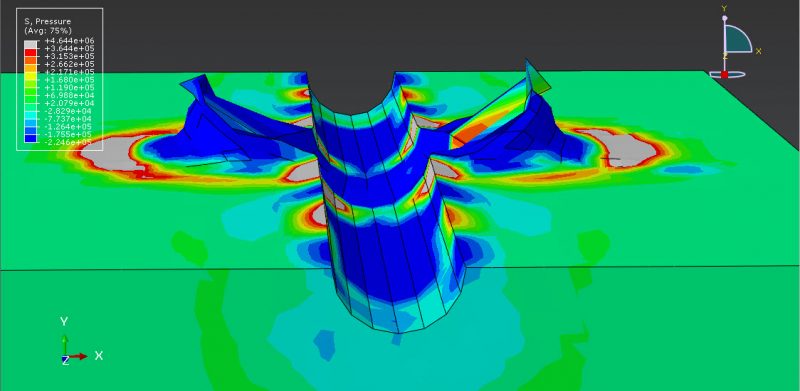
workshop 1: Damage assessment of an underground box tunnel by a surface explosion

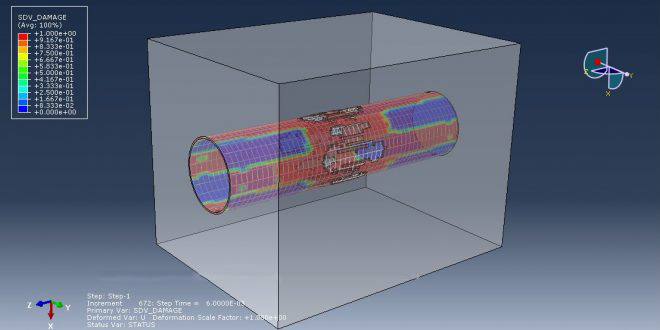
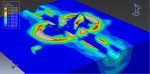
Because there are inadequate systems in place to detect external terrorist operations in time to take preventive action, they have recently become one of the occurrences that have the greatest impact on the safety of tunnel structures. The current simulation examined the behavior of an underground box frame tunnel brought on by a surface explosion using the ABAQUS program. TNT waves cause tension in the concrete tube during the explicit analysis as they travel through the air and the ground. Some simulation-related figures that you can see are presented in the above section.

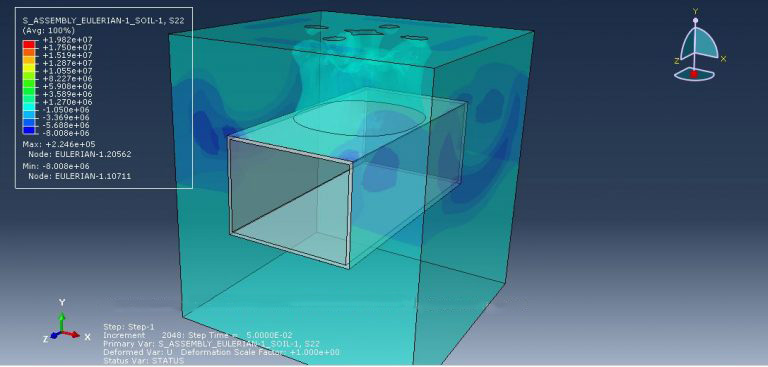
Workshop 2: Dynamic analysis of tunnel in soil subjected to internal blast loading by using the CEL method in Abaqus

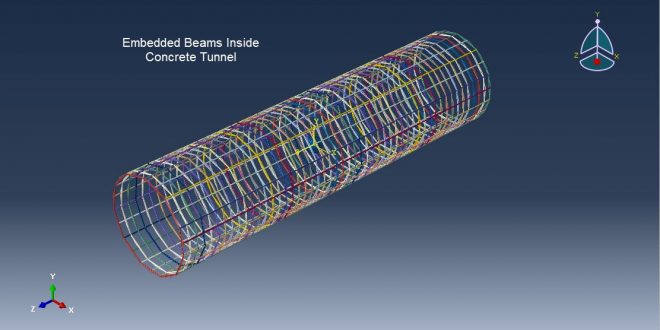
In this Mohr-coulomb Abaqus tutorial, the CEL method in Abaqus has been used to study the dynamic analysis of a tunnel in soil subjected to internal blast loading. In the model, the concrete tube is represented as a solid part, the domain as an Eulerian part, the TNT and dirt as solid parts, and the beam as a wire part. You can see some figures of the assembled parts below.

Tunnels for utility lines, water pipelines, underground roads and railroads are all essential components of the civil infrastructure. Explosion occurrences brought on by terrorist activity inside subsurface infrastructure have emerged as a significant menace to human civilization in recent decades. Due to the shock wave’s channeling caused by the blast-induced shock wave’s many reflections on the tunnel wall, internal explosions in tunnels are frequently more dangerous than explosions above ground. Therefore, it is essential to construct tunnels appropriately to withstand blast loading in order to protect them from explosive events. To do this, it is required to understand the tunnel’s response to blast loading experimentally and statistically. The focus of the current research is on the sophisticated numerical analysis of tunnels subjected to blast loads.

For the soil’s elastic properties and Mohr-Coulomb plasticity, for TNT’s JWL equation of state, and concrete tunnels because of their high pressure and susceptibility to collapse, the Johnson-Holmquist model is utilized. This kind of analysis is ideal for dynamic explicit method. All contact domains and embedding regions for beams inside concrete hosts have been taken into consideration. To specify the position and quantity of TNT, the Eulerian model volume fraction approach is employed. The Eulerian domain and the concrete tunnel are given the appropriate boundary conditions. Mesh has a positive impact on results, hence modest mesh sizes are required.

All results, including concrete damage variables, stress, damage to beams, strain, and other results, are available after simulation. (Mohr-coulomb Abaqus simulation examples)

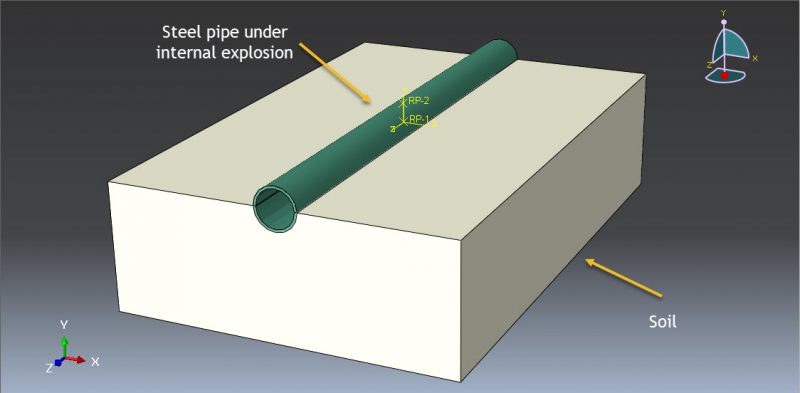
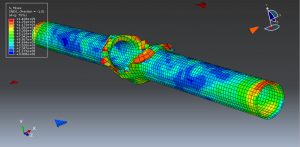
Workshop 3: Numerical simulation on damage mechanics behavior of a pipeline under internal explosion

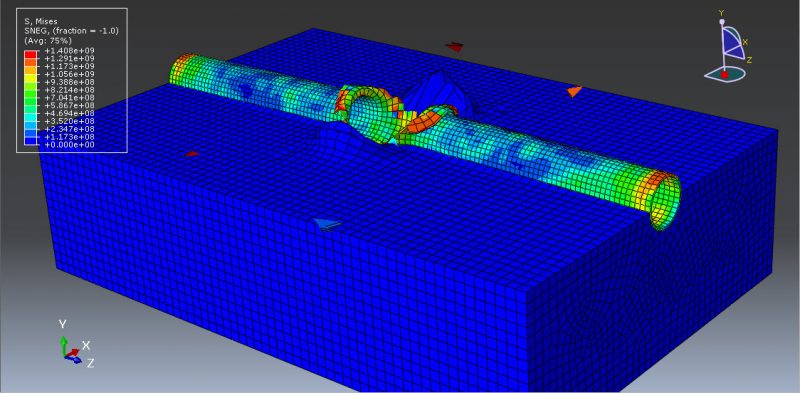
This tutorial looks at the damage mechanics behavior of an internal explosion on a pipeline using numerical simulation and Abaqus. A three-dimensional shell portion is used to simulate the steel pipe. The dirt is depicted as a solid part with three dimensions. The soil is inserted into the steel pipe on one side. The assembled parts are depicted in the figure below.

The pipeline offers features including a wide distribution range, a large tube pressure, and a long conveying distance. It is quite simple to cause explosion and combustion once a tube bursts and other catastrophes happen, leading to unfathomable loss of life and property. The variable medium conditions and intricate boundary conditions make it impossible to accurately answer the high-pressure pipeline blasting problem. For the steel pipe, the Johnson-Cook plasticity model is chosen. With analytical versions of the hardening law and, it is a specific kind of Mises plasticity model. Appropriate for high-strain-rate deformation of numerous materials, including most metals, rate dependence For the steel pipe, the JC plasticity and damage model is employed to account for high rate loads as well as damage from blast loads. For the soil component, the Mohr-Coulomb plasticity model is chosen. This kind of analysis is suitable for the dynamic explicit step. Friction is used as the primary form of contact behavior in general. The optimum contact or tie constraints are chosen to specify the contact between the lower surface of the steel pipe and the earth. Utilizing the TNT definition as the incident wave, the CONWEP blast technique is used. The soil’s subsurface is given the fixed boundary condition, while the pipe’s two ends are given the pin boundary condition. To get the right results, the mesh must be located.

The results are available after the simulation, including stress, strain, damage, swelling, soil deformation, blast depth, and more. You can see some Mohr-coulomb Abaqus figures for the results above.

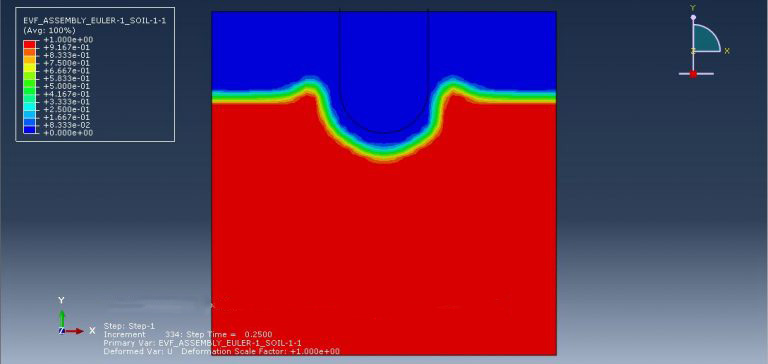
Workshop 4: Simulation of an eulerian approach to soil impact analysis for crashworthiness applications

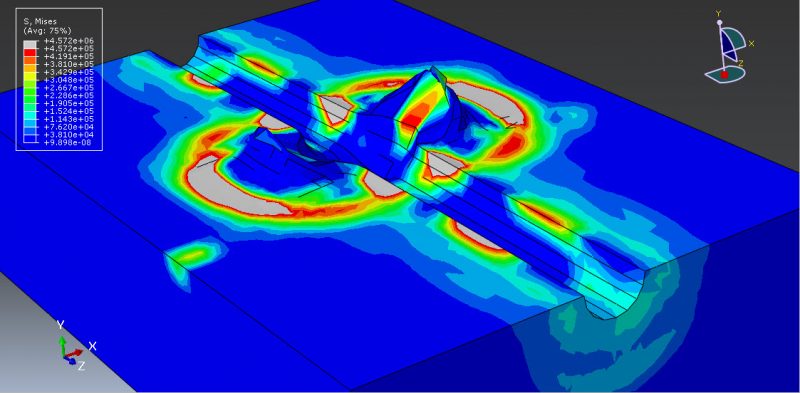
The invention and application of an explicit nonlinear dynamic finite element methodology for examining the crashworthiness of small, light-weight stiff impacts into soft ground served as the main driving force behind this study. The characteristics of the impact topography have a significant impact on how an airplane crashes since different terrains have a distinct structural impact. This work focuses on a method for characterizing and validating a numerical model for soft soil as an impact terrain. The technique was proven by the FEA of penetrometer drop experiments into soft soil. It was principally based on the usage of a time-explicit Eulerian-based FE analysis code. To reduce the numerical instabilities that frequently arise with the use of Lagrangian solvers when considering problems with large deformations, which is a characteristic of crash analyses, the Eulerian-based FE approach was taken into consideration than the more widely used Lagrangian-based FE approach. These numerical instability issues could end analyses early and taint the outcomes. Nonlinear transient dynamic investigations have made substantial use of explicit FE codes. In this simulation, the soil was modeled as an Eulerian component and the projectile as a rigid body. A projectile is inserted into the ground during the analysis, and a hole is made in the ground. Above are some simulation-related figures that you can see. I hope you have got enough information about the Mohr-coulomb Abaqus simulation; if you have any questions about this tutorial, contact us via online chat here on the left side of the page.

It would be helpful to see Abaqus Documentation to understand how it would be hard to start an Abaqus simulation without any Abaqus tutorial.