Introduction
This project features a comprehensive set of Abaqus models for 3D continuum elements, using a custom VUMAT subroutine. The model is based on the Modified Johnson Cook (MJC) thermo-viscoplastic model combined with the Hershey yield surface. If you work with high-strain-rate applications such as impact analysis, metal forming, or crash simulations, this modeling package will enhance your workflow.
What is the Modified Johnson Cook (MJC) Viscoplastic Model?
The Modified Johnson Cook (MJC) model is a material behavior framework designed to simulate how materials respond to different strain rates and temperatures. It’s an enhanced version of the classic Johnson Cook model, which was developed to predict the behavior of metals under extreme conditions like impacts or explosions.
The MJC model can take into account:
- Work hardening (how a material becomes stronger as it’s deformed)
- Thermal softening (how a material weakens at elevated temperatures.)
- Strain rate sensitivity (how material behavior changes with different speeds of loading)
In this implementation, the thermal softening is assumed to be due to adiabatic heating due to the plastic work being converted into heat. This is appropriate for short duration, high strain-rate scenarios, where heat conduction can be considered negligible.
By using the MJC model, simulations can more accurately reflect real-world conditions, making it ideal for industries like automotive and aerospace, where materials often experience both high temperatures and high strain rates.
What is the Hershey Yield Surface?
The Hershey yield surface is an advanced model for predicting when a material will begin to deform plastically under stress.
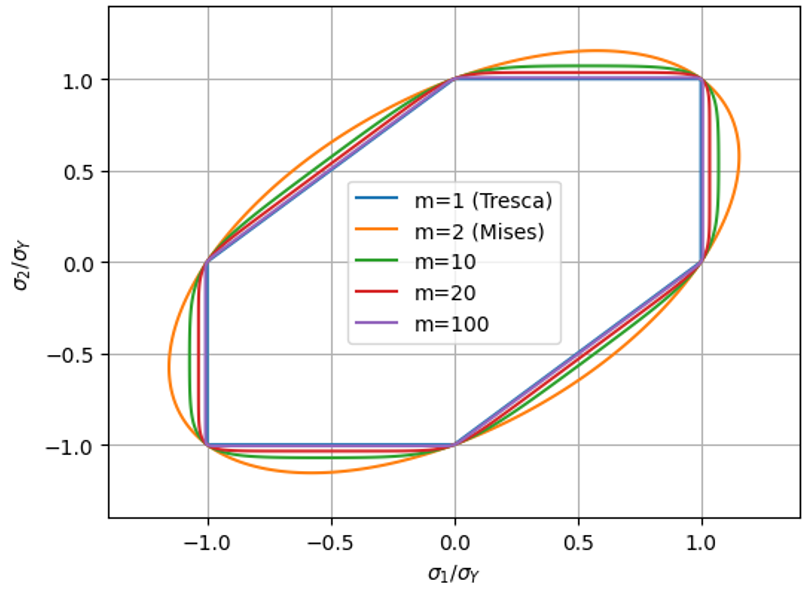
The Hershey yield surface can be viewed as a hybrid between the von Mises and the Tresca yield surfaces. The figure shows the form of the yield surface for different values of the exponent m. For the value m = 1, the criterion becomes Tresca and for a value of 2, the von Mises criterion is obtained. Other values of m gives a hybrid of the two.
Typically, real metals will have a yield surface that is somewhere in between the Tresca and von Mises yield surfaces. This behaviour can be described by the Hershey yield surface by setting an appropriate value of the exponent m.
This implementation assumes isotropic work hardening, meaning that the yield surface will be able to grow as it deforms plastically, but it will grow independent of the direction of the applied load.
Why Use the MJC Model and Hershey Yield Surface Together?
Using both the Modified Johnson Cook (MJC) model and the Hershey yield surface gives you a more precise simulation of material behavior under extreme conditions. The MJC model accounts for changes in temperature due to plastic dissipation as well as plastic strain rate, while the Hershey yield surface realistically describes the yielding behavior of metals. Together, they enable simulations that closely replicate the performance of real-world materials, even under extreme conditions.
This combination becomes especially important in applications where high-speed impacts, high temperatures, or both affect materials—such as in crash tests, ballistic impact studies, and advanced manufacturing processes like hot metal forming.
How are the Equations Solved?
Every time step, the VUMAT subroutine is responsible for updating the stress and internal variables describing effects such as work hardening, temperature, etc. For every integration point in every element of the mesh, a set of nonlinear equations governing the material model have to be solved. To solve these equations, a return mapping algorithm is used. First an elastic predictor step is performed which gives a predicted stress state. If this stress is outside the yield surface, a plastic corrector step is performed. This corrector step is solved by an iterative scheme. The selected scheme in this implementation is a robust algorithm called the cutting plane method, suitable for explicit codes.













Reviews
Clear filtersThere are no reviews yet.