1. Introduction: Abaqus implementation of the Maxwell viscoelastic model
The behavior of viscoelastic materials is a state between the behavior of a liquid and a solid. In other words, they behave both like liquids and solids. That is to say, many natural and synthetic materials are classified as viscoelastic materials; From the biological structures of the body such as skin, cartilage, and tissue to concrete, foams, rubbers, and synthetic polymers. Due to these unique properties, viscoelastic materials have many applications. In this regard, the primary goals of this study include the development and implementation of an accurate three-dimensional model of viscoelastic materials, and the integration of viscoelastic properties into the analysis, which can improve the prediction of viscoelastic materials response under different boundary and loading conditions.
This project uses the UMAT subroutine to simulate the behavior of viscoelastic materials with the generalized rheological Maxwell viscoelastic model. The geometric model used in this study is a specimen under tension. The behavior of viscoelastic materials is a state between the behavior of a liquid and a solid. In other words, they behave both like liquids and solids. There are many natural and synthetic materials that are classified as viscoelastic materials; From the biological structures of the body such as skin, cartilage, and tissue to concrete, foams, rubbers, and synthetic polymers. Due to these unique properties, viscoelastic materials have many applications.
In this regard, the primary goals of this study include the development and implementation of an accurate three-dimensional model of viscoelastic materials, and the integration of viscoelastic properties into the analysis, which can improve the prediction of viscoelastic materials response under different boundary and loading conditions.
In this tutorial, the generalized Maxwell viscoelastic model is discussed, and after explaining the theory and mentioning the details of this model, the related subroutine is presented.
2. Simulation of the Generalized Maxwell model of viscoelasticity using UMAT Subroutine (PDF File)
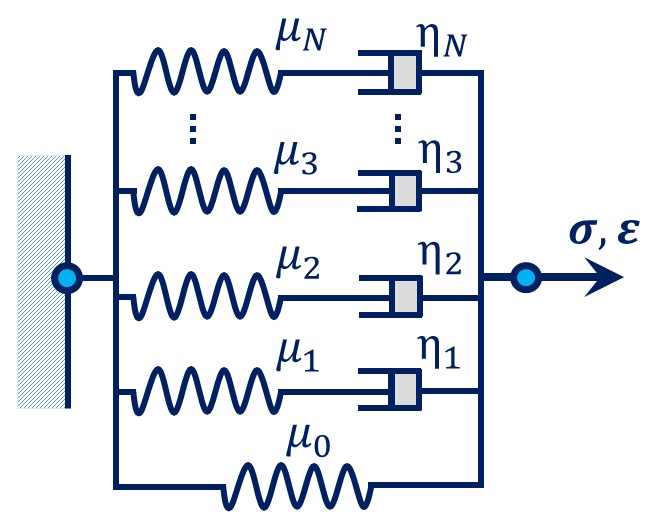
This project, after teaching the basic fundamentals of material rheological modeling, presents a precise three-dimensional mechanical response of viscoelastic materials using a generalized Maxwell viscoelastic model. That is to say, the implementation of the Maxwell model of viscoelasticity is done with the UMAT subroutine (for standard solver).
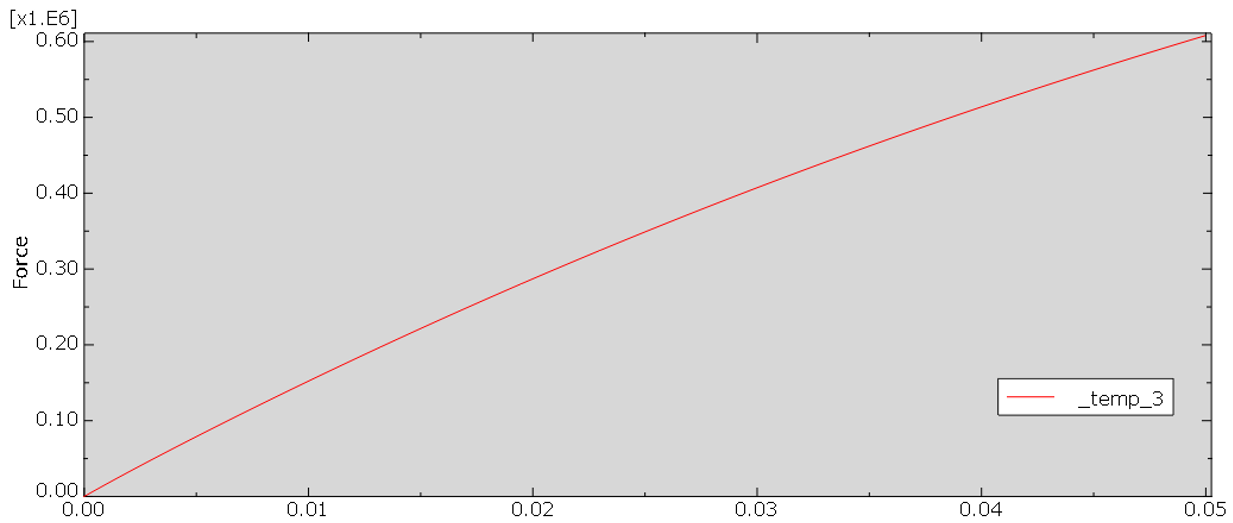
2.1. Problem Description
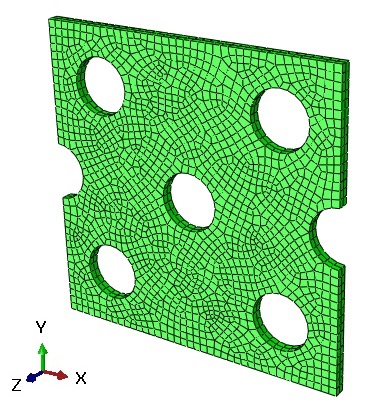
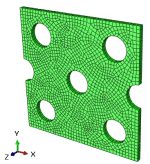
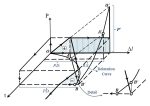
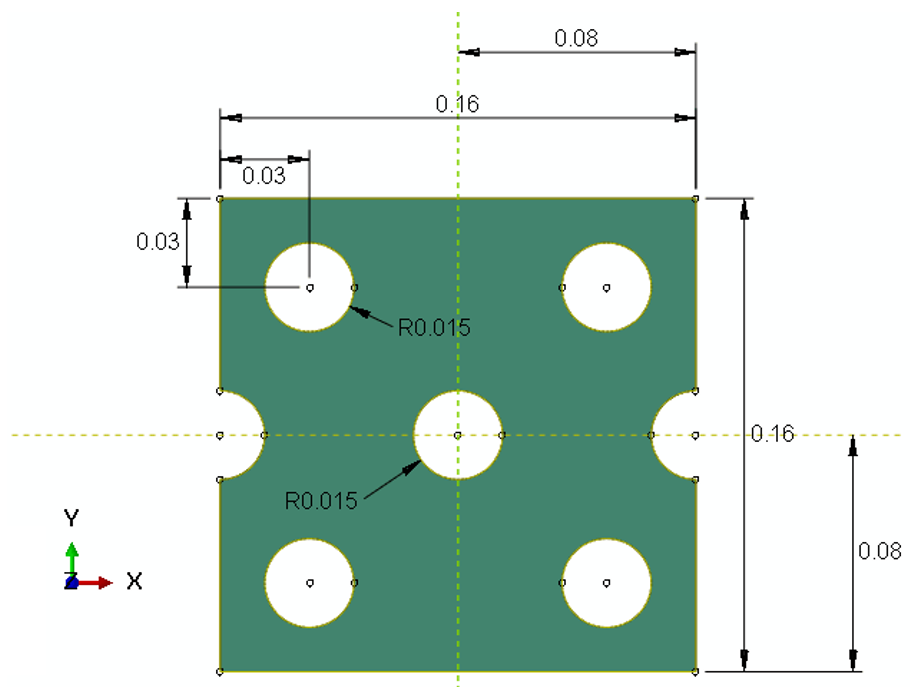
Geometry: This example includes a Lagrangian part subjected to tension. We show the schematic design of the part in Figure 1.
We present the material properties used in this example in an Excel file named ‘Material Properties’. These properties are imported into the UMAT subroutine. The materials used in this example are epoxy, VHB 4910, and VHB polymers.
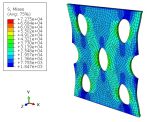
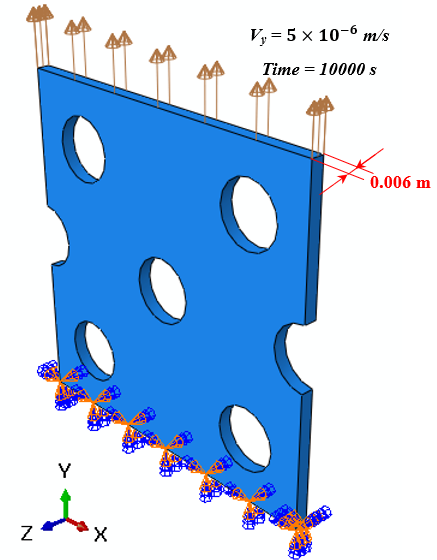
The upper surface of the part is pulled using the velocity boundary conditions and all degrees of freedom of the bottom surface are restrained, as illustrated in Figure 2.
Figure 1: The schematic design of the tensile part
Figure 2: The velocity boundary conditions
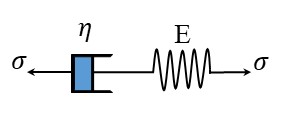
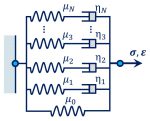
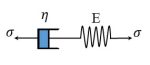
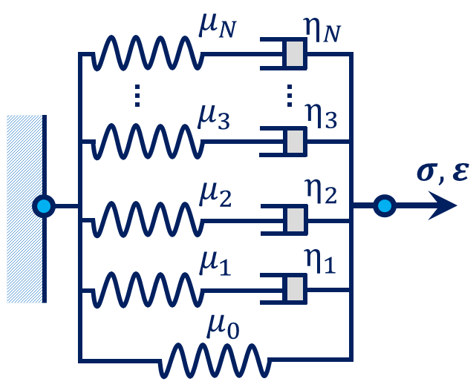
Figure 3: Schematics of the generalized Maxwell model
2.2. Project Procedures
- Setting up the software environment and choosing Abaqus units;
- Creating the tensile part;
- Defining the material properties and creating its relevant section;
- Making an instance of the model in the Assembly module;
- Creating a non-linear “Static, General” step for doing analysis by calling the UMAT subroutine;
- Determining the loading and boundary conditions, etc.;
- Generating elements and assigning element types;
- Preparing the “UMAT_5Maxwell_Elements” subroutine;
- Creating the jobs and calling the UMAT subroutines for the relevant jobs;
- Submitting the jobs;
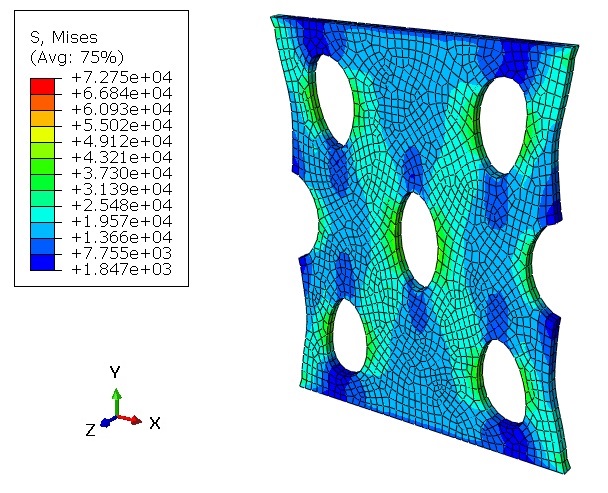
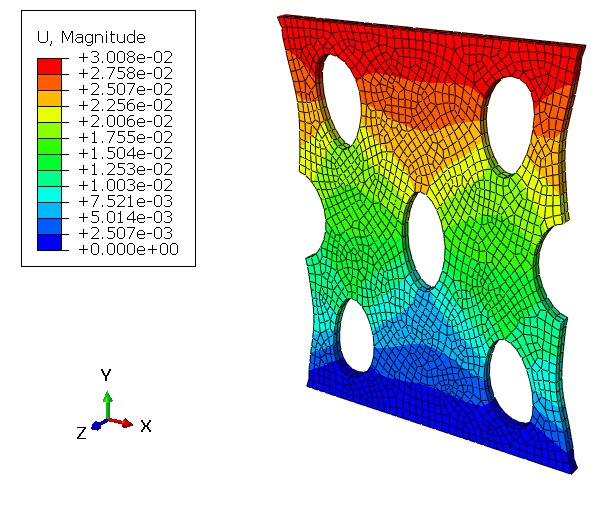
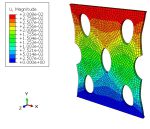
- Viewing the results.
m/s).
), reaction forces (RF), force-displacement diagram (F-U), stress-strain diagram (S-
Reviews
There are no reviews yet