Using Viscoelastic and Path-Dependent Models for Analyzing the Curing Process in Fiber-Reinforced Composites With Abaqus subroutines

Introduction

Fiber-reinforced composites are materials made up of at least two distinct parts: fibers and a matrix. The fibers serve as the main load-bearing element, while the matrix binds the fibers together, shields them from harm, and enhances the material’s overall structural cohesion. This synergy creates a composite with improved properties that outperform those of each component. Their exceptional properties make fiber-reinforced composites (FRCs) widely used in areas where a blend of strength, rigidity, and lightweight is crucial. For example, we can refer to aerospace, automotive, construction, sports equipment, and more. Achieving such high-performance applications demands high-quality manufacturing, heavily reliant on an optimized curing process. An improperly optimized curing process can introduce residual stresses or strains, compromising the final product’s quality. This underscores the importance of careful analysis and control of the curing process, a topic explored in this package.

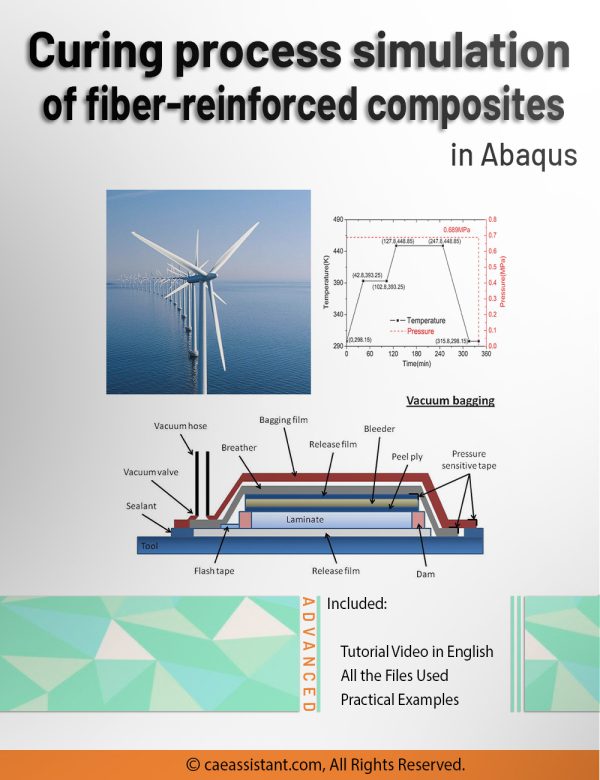
Composite manufacturing process

Manufacturers typically produce composites using two primary methods: Resin Transfer Molding (RTM) and Prepreg processing. In RTM, they inject resin into a mold containing dry reinforcing fibers under carefully controlled pressure and temperature conditions. In the Prepreg method, they pre-impregnate reinforcing fibers with a partially cured resin matrix. During manufacturing, these pre-impregnated sheets undergo additional heat and pressure to complete the curing process. Both techniques apply cycles of pressure and temperature to transform the resin from a liquid to a solid state. This process, known as curing, is a critical phase in production and requires a high level of precision.

Curing process in composites and its importance

The quality of curing in fiber-reinforced composites is heavily influenced by both time and temperature. High-quality composites typically require several hours of curing at an optimal temperature, which can slow down production and reduce efficiency. To improve production efficiency, manufacturers may reduce curing times by using higher temperatures. However, this approach can introduce residual stresses or deformations in the composite, potentially affecting its overall quality. To achieve a high-quality composite, it is essential to keep residual stress and deformation within acceptable limits while optimizing production efficiency. This requirement leads to the design of highly efficient curing cycles.

Designing the curing cycles for the production of composites

One approach to designing an optimized curing process is to perform multiple curing cycles on a specimen, using trial and error to balance quality and performance. However, this method is costly, time-consuming, and often lacks precision. To overcome these challenges, numerical methods for simulating the curing process have been introduced. They enable efficient and accurate design of curing cycles.

Using numerical methods to analyze the curing process in composites

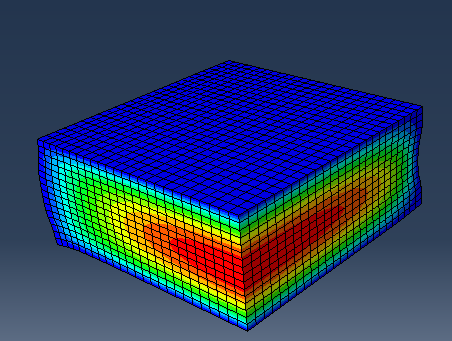
Various numerical methods have been introduced in the literature for analyzing curing in composite materials, many of which rely on the finite element method. This approach involves multiple fields, including thermal, chemical, and mechanical models. The thermal model predicts the heat distribution within the material during curing. Based on the results from the thermal model, the chemical model calculates the heat generated by thermal reactions as a function of the degree of cure. The resulting temperature increase can induce thermal strains in the material, while the chemical reactions generate chemical strains. These strains ultimately translate into stress within the composite, resulting in a complex chemical-thermal-mechanical interaction.

To predict residual stress or deformation in a composite resulting from the curing process, we require two sets of equations: thermo-chemical and thermo-mechanical. The thermo-chemical model, which is simpler to define and apply, calculates the degree of cure as a function of the chemical reactions triggered by temperature changes within the material. This topic is discussed in detail in this project.

Calculation of the residual stresses due to the curing process

When analyzing the curing process, calculating residual stresses is more complex than determining the degree of cure. This complexity arises because resin exhibits varying behaviors throughout the different stages of curing, which are influenced by temperature and the degree of cure. In the early stages, the resin behaves as a viscous material, unable to support significant stress. As curing progresses, it transitions into a viscoelastic state, exhibiting rubber-like characteristics. Eventually, both viscous and elastic behaviors combine. Then the resin reaches a fully elastic, solid-like state upon completion of the curing process. This progression complicates the analysis of the resin’s mechanical behavior and the resulting stresses within the composite during curing.

Existing models to analyze curing residual stresses in composites

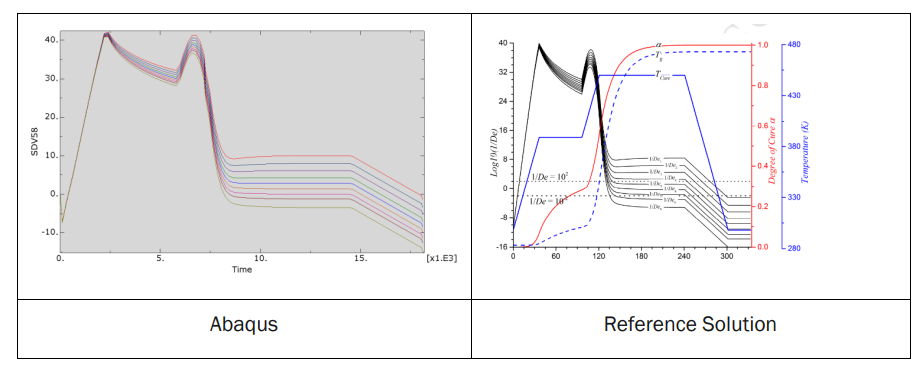
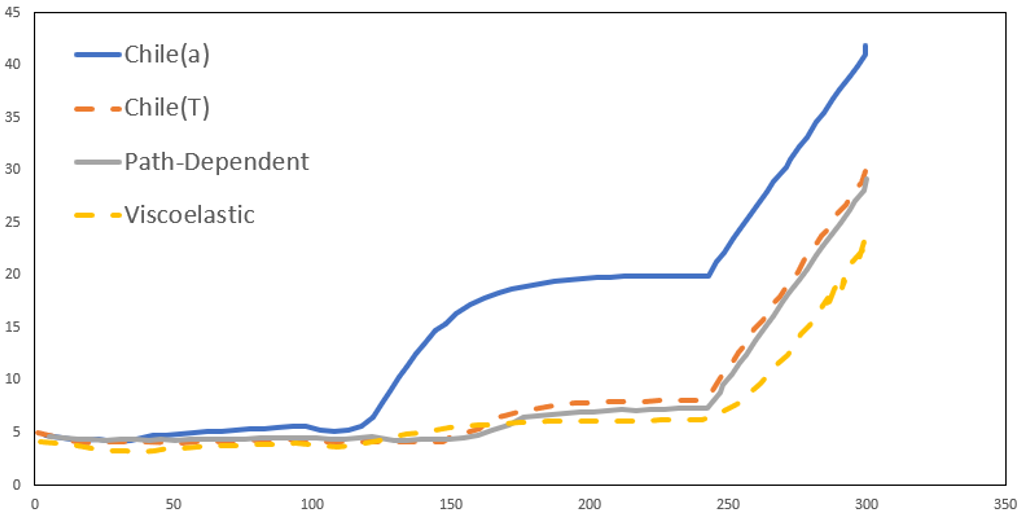
In the early literature, elastic models were developed to analyze residual stresses in composites during curing. They were known for their simplicity of use. They include the Chile(Alpha) and Chile(T) models. These models assume that the material remains elastic throughout each step of the curing process, while the resin’s elastic modulus is a function of the degree of cure or temperature. Chile(Alpha) and Chile(T) models are frequently used in the literature, as discussed in this training package, primarily for their simplicity. However, neglecting the viscoelastic behavior leads to overestimated residual stress predictions and unrealistic results.

Viscoelastic models

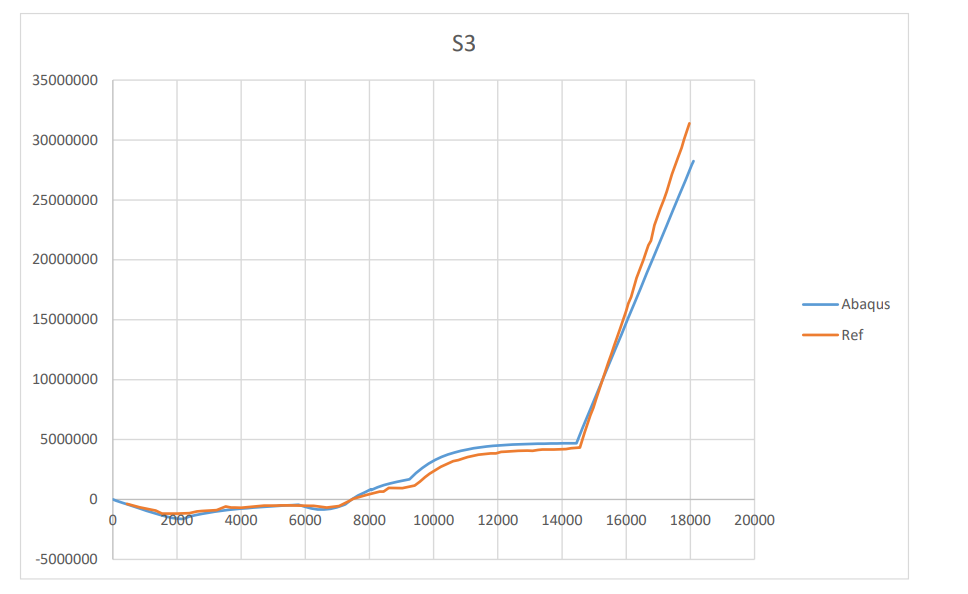
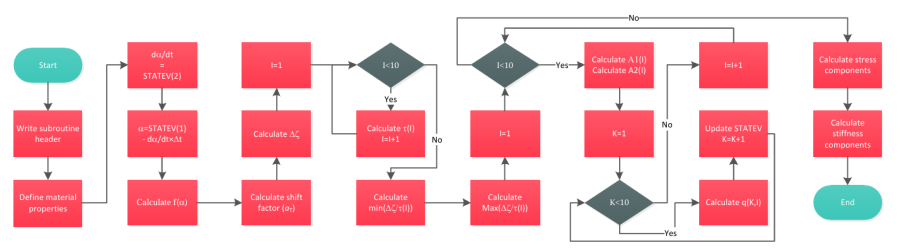
To improve the accuracy of residual stress predictions during curing, viscoelastic models have been developed. These models assume that the resin exhibits viscoelastic behavior. Consequently, they update the composite stiffness matrix at each incremental step in static solvers, based on the resin status. The generalized Maxwell model is used to define the stiffness matrix. This approach closely aligns with the material’s actual behavior, enabling a more accurate evaluation of residual stresses during the curing process. In this package, we have discussed the formulation and theory behind the viscoelastic model, and its discretization for the numerical models in detail. For the discretization, we have approximated the stiffness matrix with the Prony series.

Path dependent models

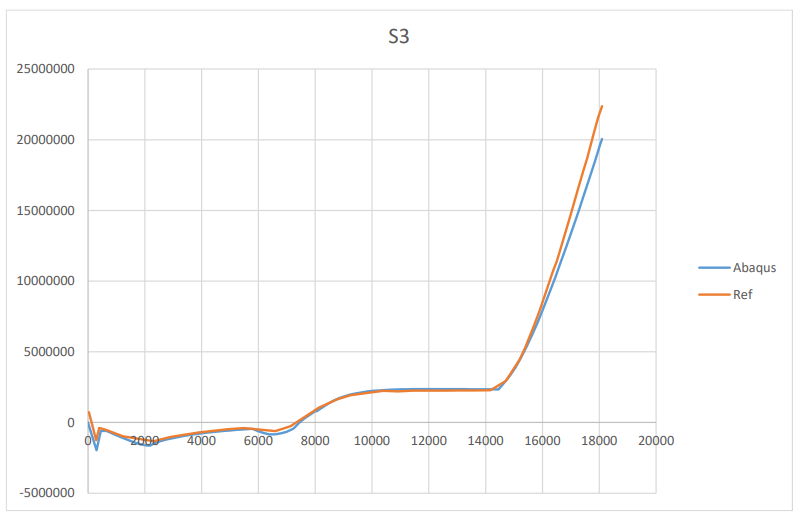
While the viscoelastic model provides accurate evaluations of residual stresses, it has one major drawback: its dependence on multiple factors that must be determined for each composite through extensive experimental testing. This requirement can make the viscoelastic model impractical, in some cases, despite its accuracy. Researchers developed path-dependent models as simplified versions of the viscoelastic model to address this issue, incorporating specific assumptions. They believe these models are more realistic than elastic models and closely approximate the accuracy of the viscoelastic model. So, they offer reliable predictions of residual stresses in composites during curing without the need for numerous experimentally determined factors and parameters. We have also discussed a well-known path-dependent model and its implementation in Abaqus software in this package.

Using Abaqus for the simulation of the curing process in composites

Abaqus is one of the most powerful and reliable tools for simulating curing in composites. To achieve this, you can use a set of its Fortran-based subroutines based on your desired parameters and models. For example, subroutines such as DISP, HETVAL, USDFLD, UEXPAN, and UMAT can be utilized. DISP applies curing temperatures, HETVAL calculates the internal heat generated during the curing process due to chemical reactions, UEXPAN calculates and assigns non-mechanical strains, including thermal and chemical, and finally, UMAT defines the material’s mechanical behavior. In one of our packages, we used these subroutines to simulate curing behavior using the Chile(Alpha) and Chile(T) models. However, in the current package, we aim to present a more advanced topic: the implementation of viscoelastic and path-dependent models in Abaqus subroutines to simulate the residual stresses generated during the curing process of composites. Using such models, the results are more realistic compared to those of the linear elastic ones in our intermediate package.