Implementation of Soil Constitutive Models in Abaqus | With a Special Focus on CSJ Models

Introduction

In the field of geotechnical engineering there are numerous Constitutive models. Among them, elastoplastic constitutive models serve as appropriate mathematical representations that describe the complex behavior of soils under various loading conditions. These models incorporate both elastic (reversible) and plastic (irreversible) deformations. They are essential for accurately predicting soil response in geotechnical engineering applications. For example, we can refer to foundation design, slope stability analysis, and earthquake engineering. By capturing the nonlinear behavior of soils, these models provide a more realistic representation of their mechanical properties. This leads to improved design decisions and enhanced safety.

The CJS model

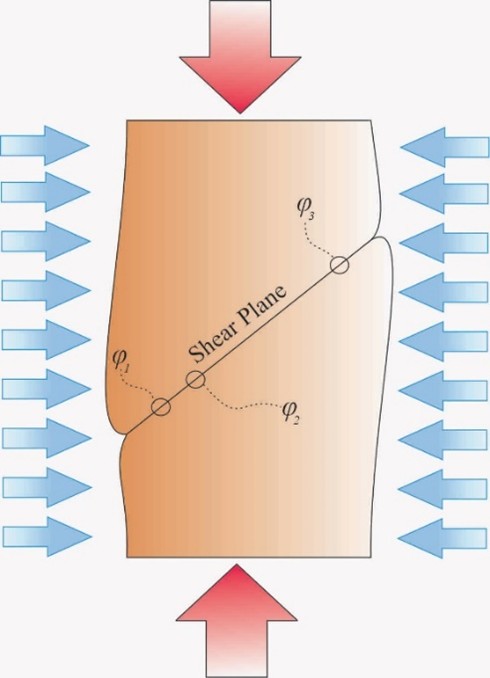
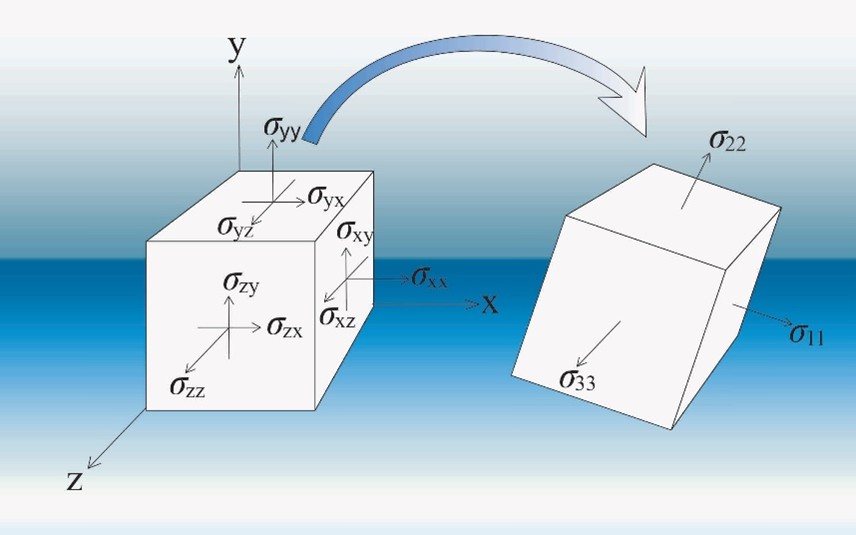
Researchers widely employ the CJS model as a relatively simple elasto-plastic constitutive model. In addition to the elastic component, it includes two plastic mechanisms: one isotropic and the other deviatoric. The isotropic mechanism’s yield surface is a plane that is perpendicular to the hydrostatic axis in stress space, with its evolution dictated by an isotropic hardening rule. For the deviatoric mechanism, the yield surface follows a non-associated flow rule. It is governed by a combination of isotropic and kinematic hardening laws. In the simplified CJS model, the deviatoric mechanism uses purely kinematic hardening.

Abaqus implementation of the CJS model

Abaqus, with its subroutines, is one of the most powerful software tools that simplifies the implementation of CJS models. This is a challenging aspect, that needs an advanced knowledge of the implementation of isotropic and kinemetic hardening models in Abaqus subroutines. The matter is discussed in this project. This project will help you learn to implement a constitutive model in Abaqus by focusing on model CJS.

What you will learn from this tutorial

In this tutorial, we will try to provide guidance for the installation and operation of these models by presenting the content in the following 6 sections.

1. How do constitutive models work with a complete description of two classical models, Cam-Clay and Mohr-Coulomb models.
2. Types of hardening and their application with numerical examples (Isotropic, Kinematic and Mixed hardening)
3. Description of the coding of constitutive models in ABAQUS with the ABAQUS manual example for Von Mises model (in VUMAT).
4. State the difference between VUMAT and UMAT and describe a written model in UMAT code.
5. Description of the CJS model and how to use it.
6. Describing CJS-II and CJS-III coding and solving examples with them.

Finally, users should be able to understand the advantages and disadvantages of different models and install a new model in Abaqus if needed.

The Importance of Nonlinear Soil Behavior Analysis

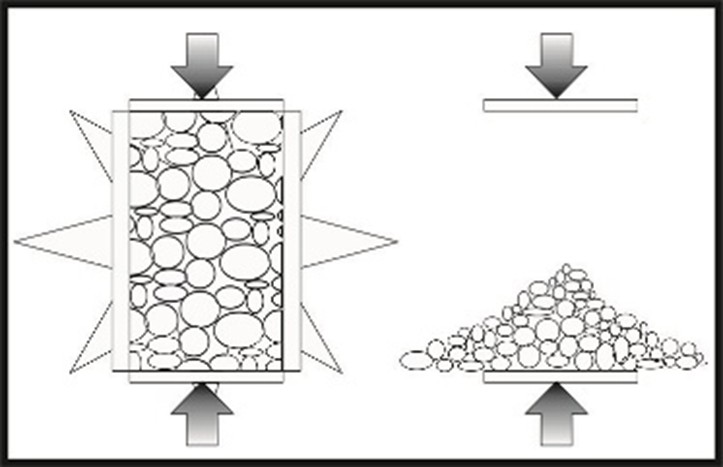
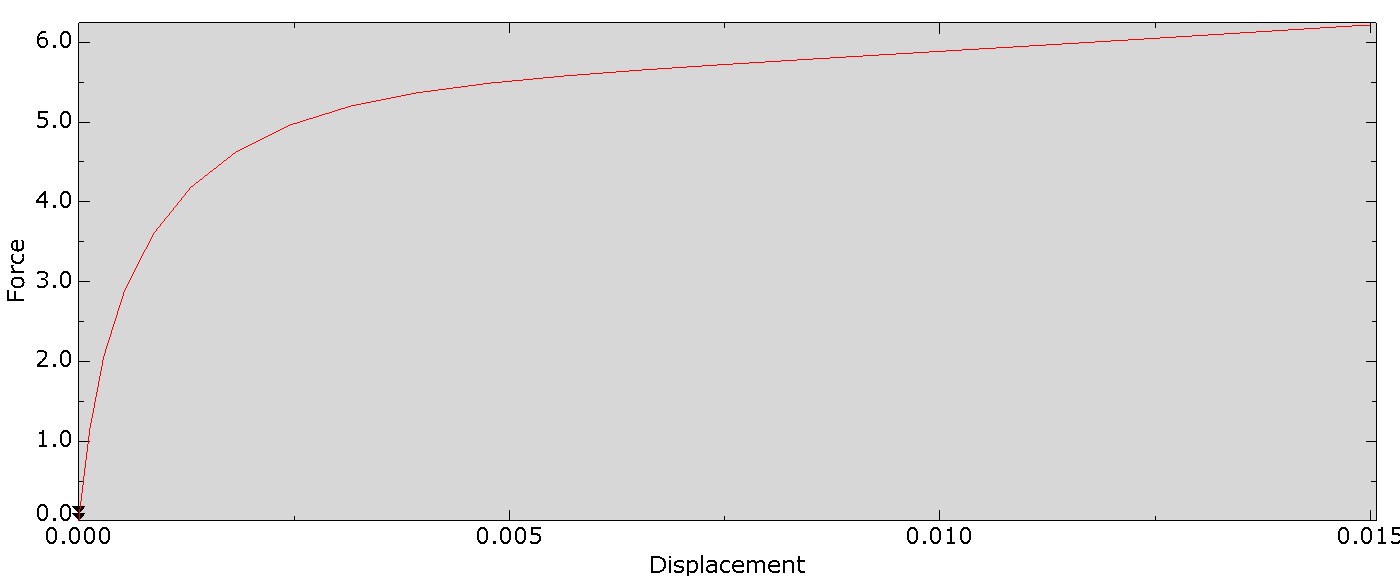
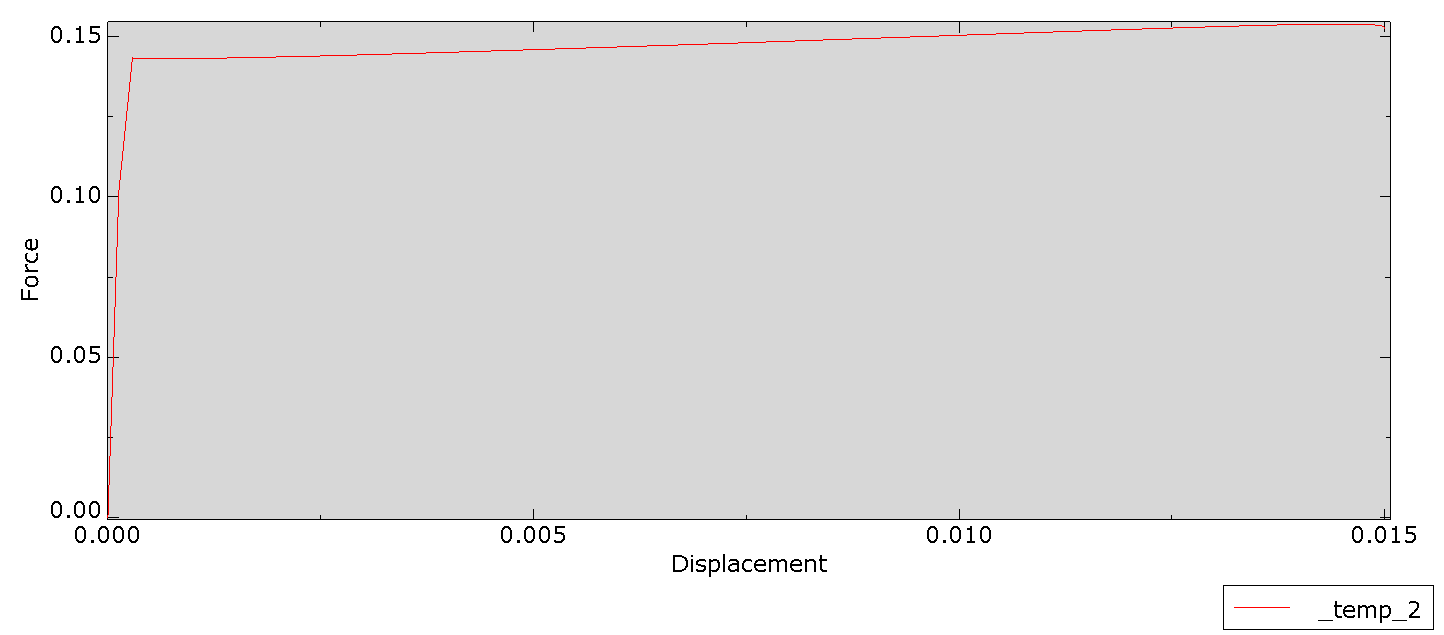
Analyzing the nonlinear behavior of soil is crucial for understanding how soils respond under various loading conditions. It is particularly important in engineering applications like foundations, retaining structures, and embankments. Soils exhibit complex behaviors, including plastic deformation and strain hardening, which must be accounted for using advanced soil constitutive models. Hardening constitutive models, such as isotropic and kinematic hardening, allow for more accurate predictions of soil behavior. They enable us to capture how soil stiffness evolves with increasing load and deformation. This is essential in applications involving large-scale infrastructure, where safety and stability depend on accurately modeling soil’s capacity to undergo significant stress and strain without failure. Moreover, nonlinear analysis ensures that engineers can predict settlements, cyclic loading effects, and post-yield behaviors, making it a vital part of geotechnical design and risk assessment.

Constitutive modeling of soils and rocks

Constitutive modeling of soils and rocks can be conducted using numerical methods. Alternatively, we can use experimental methods to predict soil behavior. We will discuss both approaches in the following sections.

Experimental methods

Experimental methods, such as triaxial, shear, and oedometer tests, provide direct insights into soil responses under controlled conditions, allowing researchers to observe behaviors like elasticity, plasticity, and strain hardening in real time. The main benefit of experimental methods is their accuracy and ability to capture real-world soil behavior, but they can be time-consuming, costly, and sometimes difficult to replicate for complex loading conditions.

Numerical methods

Numerical methods, such as the finite element method (FEM) or finite difference method (FDM), use mathematical models and simulations to predict soil behavior under various scenarios. These methods are highly flexible, allowing for complex analyses under diverse conditions, and are less expensive than experimental testing. However, the accuracy depends on the quality of the constitutive models used and the assumptions made during modeling. While numerical methods offer greater efficiency, researchers must validate their results against experimental data to ensure reliability.

Using Abaqus for the Implementation of Different Types of Soil Models

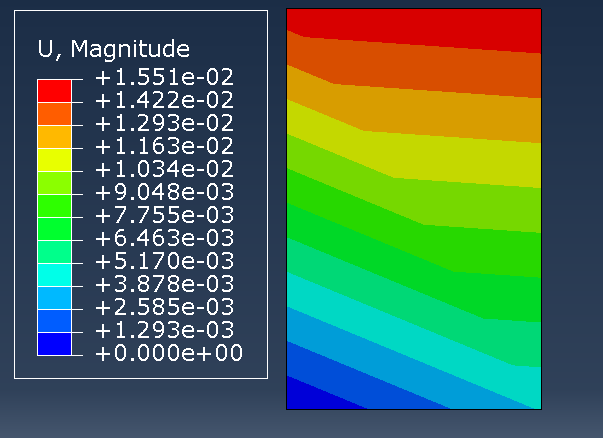
Abaqus is widely used for simulating different types of soil models due to its robust finite element capabilities and the ability to incorporate complex soil constitutive models. It allows for the accurate modeling of both linear and nonlinear soil responses under various loading conditions, including static, dynamic, and cyclic loads. Abaqus supports the implementation of advanced material models, such as elasto-plastic, viscoelastic, and creep models, making it ideal for capturing the characteristics of soils.

Using Abaqus Subroutines for the Simulation of Soil Behavior

One of the main advantages of Abaqus is its capability to handle large deformation problems and simulate soil-structure interactions, which is crucial for applications such as foundation design, embankments, and retaining walls. However, despite its flexibility, achieving accurate simulations in Abaqus requires careful selection of material parameters and a well-defined model, necessitating significant expertise in soil mechanics and numerical modeling. Additionally, the built-in Abaqus material model library is limited to specific models, which may not always be suitable for all materials. To overcome this limitation, user-defined subroutines, such as UMAT and VUMAT, allow for further customization of constitutive models, enabling researchers to implement specific soil constitutive models, like the CJS model.

Using Abaqus in this tutorial

In this tutorial, we aim to provide you with all the knowledge needed to implement nonlinear models in UMAT and VUMAT subroutines, with a focus on the CJS model for soil.