Lesson 1 & 2: Introduction to wood damage FEM
Wood is a natural material that provides structural support for trees and other plants. It has a wide range of applications, such as in construction, furniture making, and paper production. Despite its many applications, wood can suffer damage that may limit its uses. Insufficient strength in a wooden structure can lead to total failure, resulting in irreversible human and financial losses.
Early detection of damage is crucial for repairing and restoring sufficient stiffness in existing wooden structures. This also ensures the reliability of new structures. However, experimental methods for predicting wood damage require specific testing tools, which can be costly and challenging to use. To address these difficulties, numerical simulations using wood damage FEM offer a more cost-effective and less destructive alternative. We can adapt these simulations to a wide range of conditions and materials. Moreover, they are considered safe since they do not pose potential risks to humans. They also allow for comprehensive analysis of wood behavior, making them time-efficient and valuable.
Is numerical simulation of wood damage challenging?
Despite the benefits of numerical simulations compared to experimental methods, there are several issues and complexities associated with using such methods for predicting damage in wood structures. We will discuss these in detail in the following.
The accuracy of numerical models heavily depends on the input data. So, careful specification of the problem’s properties is essential to ensure accuracy. Moreover, wood exhibits complex behavior, showing different strengths in compression and tension. This complexity means that not all existing damage models are applicable to wood. On the other hand, wood demonstrates both brittle and ductile behaviors simultaneously, requiring advanced models that can accommodate both types of behavior.
Regarding the limitations related to continuum mechanics, models with softening can suffer from mesh dependency problems, which may lead to physically inadmissible solutions. Moreover, numerical models require different input parameters such as stiffness and strength values, which are typically derived from tests. Obtaining these parameters can be challenging due to the inherent variability in the mechanical properties of wood and the difficulties associated with testing and measurement.
All these factors make using numerical simulations challenging and require careful consideration and expertise to ensure reliable predictions. Consequently, we have limited numerical models that can accurately capture wood damage FEM.
Lesson 3: Numerical methods for damage prediction in wooden structures
We have three well-known numerical models for predicting wood damage, in literature, as:
- The Hashin model
- The Sandhaas model
- The Balsa model
These models are recognized for their accuracy in predicting whether a failure has occurred at a material point. Additionally, we can extend them to evaluate damage propagation and stiffness reduction in wood due to failure. These capabilities make them integral to wood damage FEM. We review them in more detail in the following sections.
The Sandhaas model
The Sandhaas model is a well-known numerical model primarily used to predict failure initiation and propagation in wood. It is primarily developed to predict whether a failure has occurred at a material point. To do so, it requires material strength parameters as input data to check for failure. For example, this includes tensile and compressive strengths parallel and perpendicular to the grain.
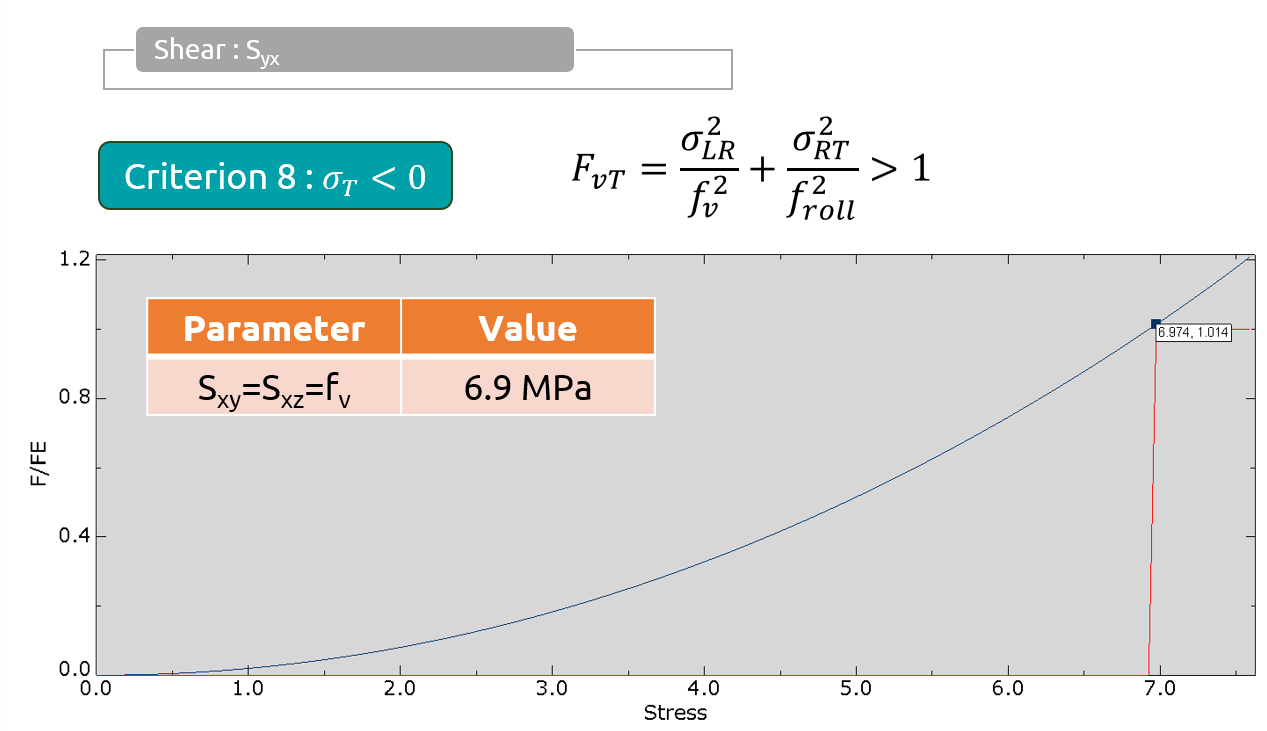
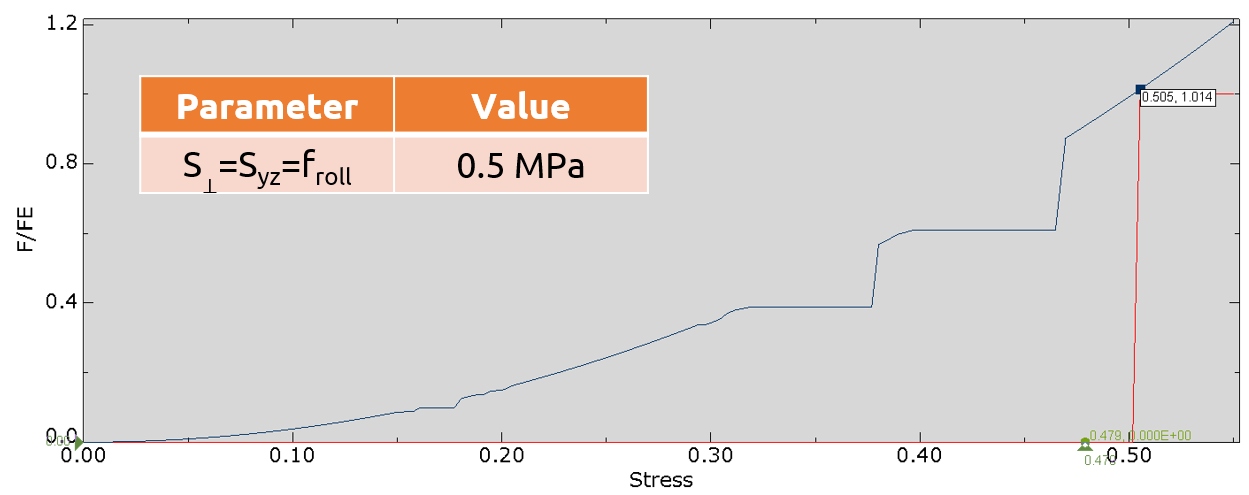
The Sandhaas model considers 8 failure states to determine whether the wood has failed. Failure occurs when a combination of stress components exceeds the material’s strength. Moreover, the model is often used in conjunction with a Continuum Damage Mechanics (CDM) model to assign damage to the failed material and degrade its stiffness, thereby capturing the real behavior of a failed material. The damage model frequently used with the Sandhaas criterion is a nonlinear elastic model that introduces nonlinearity by modifying the stiffness matrix during the solution. However, the model is simplified by neglecting plastic deformations during unloading.
In conclusion, the Sandhaas model is popular among researchers and practitioners for its useful features and is often used to predict failure initiation without considering damage and stiffness reduction due to the propagation of failure. Many practitioners combine it with a CDM model to capture stiffness degradation and damage propagation in the material.
The Hashin model
Hashin is another numerical model we use to predict failure in wood. The Hashin model defines failure modes with two main rules:
- Transversely Isotropic Behavior: The model considers the wood as transversely isotropic, meaning its properties are the same in both directions perpendicular to the grain.
- Shear Stress Effects: Shear stress can reduce wood’s resistance to compression or tension.
Based on these rules, the model considers four modes of failure. A value of 1 indicates that failure has occurred, while 0 indicates that the point has not failed. We can also extend the model to reduce stiffness parameters and predict damage propagation in the material.
The Balsa model
The Balsa model refers to a specific numerical model used to predict damage in Balsa wood. Balsa wood has many industrial applications, including thermal insulation for refrigerated ships, flotation aids in lifeboats, lightweight core material for sandwich panels, and packaging applications.
The model assumes that wood is transversely isotropic, meaning its properties are the same in both directions perpendicular to the grain. Moreover, it uses a simple failure criterion, compared to the Hashin and Sandhaas models. In this model, failure occurs when the equivalent stress exceeds the equivalent yield strength. Accordingly, we must calculate the equivalent stress using a specific equation that involves the stress components related to different axes.
Lesson 4: Implementation of the wood damage Abaqus
Abaqus is a powerful tool that plays a crucial role in predicting damage in wooden structures. It provides a platform for implementing advanced numerical models. The software supports numerical simulations, which are cost-effective and less destructive methods for damage prediction compared to experimental techniques. These simulations can predict whether a failure has occurred at a material point and evaluate damage propagation and stiffness reduction. Additionally, Abaqus offers tools to handle the complex behavior of wood, including its varying strengths in compression and tension, as well as its simultaneous brittle and ductile behaviors. This capability allows for the use of advanced models that accommodate these behaviors, making wood damage Abaqus simulations highly effective.
To perform such simulations, the VUSDFLD subroutine in Abaqus can be used. This subroutine allows for the definition of field and state variables, which can then be incorporated into the Abaqus simulation. Â Note that VUSDFLD is designed for use with explicit steps in Abaqus. For general static steps, we can use the USDFLD subroutine instead.
Using the VUSDFLD subroutine to predict wood damage Abaqus
Abaqus allows the use of the VUSDFLD subroutine, which enables users to define field variables as functions of time or other material point quantities. This subroutine helps define solution-dependent material properties and uses state variables during the solution process to develop a model. By implementing the VUSDFLD subroutine, Abaqus facilitates the incorporation of well-known failure models such as the Hashin, Sandhaas, and Balsa. This capability is particularly useful for implementing complex wood damage FEM models that require custom material behavior definitions.
By leveraging these capabilities, Abaqus helps overcome the challenges associated with numerical methods for predicting damage in wooden structures, ensuring more accurate and reliable results.
Who does this training benefit?
The tutorial provides a comprehensive understanding of using wood damage FEM models to predict failure and assign stiffness degradation due to damage propagation in wood, making it a valuable resource for anyone involved in these areas. Additionally, it includes a detailed, step-by-step guide for Abaqus modeling and defining the desired criteria in the VUSDFLD subroutine. It can particularly help individuals interested in understanding and applying failure prediction models to wood materials. Specifically, it can benefit:
- Engineers and Researchers: they work in material science, structural engineering, and mechanical engineering which raises the need to predict failure in wooden structures.
- Students: Studying material science, mechanical engineering, or related fields who want to learn about failure prediction models and their practical applications.
- Professionals: In industries such as construction, aerospace, and automotive where wood or composite materials are used and understanding their failure mechanisms is crucial.
- Software Users: Those who use Abaqus or similar finite element analysis software and want to implement and validate custom subroutines for failure prediction.
Workshops for wood damage FEM analysis in Abaqus
In this tutorial, we have included five workshops to provide a step-by-step guide on using VUSDFLD for different wood failure criteria. We also check the results to ensure we have written the code correctly.
Workshop 1: Using the Sandhaas Model to Predict Failure in a Cubic Element
In the first workshop, we used Abaqus with the VUSDFLD subroutine to analyze failure initiation in a cubic element according to the Sandhaas criterion. We considered different loading and boundary conditions and examined the various criteria for the Sandhaas model. We demonstrated that failure occurs when the stress reaches the associated strength value for the material.
Workshop 2: Using the Hashin Model to Predict Failure in a Cubic Element
Workshop 2 is similar to the first one in terms of element size and boundary conditions. However, in this workshop, we define the Hashin model in the VUSDFLD subroutine to check different failure criteria. We considered various configurations to examine potential failures due to these criteria. Finally, we extracted the results to show that the material failed when one of the stress components reached the associated strength.
Workshop 3: Using the Balsa Model to Predict Failure in a Cubic Element
In the third workshop, we used the Balsa model to analyze failure in the same cubic element used in the first two ones. We considered two different loading conditions while capturing and discussing the failure criterion and damage parameters to ensure the subroutine functions as expected. Note that this model is less general compared to the Hashin and Sandhaas models. However, due to the numerous applications of Balsa wood in various fields, we included this criterion in our simulations for thoroughness.
Workshop 4: Using the Hashin Model to Predict Failure in a Wooden Part with a Hole
We based the first three workshops on very simple geometries (a single element) with straightforward loading and boundary conditions, primarily to verify whether the subroutines functioned as expected. However, in realistic problems, we encounter complex stress fields where multiple criteria may be satisfied simultaneously. To address such a scenario, we used the Hashin model to analyze the failure of a wooden part with a hole at its center. Due to the stress concentration adjacent to the hole, multiple criteria are satisfied in this region, presenting a more complex model compared to the previous workshops. This ensures that we can use the method effectively for simulating wood damage FEM in realistic examples.
Workshop 5: Using the Hashin Model to Predict Stiffness Degradation in a Cubic Element
The first four workshops focused solely on whether failure occurred or not. In other words, they predicted damage initiation but did not address its growth. In the final workshop, we used the Hashin model for the same single cubic element. However, this time, we defined stiffness degradation rules to reduce stiffness in the Abaqus material model based on the field variables calculated in the VUSDFLD subroutine. We then analyzed the results to show how damage initiates and reduces stiffness. This workshop demonstrates that we can extend the provided models by incorporating stiffness reduction in Abaqus to account for damage propagation in wood.
In conclusion, the provided workshops ensure that the subroutines work as expected. They provide a comprehensive understanding of using damage models to predict failure and assign stiffness degradation in wood damage Abaqus.
Reviews
There are no reviews yet