Abaqus convergence tutorial
Mastering convergence is crucial for getting accurate results from your Abaqus simulations, especially when dealing with nonlinear problems. This Abaqus convergence tutorial dives deep into the theory behind convergence and equips you with the skills to tackle it. You’ll learn how to identify different sources of nonlinearity and explore how they impact convergence. The practical workshops will guide you through simulating nonlinear behavior and investigating the convergence behavior of various numerical techniques, like Newton-Raphson and Quasi-Newton. By the end, you’ll be confident in achieving stable and reliable solutions for your complex Abaqus analyses.
Introduction
Most engineers and scientists studying physical phenomena are involved with two major tasks:
- Mathematical formulation of the physical process
- Numerical analysis of the mathematical model
Among the different numerical methods, Finite Element Method (FEM) has become an essential tool for engineers and designers as it offers numerous benefits and advantages over traditional methods of problem-solving. These advantages include:
- Accurate and Precise Results
- Time-Saving
- Cost-Effectiveness
- Versatility
- Optimization
- Future-Proofing
Abaqus is a powerful finite element analysis (FEA) software that can be used to solve a wide variety of engineering problems. These problems can range from simple linear problems, such as calculating the stress in a beam under a load, to complex nonlinear problems, such as simulating the collapse of a building under an earthquake.
Nonlinear problems in Abaqus encompass a wide range of physical phenomena that exhibit a departure from linear behavior. These problems involve material or system responses that are not proportional to the applied loads, resulting in complex and often unpredictable outcomes.
In Abaqus, nonlinear problems are characterized by material properties or boundary conditions that vary with deformation, load magnitude, or other parameters.
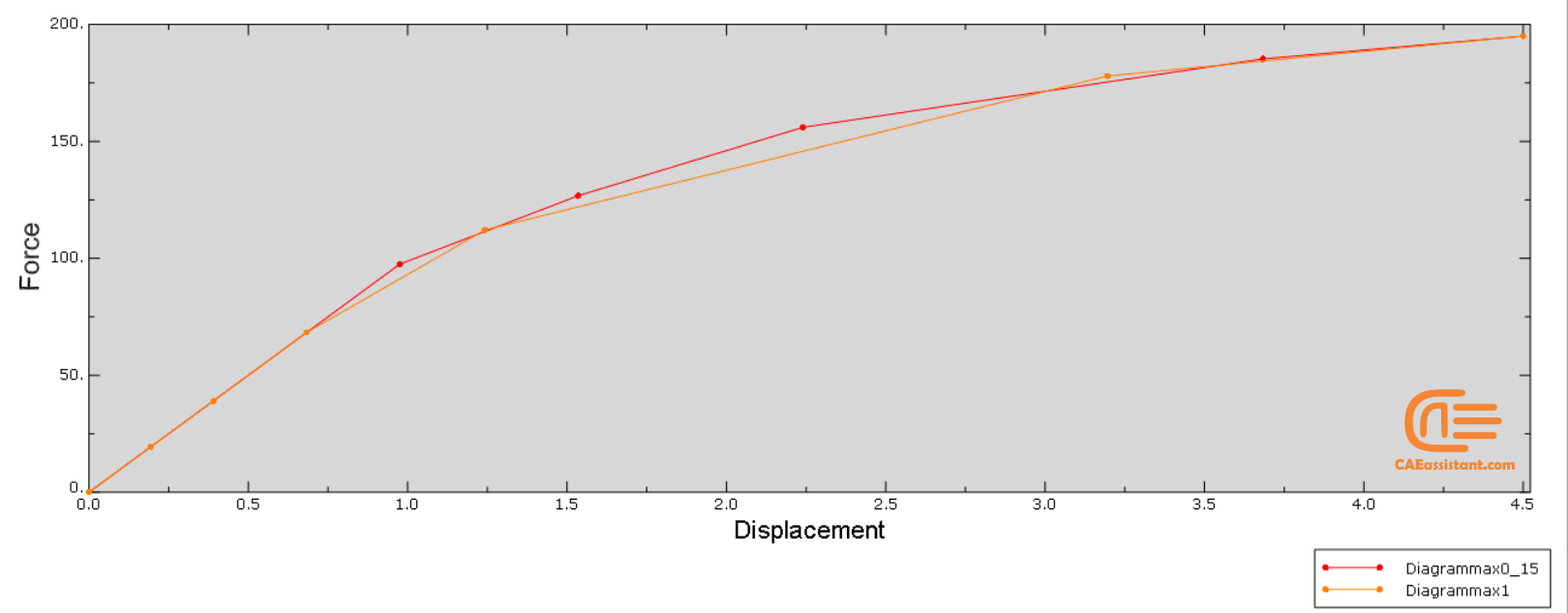
One of the critical aspects of using Abaqus is ensuring the convergence of the solution, which is the process of reaching a stable and accurate result. In Abaqus, convergence is typically measured by monitoring the residuals of the governing equations, such as the force balance and the displacement equilibrium. The residuals represent the imbalance in the equations and should decrease as the solution converges. Here we want to provide a comprehensive understanding of solution convergence in Abaqus and its importance. (Abaqus convergence tutorial)
What is Convergence in FEA?
Solution convergence in Abaqus is a critical aspect of numerical simulation to ensure the accuracy and reliability of the results. Convergence refers to the process by which the solution approaches a consistent and stable value as the simulation progresses.
In FEA “convergence” can imply multiple meanings such as:
• Mesh convergence
• Time integration accuracy
• Convergence of nonlinear solution procedure
• Solution accuracy
Each one of these convergence meanings is completely discussed in this chapter. (Abaqus convergence tutorial)(Abaqus convergence tutorial)(Abaqus convergence tutorial)(Abaqus convergence tutorial)
What is a Nonlinear problem?
Nonlinear problems are those in which the material behavior or the loading conditions are not linear. This means that the relationship between stress and strain is not a straight line, or that the loading conditions vary throughout the analysis.
Nonlinear problems are an important part of engineering analysis. Abaqus provides a powerful set of tools that can be used to solve a wide variety of nonlinear problems. By understanding the different types of nonlinear problems and the tools available in Abaqus, users can successfully solve even the most complex nonlinear problems.
There are three common sources of nonlinearity:
- Geometry
These arise when the deformation of a structure significantly alters its geometry, affecting the load paths and deformation patterns. For example, the buckling of a slender beam or the large-scale deformation of a soft tissue.
- Material
These involve materials with stress-strain relationships that are nonlinear, such as plastic deformation of metals, creep of polymers, or strain softening of concrete.
- Boundary
Occurring when surfaces interact, leading to complex contact forces and deformation patterns. These are often encountered in simulations involving friction, impact, or assembly processes.
Various types of nonlinearities will be discussed through simple examples in this chapter.
Properties of Linear and Nonlinear Problems
Linear and nonlinear problems are two broad categories of mathematical and scientific problems that are encountered in various fields such as physics, engineering, economics, and computer science. The distinction between these two types of problems lies in the nature of the relationships between the variables involved. Understanding the properties of linear and nonlinear problems is crucial for selecting appropriate methods and techniques to solve them.
Linear problems have the following features:
- Existence
For each load F there will always be at least one solution u.
- Uniqueness
For each F there will always be only one solution u!
- Scaling
If F causes a displacement u, then aF causes a displacement au.
- Superposition
If F causes a displacement u and G causes a displacement v, then F + G causes a displacement u + v.
Nonlinear problems have the exact opposite features and an additional one:
- History Dependent
In a nonlinear problem, the “unique” solution u at time t is determined by the entire load history of P(t).
Numerical Techniques for Solving Nonlinear Problems
Numerical methods offer efficient and reliable approaches to obtaining accurate solutions for complex systems and scenarios. These techniques provide approximate numerical solutions to nonlinear problems, where analytical solutions may not be readily available. Two of the most common techniques discussed in this chapter:
- Newton-Raphson method
The Newton-Raphson method is a popular iterative technique for finding the roots of a nonlinear equation. The method is based on the idea of approximating the function with a linear function at each iteration and then using the linear approximation to find a better estimate of the root. The process continues until the desired level of accuracy is achieved. Newton’s method is particularly useful for solving nonlinear equations with a single variable, and it converges rapidly when the initial guess is close to the actual root. (Abaqus convergence tutorial)
- Quasi-Newton method
Quasi-Newton methods are a class of optimization algorithms that approximate the Hessian matrix of the function using only first-order information. The method involves iteratively updating the Hessian approximation and using it to find a better estimate of the minimum. Quasi-Newton methods are particularly useful for solving large-scale optimization problems, as they can handle non-differentiable functions and do not require the computation of second-order derivatives.
Implementing these methods in Abaqus simulations (Abaqus convergence tutorial) is covered in this chapter and the workshops of this package.














Reviews
Clear filtersThere are no reviews yet.