Introduction to Creep | Creep Abaqus modeling
One of the important issues in studying mechanical systems is determining the service life of their components. Engineers need to be aware of the time to failure of system components to prevent extensive damages. As you may know, one of the causes of mechanical component failure is the creep phenomenon.
Creep is a phenomenon in materials science and engineering where gradual deformation or strain occurs over time under a constant load or stress, particularly at elevated temperatures. Understanding and analyzing creep behavior is of significant importance in various industries, including power generation, aerospace, and manufacturing. Creep analysis allows engineers to predict the long-term deformation and potential failure of materials, enabling the design of structures and components that can withstand these conditions. Therefore, determining the life of components subjected to creep is of great importance.
Lesson 1: What is Creep?
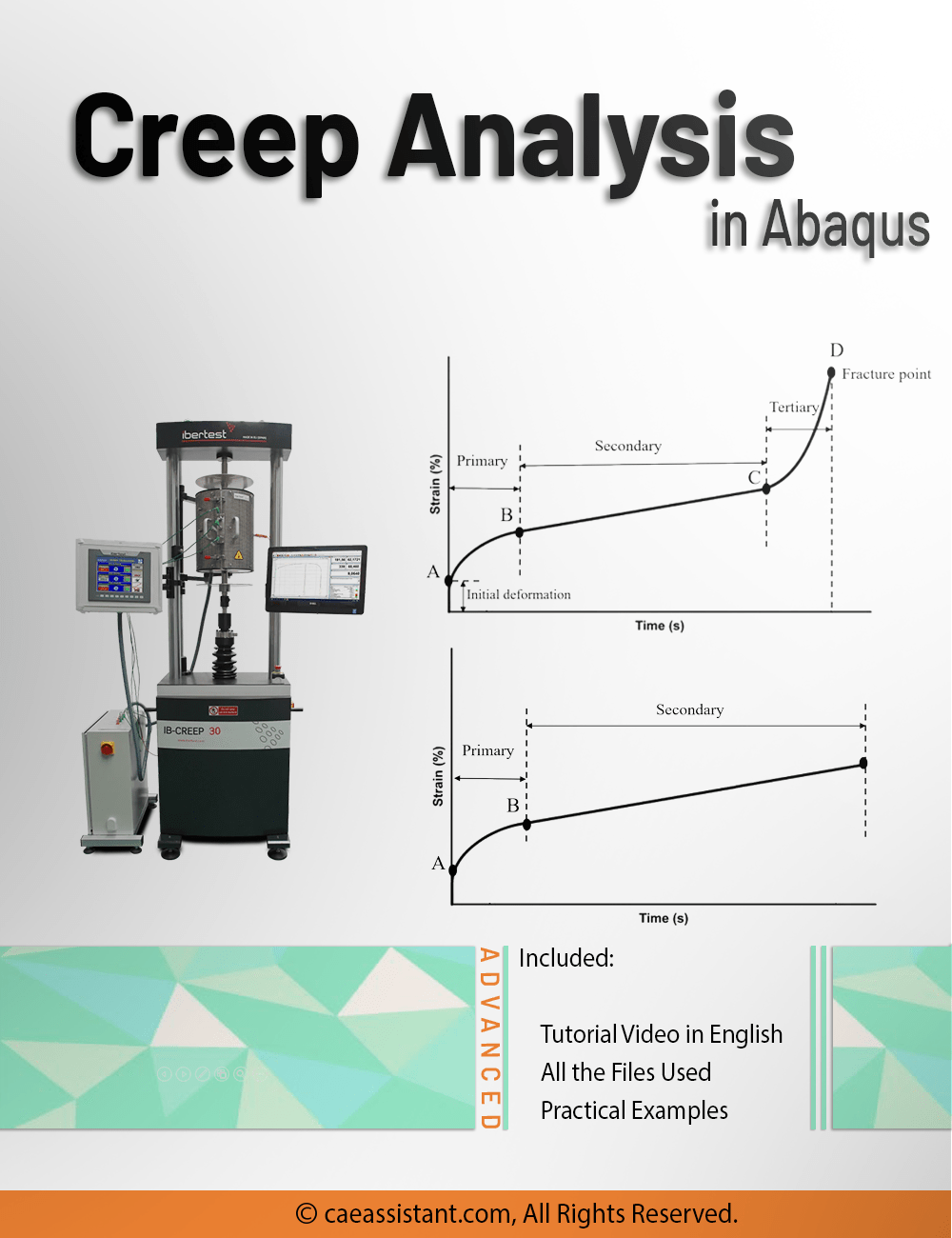
In this lesson, first, the creep phenomenon is defined: Creep is time-dependent deformation of a material, and it typically occurs at high temperatures and under constant stress. These stresses are usually lower than the yield stress. Therefore, we can consider three influential factors on creep: time, temperature, and stress level. Since many industrial components operate under constant stress lower than the yield stress and in high-temperature environments, numerous industrial components experience failure due to creep phenomenon. Therefore, the investigation and simulation of the creep phenomenon are of great importance.
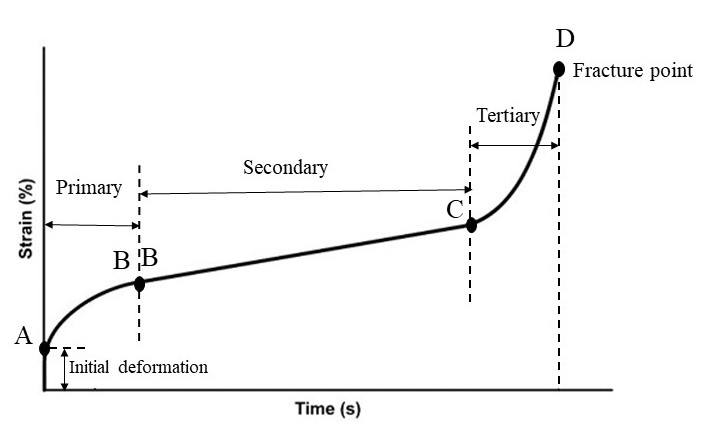
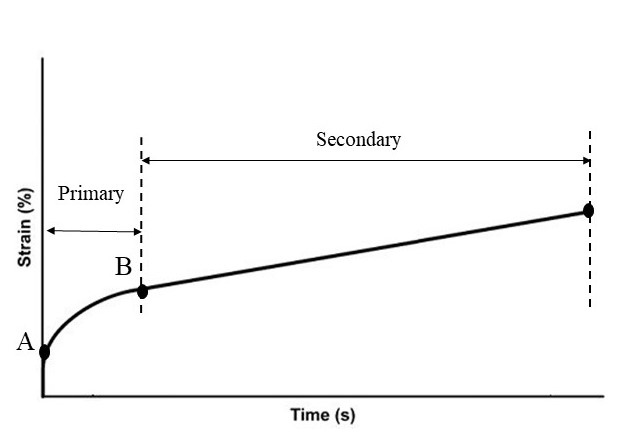
Moreover, you will learn more about the temperature factor: The first temperature effect is Vacancy Concentration. In crystalline materials, some atoms are missing from their intended positions in the lattice. These defects in the crystal lattice are called vacancy Concentration. Increasing temperature leads to an increase in the concentration of vacancies, and an increased concentration of vacancies aids the creep process. Also, the creep curve will be discussed, which helps you to better understand the stages of creep. Usually, the strain-time diagram is used to study the creep process. To examine this diagram, you should know the standard creep test methods. The standard creep test is generally performed in two ways: constant load and constant stress. In first method, only a constant load is applied to the sample and the amount of load does not change over time. In the second method, which requires advanced equipment, a constant stress is applied. In this method, considering that the cross-sectional area of the sample is constantly decreasing during the test, the force must also decrease in order to keep the stress constant.
Lesson 2: What are creep life estimation models?
Engineers need to be aware of the time to failure of system components to prevent extensive damages. As you may know, one of the causes of mechanical component failure is the creep phenomenon. In this section, you will study methods for determining the life of components under creep: Larson-Miller, Orr-Sherby-Dorn, and Polynomials estimation models.
Lesson 3: What are creep models?
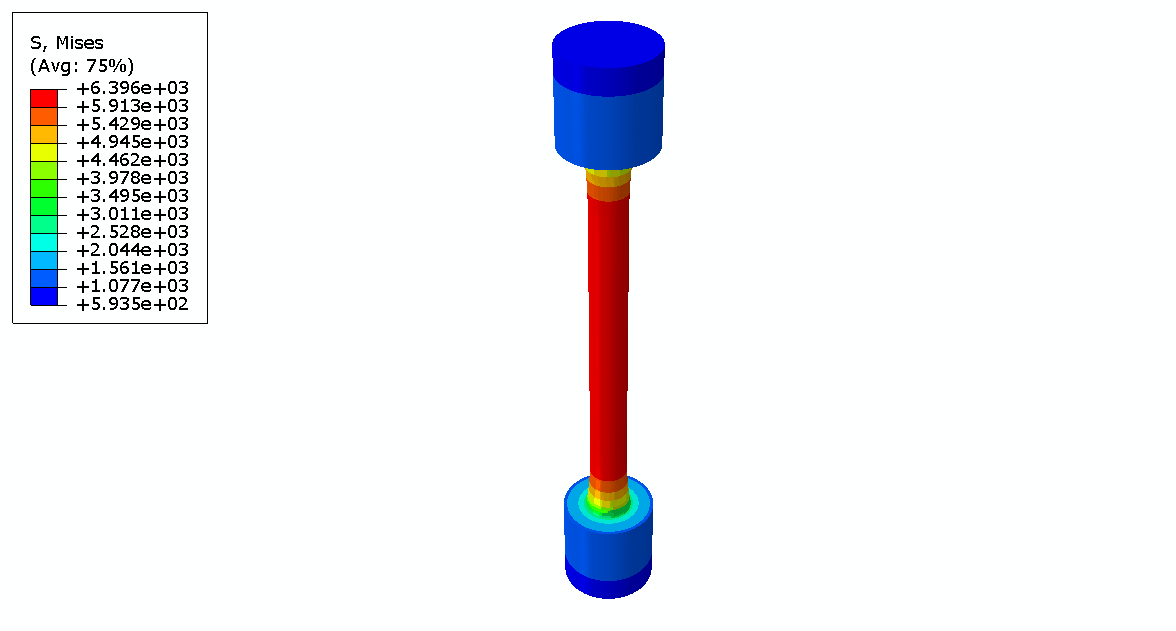
There are several models to simulate the creep behavior with and in this lesson, you will learn all the models in the Abaqus. Simulation of creep behavior in Abaqus, provides valuable insights into material response under sustained loads and high temperatures. Abaqus offers sophisticated creep modeling capabilities that enable engineers to accurately predict creep deformation and assess the structural integrity of components over time. In Abaqus, creep can be simulated using various creep models:
- Time-Hardening law: When dealing with loading conditions where the stress or temperature is changing, it is necessary to have a proper hardening relation to accurately models the material behavior. However, in general, it is not recommended to use the time hardening relation when the stress is changing.
- Time-Power law: The time-power law is equivalent to the time hardening law but with modifications to avoid computational problems.
- Strain-Hardening law: This law is suitable for modeling the creep behavior under changing stress conditions. However, similar to the time hardening law, it is more appropriate for low stress levels.
- Power law: The power law is equivalent to the strain hardening law with some slight differences.
- Hyperbolic-Sine law: The hyperbolic sine law, along with the subsequent laws, effectively models creep due to their consideration of the effects of temperature, stress, and time.
- Anand law
- Darveaux law
- Double Power law
These models capture the time-dependent behavior of materials by incorporating parameters like creep exponent, activation energy, and reference stress. Also, if you need another model or a user-defined creep model, you can use the Creep subroutine, which will be explained in workshop 2. Moreover, according to the Abaqus documentation, none of the above models are suitable for modeling the creep cyclic loading, which leaves us with only one option and that is the Creep subroutine.




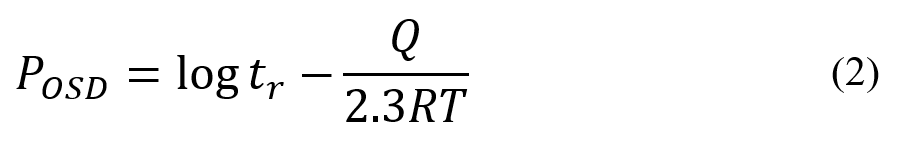
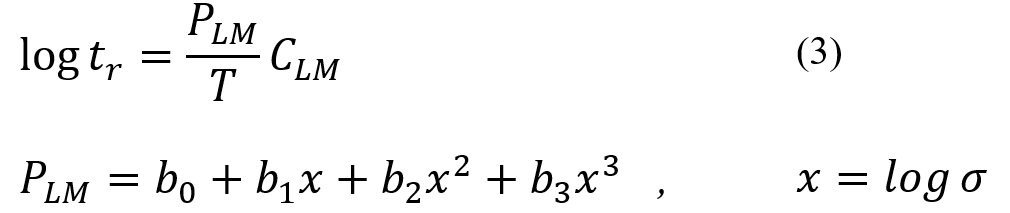
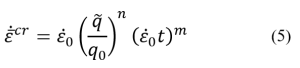
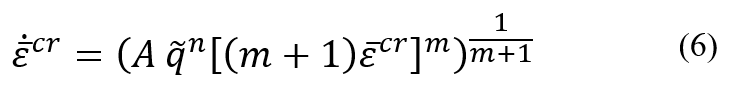
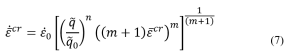















Olga –
I purchased the Creep Analysis in Abaqus training package, and I am extremely satisfied with it. This package provides a comprehensive guide to creep analysis using the Abaqus software. It covers various methods for estimating creep life in system components, such as the Larson-Miller method. . The content is presented clearly and is easy to understand, accompanied by practical examples that demonstrate the best practices for conducting creep simulations. I highly recommend this package to engineers working in the field of creep analysis.
Experts Of CAE Assistant Group –
Thanks for your kind feedback
Rinaldo –
Thank you very much for this outstanding package. Everything was well-explained, and I was able to use it easily. The sections on result analysis and output review were particularly helpful. Do you plan to offer more advanced educational courses? I am interested in learning more about creep analysis and material behavior under various conditions.
Fiammetta –
Using this package was truly excellent. Everything was well-explained, and I was able to perform creep analysis effortlessly. The sections on default settings and material definitions were particularly helpful. Do you have any guides for more advanced analyses and detailed explanations on setting creep parameters? I’m looking for more complex analyses, and any additional guidance would be beneficial.
Leandro –
This tutorial package helped me perform creep analysis in Abaqus effortlessly. Your explanations on defining creep parameters and model settings were very precise and clear.
Vittoria –
The package was very useful, and I managed to complete my project on time. Your explanations on defining materials and creep parameters were very clear and understandable. Can you provide more guidance on advanced creep parameters and their impact on final results?
Ettore –
I was very satisfied with this package. Everything was well-explained, and I was able to use it easily. The sections on initial settings and boundary conditions were very helpful. Do you have plans to offer other tutorial packages in the future? I am particularly interested in dynamic analyses.