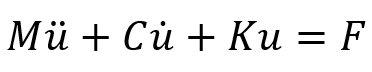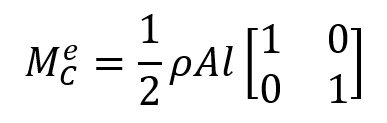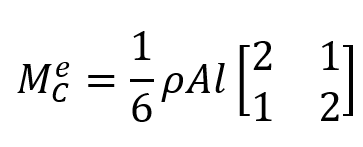The finite element method (FEM) is a powerful tool used in Abaqus software, and a crucial concept within it is “Abaqus mass.” While stiffness and other parameters often take center stage, understanding the role of mass in Abaqus is vital for accurate and insightful simulations.
Mass is the primary factor dictating an object’s inertia and its resistance to changes in motion. In Abaqus FEA, this translates to the object’s response to external forces, whether it be a sudden impact, periodic vibrations, or the application of varying loads. By correctly incorporating the Abaqus mass distribution, we can accurately simulate the object’s dynamic response.
Another important mass impact on analysis is the weight force that will be entered into your model if the mass of the structure can not be ignored. This mass can be structural mass or non-structural mass. So, not only the dynamic but also the static analyses care about the mass.
In this article, we will talk about the mass importance in FEM and the different terms related to mass in the finite element analyses. Let’s start.
1. What is Mass and Why Does it Matter in FEM?
In the context of FEM, mass represents the inertia of the system. Understanding of mass’s role in FEA is essential for successful engineering simulations. By correctly modeling mass distribution, using appropriate techniques, and carefully choosing the level of detail, engineers can achieve reliable and accurate results.
Here are some reasons why mass is important in FEA:
- Dynamic Analysis
When analyzing structures subjected to time-dependent loads or vibrations, mass is critical. It determines the system’s natural frequencies and modes of vibration, crucial for predicting resonance and ensuring structural stability.
- Transient Analysis
For understanding the system’s behavior over time, mass is crucial. It governs the momentum and kinetic energy of the system, affecting the response to transient loads like impacts or explosions.
- Wave Propagation
In problems involving wave propagation, like acoustic analysis or seismic studies, mass is essential. It dictates the speed and direction of wave propagation, influencing the system’s response to disturbances.
- Heat Transfer
While less obvious, mass also plays a role in heat transfer problems. It influences the thermal inertia of the system, affecting the rate at which it absorbs or releases heat.
In FEM, the equation of motion for a mass-damper-spring system is written as the below equation:
In this equation, the coefficient of is the mass matrix, M, the coefficient of
is the damping matrix, C, and the coefficient of
is the stiffness matrix, K. F also forms the force vector.
,
,
and are respectively the displacement, velocity, and acceleration vectors.
The mass matrix is a symmetric matrix which is usually introduced in two ways:
- Consistent mass matrix
- Lumped mass matrix
Let’s see what is the difference between these two.
1.1. Lumped Mass Matrix
This approach simplifies calculations by assigning all mass to the nodes of the elements. While computationally efficient, it can be less accurate in some cases, particularly for complex geometries or high-frequency vibrations.
The total mass of an element is directly apportioned to nodal freedoms, ignoring any cross-coupling. The goal is to build a diagonally lumped mass matrix “DLMM”, denoted here by .
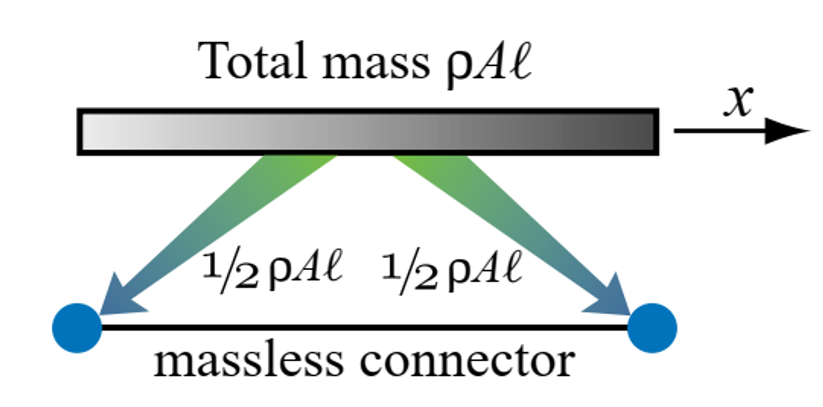
As the simplest example, consider a 2-node prismatic bar element with length l, cross-section area A, and mass density ρ, which can only move in the axial direction x, as shown in figure 1. The total mass of the element is . This is divided into two equal parts and assigned to each end node to produce
as below:
Figure 1: Direct mass lumping for 2-node prismatic bar element
1.2. Consistent mass matrix
This method distributes mass more realistically across the element, leading to more accurate results, especially for higher-order elements or complex problems. However, it requires greater computational effort.
Again, consider the 2-node prismatic bar element moving along x, the consistent mass matrix “CMM” which is denoted here by is equal to:
The choice between lumped and consistent mass matrices depends on the specific problem and the desired level of accuracy. The lumped mass matrix is easily invertible due to its diagonal nature, making calculations easier, but it has slightly lower computational accuracy compared to the consistent matrix.
In order to get more familiar with the mass matrix and other structural matrices and also the way to generate these matrices from your Abaqus model, we recommend seeing the following link:
Now let’s see how to enter mass and related loads like gravity load in our analysis in Abaqus.
2. Abaqus mass modeling
The Abaqus mass of the model in your analysis can be divided into two groups: structural and non-structural mass. In the following sections, we will talk about them.
2.1. Abaqus structural mass
In FEM, the structural mass is typically characterized using the mass matrix, which is a sparse matrix that represents the distribution of mass in the structure. The mass matrix is obtained by discretizing the structure into a set of finite elements and then computing the mass matrix for each element based on its shape, size, and material properties. The elemental mass matrices are then assembled to form the global mass matrix, which describes the mass distribution for the entire structure.
A “structural” mass is defined as the sum of all the mass contributions to an element outside of the nonstructural features. This may include the mass due to any material definitions associated with the element; any “mass per unit area” given on the section definition for shell, membrane, and surface elements; mass from any rebars included in shell, membrane, and surface elements; and any additional inertia given on the section definition of beam elements. A nonstructural mass contribution to an element is ignored if that element has no structural mass.
In simple words, when you have a model, it has a volume. This model is made out of a material which has a mass density. The total mass of the model is obtained as the product of volume and mass density. This total mass will be distributed in the finite element model and it will be considered as the structural mass of the model.
But what is the non-structural mass?
2.2. Abaqus non-structural mass
Non-structural mass refers to elements within a structure that do not contribute to its load-bearing capacity but still possess significant weight such as paint on sheet metal panels in a car. It can be used to bring the net mass of one or more components in the model up to a known value.
Non-structural mass can be positive to add mass to the model and negative to remove mass from the model, with the corresponding increase or decrease in the element stable time increment in an Abaqus/Explicit analysis.
The Abaqus mass contribution from nonstructural features can be included in the model even if the features themselves are omitted. The nonstructural mass is smeared over an element set that is typically adjacent to the nonstructural feature. This element set can contain solid, shell, membrane, surface, beam, pipe, or truss elements.
A given element in the model can have contributions from multiple nonstructural mass specifications. The nonstructural mass in a given element will participate in any mass proportional distributed loads, such as gravity loading, defined on that element. When a nonstructural mass is added to a shell, beam, or pipe element with active rotational degrees of freedom, the nonstructural contribution affects both the element mass and the element rotary inertia.
The element stable time increment increases with a positive nonstructural mass and decreases with a negative nonstructural mass. In general, it is easier to use a nonstructural mass definition to bring an additional mass into the model than to do the same with a group of point masses. It is also more beneficial in an Abaqus/Explicit analysis due to a possibly higher time increment.
3. Defining Abaqus’s non-structural mass
To define a nonstructural mass contribution to the model mass, you must first identify the region over which the contribution must be added. You then specify the value of the nonstructural mass using the appropriate units and, if the total mass from the nonstructural features is known, determine how the nonstructural mass is distributed over the region.
3.1. Specifying the units of the nonstructural mass
The nonstructural mass can be specified in different types of units, depending on the types of elements contained in the specified region.
3.1.1. Specifying units of mass
A total nonstructural mass with units of “mass” can be spread over a region containing solid, shell, membrane, beam, pipe, and/or truss elements. For this purpose, you must do the following:
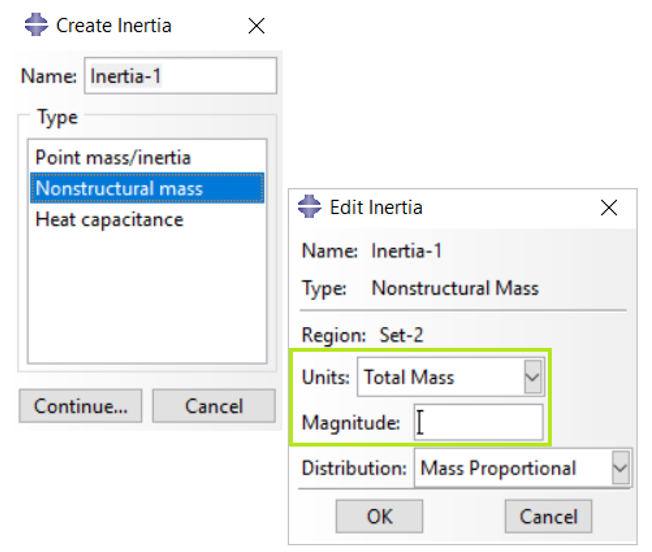
Property or Interaction module: Special > Inertia > Create: Nonstructural mass: select region: Units: Total Mass: Magnitude: total mass of the nonstructural feature
Figure 2: Specifying the units of mass as non-structural mass in Abaqus
3.1.2. Specifying units of mass per unit volume
A nonstructural mass with units of “mass per unit volume” can be spread over a region containing solid, shell, membrane, beam, pipe, and/or truss elements. For this purpose, you must do the following:
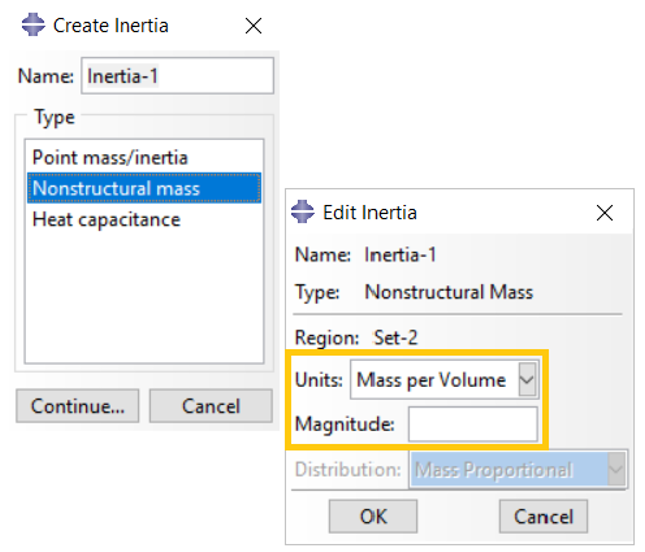
Property or Interaction module: Special > Inertia > Create: Nonstructural mass: select region: Units: Mass per Volume: Magnitude: added density due to the nonstructural feature
Figure 3: Specifying the units of mass per unit volume as non-structural mass in Abaqus
3.1.3. Specifying units of mass per unit area
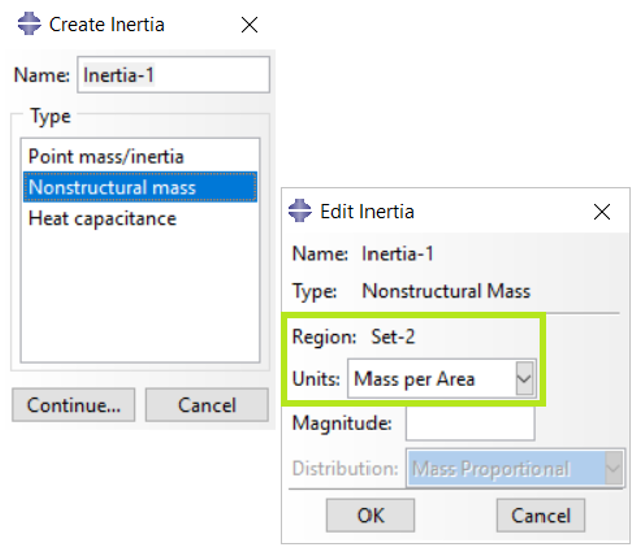
A nonstructural mass with units of “mass per unit area” can be spread over a region containing conventional shells, membranes, and/or surface elements. For this purpose, you must do the following:
Property or Interaction module: Special > Inertia > Create: Nonstructural mass: select region: Units: Mass per Area: Magnitude: added mass per unit area due to the nonstructural feature
Figure 4: Specifying the units of mass per unit area as non-structural mass in Abaqus
3.1.4. Specifying units of mass per unit length
A nonstructural mass with units of “mass per unit length” can be spread over a region containing beam, pipe, and/or truss elements. For this purpose, you must do the following:
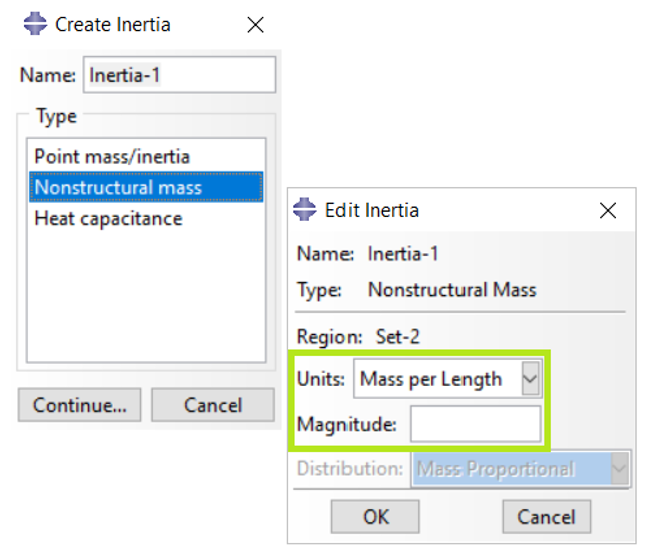
Property or Interaction module: Special > Inertia > Create: Nonstructural mass: select region: Units: Mass per Length: Magnitude: added mass per unit length due to the nonstructural feature
Figure 5: Specifying the units of mass per unit length as non-structural mass in Abaqus
3.2. Controlling the distribution of the total mass from nonstructural features
There are two methods available for distributing the nonstructural mass over the region when the total mass from the nonstructural features is known.
3.2.1. Distributing the nonstructural mass in proportion to the element’s structural mass
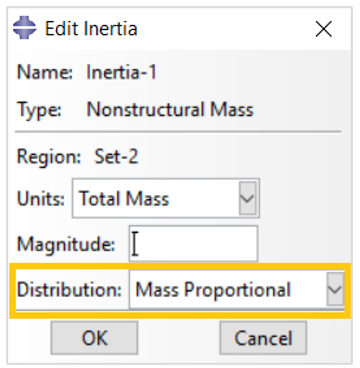
If you do not want to change the center of mass for the region, distribute the nonstructural Abaqus mass in proportion to the element’s structural mass. This method results in a uniform scaling of the structural density of the region. Abaqus uses mass proportional distribution by default.
Figure 6: Selecting mass proportional distribution for total mass
3.2.2. Distributing the nonstructural mass in proportion to the element volume
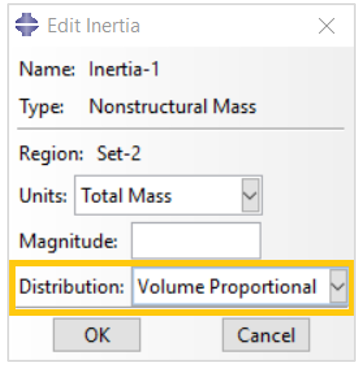
Alternatively, you can distribute the nonstructural mass in proportion to the element volume in the initial configuration. This method results in a uniform value added to the underlying structural density over the region. Therefore, the center of mass for the region may be altered if the region has nonuniform structural density.
Figure 7: Selecting volume proportional distribution for total mass
For entering mass into your model, there is another option called “Point Mass”. Let’s see how it works.
4. Abaqus Point Mass
You can enter some masses which are concentrated at a point in your model. Mass elements allow the introduction of concentrated mass that is either isotropic or anisotropic at a point. They are associated with the three translational degrees of freedom at a node. But how to enter point mass in Abaqus?
4.1. Defining the isotropic mass value
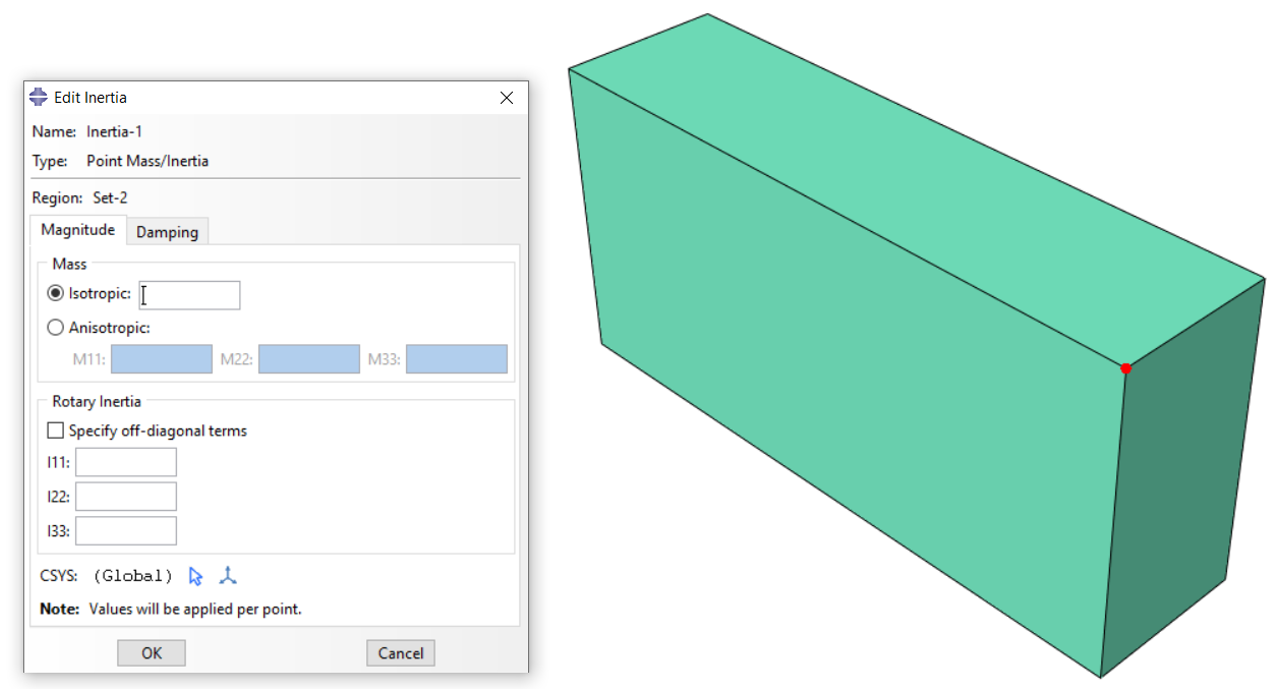
You specify a mass magnitude, which is associated with the three translational degrees of freedom at the node of the element. Specify mass, not weight. You must associate this mass with a region of your model. For this purpose, you must do the following:
Property or Interaction module: Special > Inertia > Create: Point mass/inertia: select point: Magnitude: Isotropic: mass magnitude
So, you need to determine a point where mass is going to be put and also the mass magnitude (Figure 8).
Figure 8: Defining the isotropic mass value as a point mass in Abaqus
4.2. Defining the anisotropic mass tensor
You can specify the mass as anisotropic by giving the three principal values and the principal directions. When the orientation of the principal directions is not specified, they are assumed to coincide with the global axes. In a large-displacement analysis, the local axes of the anisotropic mass rotate with the rotation, if active, of the node to which the anisotropic mass is attached. The rotation degree of freedom is active at a node if that node is connected to a beam, a conventional shell, a rotary inertia element, or a rigid body.
You can specify mass proportional loads such as gravitation on an anisotropic mass. Damping and mass scaling can also be used with an anisotropic mass. Specify mass, not weight. You must associate this mass with a region of your model. For this purpose, you must do the following:
Property or Interaction module: Special > Inertia > Create: Point mass/inertia: select point: Magnitude: Anisotropic: ,
and
As the final section of this article, let’s see how to define gravity load in Abaqus which was also mentioned here.
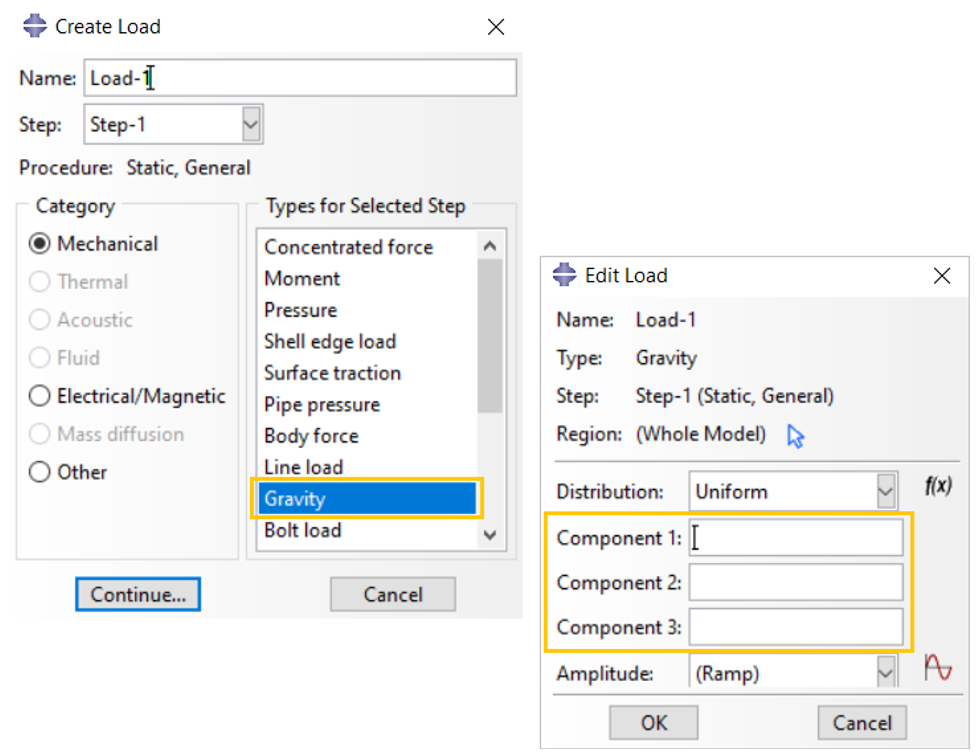
5. Abaqus Gravity load
You can create a gravity load to define a uniform acceleration in a fixed direction. A gravity load is applied to the whole model. Abaqus calculates the loading using the acceleration magnitude that you enter in the gravity load definition and the density specified in the material definition (Figure 9).
Figure 9: Defining gravity load in Abaqus
- If you are working in three-dimensional or two-dimensional space, the Component 1, Component 2, and Component 3 fields correspond to the 1-, 2-, and (if applicable) 3-directions.
- If you are working in axisymmetric space, only the Component 2 text field is available. Component 2 corresponds to the axial direction.
And this is the end of this article. Let’s summarize what we learned from this post.
6. Summary
We started our discussion by determining the mass importance in Abaqus and talked about the different mass matrices you may encounter in finite element methods. Then we talked about the structural and non-structural mass. Different ways to define non-structural mass (Abaqus mass) in the Abaqus model are mentioned in detail. The point mass as another way to input mass in the model was also discussed. In the final section, the Abaqus gravity load, which turns the system mass into the force in the analyses, is introduced briefly.
In the end, we appreciate for reading this article. Don’t forget to leave us your comments about this article to improve our content quality. Wish you the Best.
It would be helpful to see Abaqus Documentation to understand how it would be hard to start an Abaqus simulation without any Abaqus tutorial.
7. Users ask these questions
As we said, defining mass in Abaqus is an important thing in both dynamic and static analyses; so there is no wonder Abaqus users ask questions about it a lot. Therefore, we decided to answer a few of them which you can see below:
I. Mass and gravity
Q: I have a model of a building in which I have already defined the structural and non-structural masses. Structural masses are defined through the density of the material while the non-structural masses are defined as point masses. In this step, I want to perform the modal analysis. In the subsequent steps, I want to define a static analysis and later a dynamic analysis(earthquake). During the static analysis, I want to exploit the gravity load for the structural mass while I want to use distributed pressure for the non-structural. But if don’t remove the point masses I would consider it twice. In the subsequent step, I need these masses for the dynamic analysis. To resume, I have to apply the point masses in the first step, remove from the second, and put in the third. Is it possible? When I try to do this from one step it’s immediately eliminated from all the steps.
A: Greetings,
You cannot activate and deactivate mass in any step. In other words, either you define mass or not for the whole analysis. But it’s different when it comes to the Gravity load. You can activate or deactivate the gravity load through the load manager dialog box in any step you want.
I hope this will help you.
Best wishes.