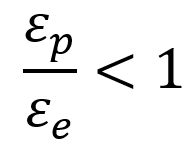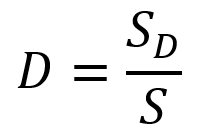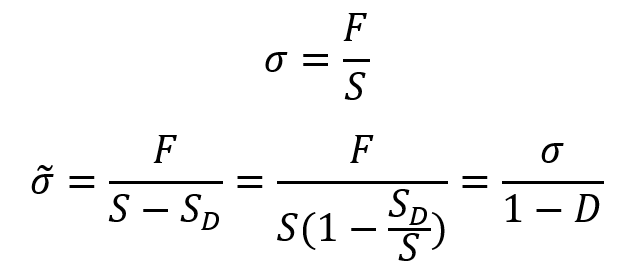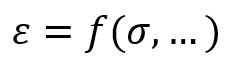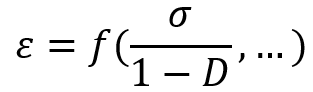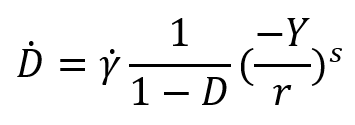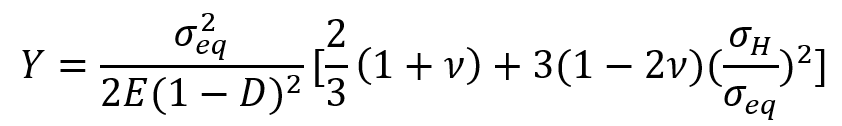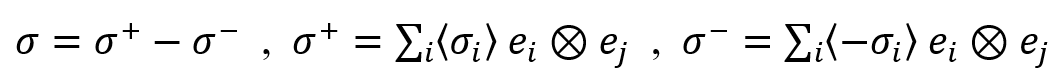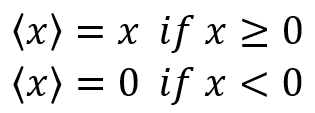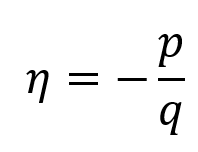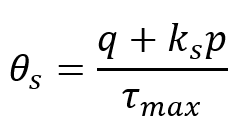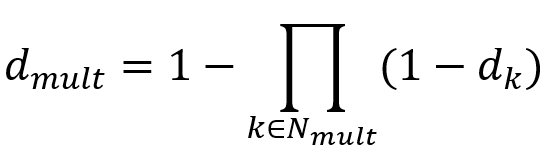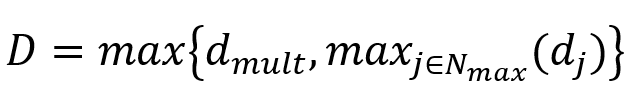Ductile damage, a phenomenon that has been the subject of extensive research in the field of materials science, refers to the progressive degradation of a material’s mechanical properties due to the accumulation of microscopic defects. This process is particularly relevant in the context of metal alloys, which are widely used in various industries due to their strength, durability, and ductility. Understanding ductile damage is crucial for predicting the service life of structures and components, as well as for designing materials with improved resistance to failure.
Ductile damage is a complex process that involves several stages, including the initiation, growth, and coalescence of microscopic voids within the material. Researchers have developed a variety of methods for predicting and quantifying this phenomenon. These methods typically involve the use of computational models, which can simulate the initiation, growth, and coalescence of voids within a material under various loading conditions.
By this mentality, we start our discussion with basic concepts like damage definition, damage types, etc. Then we head toward theories, applications, and ductile damage in Abaqus.
1. What is Damage in mechanical engineering?
The damage of materials is the progressive physical process by which they break. All materials are composed of atoms, which are held together by bonds resulting
from the interaction of electromagnetic fields. When debonding occurs, this is the beginning of the damage process.
At the microscale level, this is the accumulation of micro stresses in the neighborhood
of defects or interfaces and the breaking of bonds, which both damage the material.
At the mesoscale level of the representative volume element (RVE), this is the growth and the coalescence of microcracks or microvoids which together initiate one crack.
At the macroscale level, this is the growth of that crack. The two first stages may be studied using damage variables of the mechanics of continuous media defined at the mesoscale level. The third stage is usually studied using fracture mechanics with variables defined at the macroscale level.
You may wonder what are these scales? Let’s define them from the smallest to the biggest.
- The microscale is the scale of the mechanisms used to consider strains and damage.
- The mesoscale is the scale at which the constitutive equations for mechanics analysis are written.
- The macroscale is the scale of engineering structures.
Figure 1: Damage progressive process
1.1. Ductile damage vs Brittle damage
The damage is called brittle when a crack is initiated at the mesoscale without a large amount of plastic strain. Just to give an order of magnitude, let us say that the ratio of plastic strain to elastic strain is below unity:
On the other hand, the damage is called ductile when it occurs simultaneously with plastic deformations larger than a certain threshold . It results from the nucleation of cavities due to decohesions between inclusions and the matrix followed by their growth and their coalescence through the phenomenon of plastic instability. Particularly damage models in ductile metals are proposed, and the Lemaitre model will be discussed.
1.2. Mechanical Representation of Damage
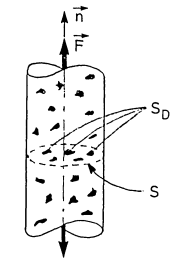
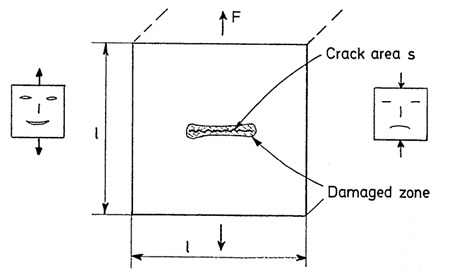
Consideration of the simple one-dimensional case of a homogeneous damage pictured in Figure 2 leads to the simple definition of damage as the effective surface density of microdefects:
Figure 2: One-dimensional damaged sample under tension
S in this equation is the surfaces free of microcracks or microcavities and is the surface of microcracks or microcavities. It is convenient to introduce an effective stress
related to the surface that effectively resists the load, namely
:
This definition is the effective stress on the material in tension. In compression, if some defects close, the damage remaining unchanged, the surface that effectively resists the load is larger than . In particular, if all the defects close, the effective stress in compression is equal to the usual stress
.
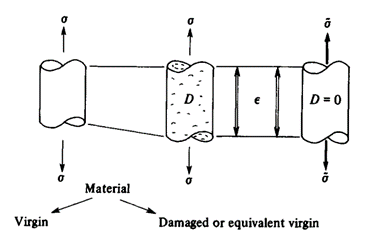
Lemaitre stated the ‘Strain Equivalent Principle’ for damage which says:
“Any strain constitutive equation for a damaged material may be derived in the same way as for a virgin material except that the usual stress is replaced by the effective stress”.
Is it complicated? Let’s say it in a simpler way.
Consider an undamaged material for which D = 0. Assume a constitutive equation for this material which is the relation between strain and stress like:
Now consider a damaged material for which . The Strain Equivalence Principle says that the constitutive equation remains unchanged but instead of
you must use
in this equation.
A schematic of this statement is shown in figure 3.
Figure 3: Schematic of Strain Equivalent Principle
2. Delve into the world of Continuum Damage Mechanics
Continuum damage mechanics (CDM) is a theoretical framework for describing the progressive degradation and failure of materials under various loading conditions. It treats damage as a continuous distributed parameter that represents the loss of material integrity. By employing mathematical models, CDM aims to predict the evolution of damage and material response, providing valuable insights into the failure mechanisms and structural integrity of materials.
CDM is based on the assumption that damage is a continuous field variable that can be described by a set of state variables. These state variables can be used to track the evolution of damage in the material over time. The most common state variables used in CDM are the damage variable, which represents the fraction of the material that is damaged, and the damage strain, which represents the amount of strain that has been caused by damage.
2.1. Damage Evolution
The evolution of the damage internal variable is assumed to be governed by the relation:
Where is the accumulated plastic strain, r, s are material constants, The quantity Y is the damage energy release rate with the following relation:
Where is the von Mises equivalent stress,
is the hydrostatic stress,
and
are the Poisson’s ratio and the Young’s modulus of the undamaged material respectively.
is the triaxiality ratio, which plays a very important role in the rupture of materials, the measured ductility at fracture decreases as it increases. Remember what is known from practice: “High triaxiality makes materials brittle!”
2.2. Crack Closure Effect
For certain materials and certain conditions of loading, the defects may close in compression. This is often the case for very brittle materials. If the defects close completely, the area that effectively carries the load in compression is no longer .
In fact, the real defects of complicated shapes do not close completely. The effective area in compression is such that
.
Let us write this expression as: . where h,
is a crack closure parameter which depends a priori upon the material and the 1oading.
Figure 4: Crack opening and crack closure under tension and compression loadings
For the crack closure effect, the compressive/tensile additive split of the stress tensor:
Where and
are respectively the tensile and compressive components of
.
The numerical prediction of material degradation, based on the damage model without crack closure effects, is not in agreement with experimental evidence, which shows that only a relatively small damage accumulation results from the process.
You can also see the Mac Auley brackets used in this expression which says:
After this brief review of continuum ductile damage, let’s head toward Abaqus ductile damage. Take a rest and when you are ready, we will continue.
3. How to define Abaqus Ductile Damage?
Abaqus offers a general framework for material failure modeling that allows the combination of multiple failure mechanisms acting simultaneously on the same material. Material failure refers to the complete loss of load-carrying capacity that results from progressive degradation of the material stiffness. The stiffness degradation process is modeled using damage mechanics.
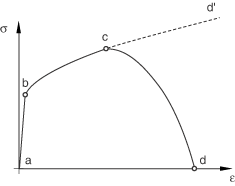
To help understand the failure modeling capabilities in Abaqus, consider the response of a typical metal specimen during a simple tensile test shown in figure 5.
Figure 5: Typical uniaxial stress-strain response of a metal specimen
The material response is initially linear elastic, a-b, followed by plastic yielding with strain hardening, b-c. Beyond point c there is a marked reduction of load-carrying capacity until rupture, c-d. The deformation during this last phase is localized in the neck region of the specimen.
Point c identifies the material state at the onset of damage, which is referred to as the damage initiation criterion. Beyond this point, the stress-strain response c-d is governed by the evolution of the degradation of the stiffness in the region of strain localization. In the context of damage mechanics can be viewed as the degraded response of the curve that the material would have followed in the absence of damage.
3.1. Ductile Damage Models Abaqus
Abaqus offers a general capability for modeling progressive damage and failure in ductile metals. The functionality can be used in conjunction with the Mises, Johnson-Cook, Hill, and Drucker-Prager plasticity models.
The capability supports the specification of one or more damage initiation criteria, including:
- Ductile
- Johnson-Cook
- Shear
- Forming Limit Diagram (FLD)
- Forming Limit Stress Diagram (FLSD)
- Marciniak-Kuczynski (M-K)
- Müschenborn-Sonne Forming Limit Diagram (MSFLD)
Figure 6: Defining ductile damage as material property in Abaqus/CAE
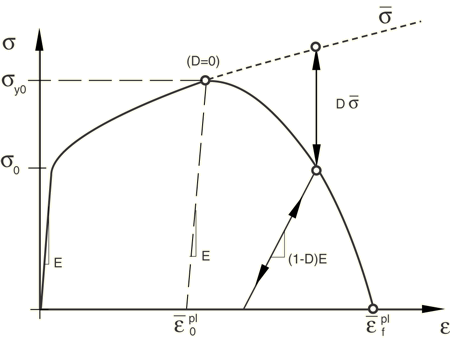
After damage initiation, the material stiffness is degraded progressively according to the specified damage evolution response (Figure 7). The progressive damage models allow for a smooth degradation of the material stiffness, which makes them suitable for both quasi-static and dynamic situations, a great advantage over the dynamic failure models. The Johnson-Cook and Marciniak-Kuczynski (M-K) damage initiation criteria are not available in Abaqus/Standard.
Figure 7: Stress-strain curve with progressive damage degradation
In figure 7, and
are the yield stress and equivalent plastic strain at the onset of damage, and
is the equivalent plastic strain at failure; that is when the overall damage variable reaches the value D=1.
Now let’s introduce these damage criteria briefly.
3.1.1. Ductile damage criterion
The Ductile damage initiation criterion is a model for predicting the onset of damage due to nucleation, growth, and coalescence of voids in ductile metals. The model assumes that the equivalent plastic strain at the onset of damage is a function of stress triaxiality and strain rate. The ductile criterion can be used in conjunction with the Mises, Johnson-Cook, Hill, and Drucker-Prager plasticity models, including the equation of state.
Stress triaxiality is defined as the ratio of pressure stress to the Mises equivalent stress.
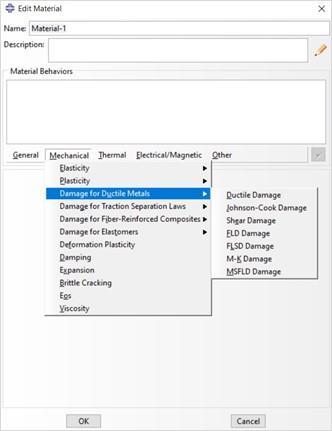
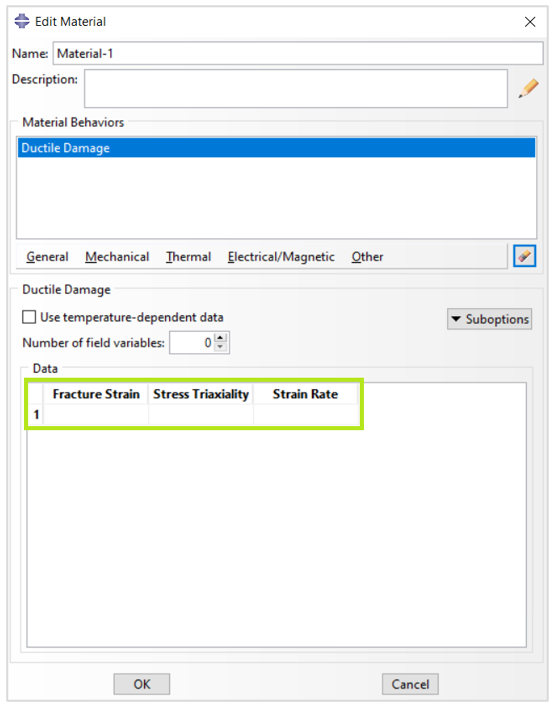
In order to define this damage criterion, you need to do as following:
“Property” Module> Create Material> Mechanical> Damage for Ductile Metals> Ductile Damage.
Then you need to provide the parameters shown in figure 4.
Figure 4: Defining Ductile damage in Abaqus
The parameters of ductile damages include:
- Fracture Strain: Equivalent fracture strain at damage initiation (Point A in figure 2)
- Stress Triaxiality
- Strain Rate: The equivalent plastic strain rate
3.1.2. Johnson-Cook damage criterion
The Johnson-Cook damage initiation criterion is a special case of the ductile damage criterion model. Other explanations are the same as ductile damage.
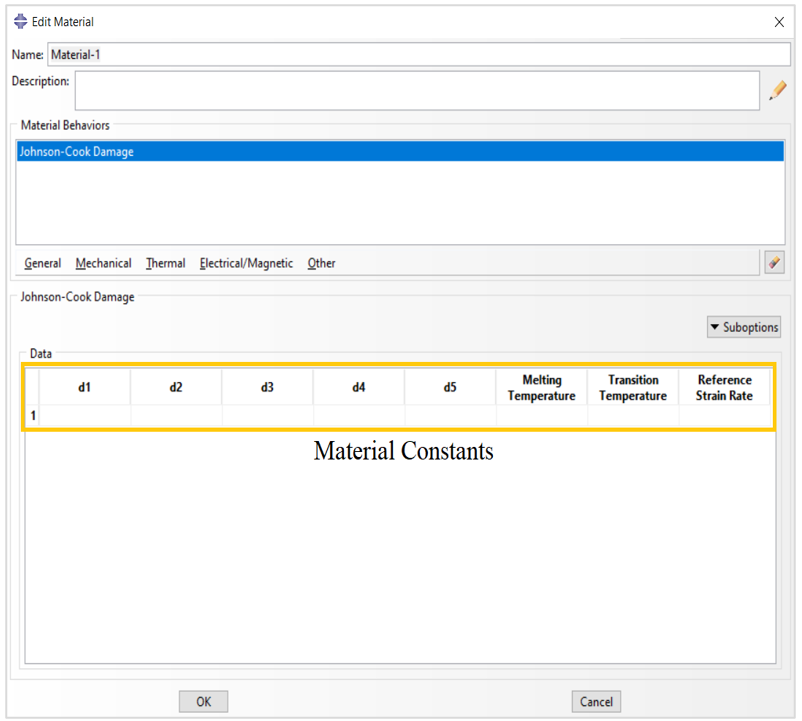
To define this damage criterion, you need to do as following:
“Property” Module> Create Material> Mechanical> Damage for Ductile Metals> Johnson-Cook Damage.
Then you need to provide the parameters shown in figure 5.
Figure 5: Defining Johnson-Cook damage in Abaqus
All of the parameters that you need to define Johnson-Cook damage are discussed in detail in the following link:
Introduction to Abaqus Johnson-Cook Model: Accurately Model High-Strain rate Events
3.1.3. Shear damage criterion
The Shear damage initiation criterion is a model for predicting the onset of damage due to shear band localization. The model assumes that the equivalent plastic strain at the onset of damage is a function of the shear stress ratio and strain rate.
The shear stress ratio is defined as:
where q is the Mises equivalent stress, p is the pressure stress, and is the maximum shear stress and
is the material constant.
To define this damage criterion, you need to do as following:
“Property” Module> Create Material> Mechanical> Damage for Ductile Metals> Shear Damage.
Then you need to provide the parameters shown in figure 6.
Figure 6: Defining Shear damage in Abaqus
The parameters of shear damages include:
- Fracture Strain: Equivalent fracture strain at damage initiation
- Shear Stress Ratio
- Strain Rate: The equivalent plastic strain rate
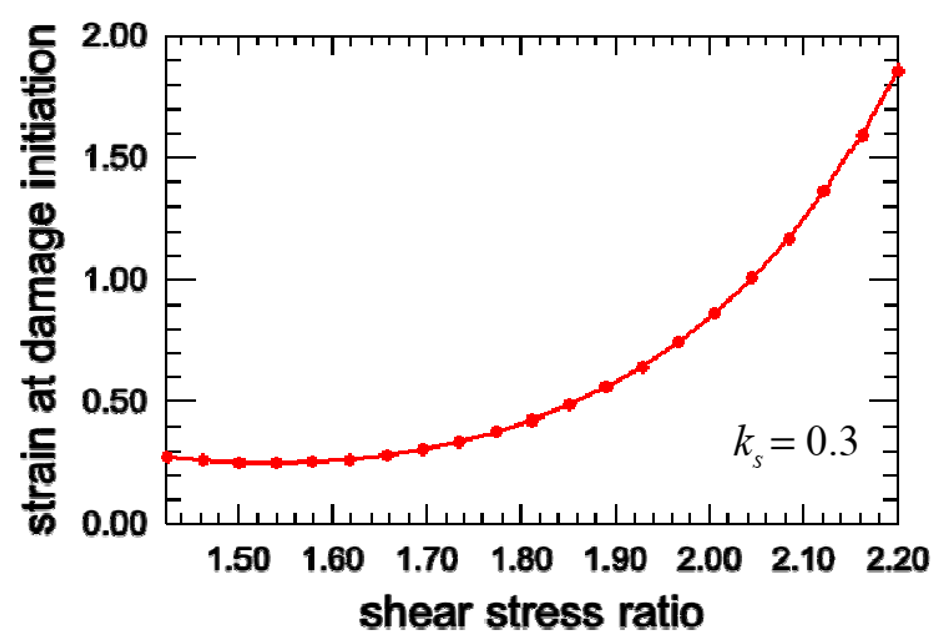
An example of strain at damage initiation versus shear stress ratio diagram is shown in figure 7.
Figure 7: Shear criterion for Aluminum Alloy AA7108.50-T6 (Courtesy of BMW)
3.1.4. Forming Limit Diagram (FLD)
A forming limit diagram (FLD) is a plot of the forming limit strains in the space of principal (in-plane) logarithmic strains.
The FLD damage initiation criterion is intended to predict the onset of necking instability in sheet metal forming. The maximum strains that a sheet material can sustain prior to the onset of necking are referred to as the forming limit strains. Damage due to bending deformation cannot be evaluated using this model.
3.1.5. Forming Limit Stress Diagram (FLSD)
The FLSD damage initiation criterion is intended to predict the onset of necking instability in sheet metal forming. The strain-based forming limit curves (as used in the FLD criterion) are converted to stress-based curves to reduce the dependence on the strain path. This improves the performance of the FLSD damage model under conditions of arbitrary loading.
Similar to the FLD criterion, damage due to bending deformation cannot be evaluated using this model.
3.1.5. Marciniak-Kuczynski (M-K)
The M-K damage initiation criterion is used to predict sheet metal forming limits for arbitrary loading paths. The model introduces thickness imperfections, in the form of grooves, in the sheet material to simulate defects. Damage occurs when the ratio of deformation in the grooves relative to deformation in the original sheet thickness exceeds a critical value. By default, Abaqus evaluates four grooves at equally spaced angles of 0°, 45°, 90°, and 135° with respect to the local 1-direction of the material at each time increment and uses the worst result to determine damage initiation. The M-K criterion can be used in conjunction with the Mises and Johnson-Cook plasticity models, including kinematic hardening.
3.1.6. Müschenborn-Sonne Forming Limit Diagram (MSFLD)
The MSFLD damage initiation criterion is used to predict sheet metal forming limits for arbitrary loading paths. The model works based on equivalent plastic strain and assumes that the forming limit curve represents the sum of the highest attainable equivalent plastic strains. The approach requires transforming the original forming limit curve (without pre-deformation effects) from the space of major versus minor strains to the space of equivalent plastic strain, , versus the ratio of principal strain rates,
.
Damage due to bending deformation cannot be evaluated using this model.
Before going toward the last part of this post, take a rest and think about what we have already learned together in this article.
3.2. Damage Evolution for Ductile Metals
The damage evolution definition defines how the material degrades after one or more damage initiation criteria are met. Multiple forms of damage evolution may act on a material at the same time—one for each damage initiation criterion that was defined.
The ductile damage criteria after initiation can follow the damage evolution by the parameters you define. They are all similar in this case. For example, for the ‘Ductile Damage’ to define the damage evolution, you need to do as follows:
“Property” Module> Create Material> Mechanical> Damage for Ductile Metals> Ductile Damage> Suboptions> Damage Evolution.
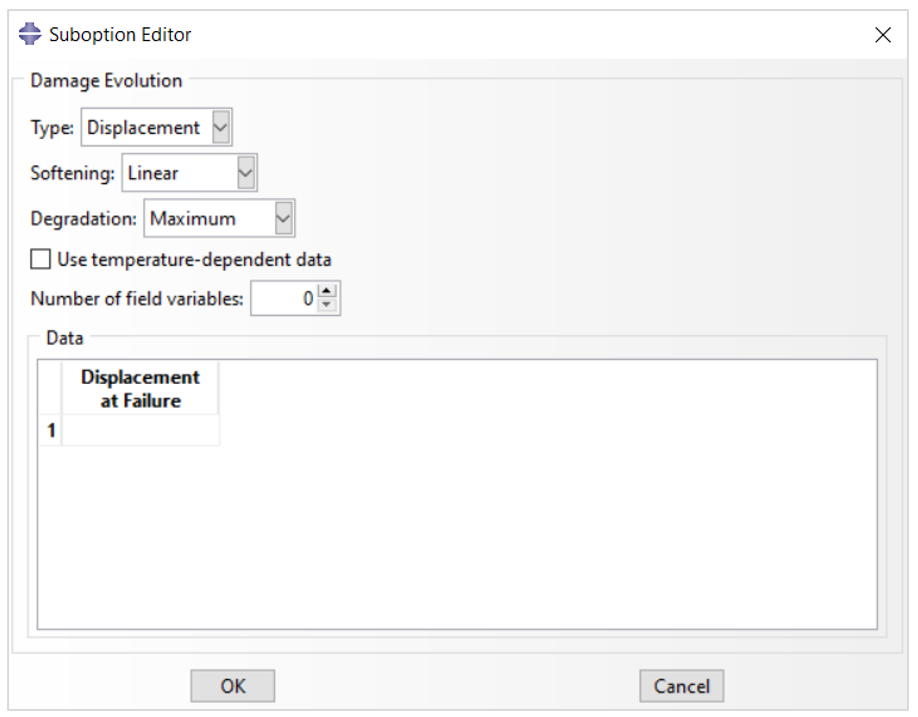
In the ‘Suboption Editor’ window, as shown in figure 8, you need to determine the parameters to define the damage evolution characteristics.
Figure 8: Determining damage evolution characteristics
The damage evolution parameters include:
- Type: This can be “Displacement” or “Energy”.
In the case of “Displacement” you need to enter the ‘Displacement at Failure’ and in the case of “Energy” you need to enter the ‘Fracture Energy’.
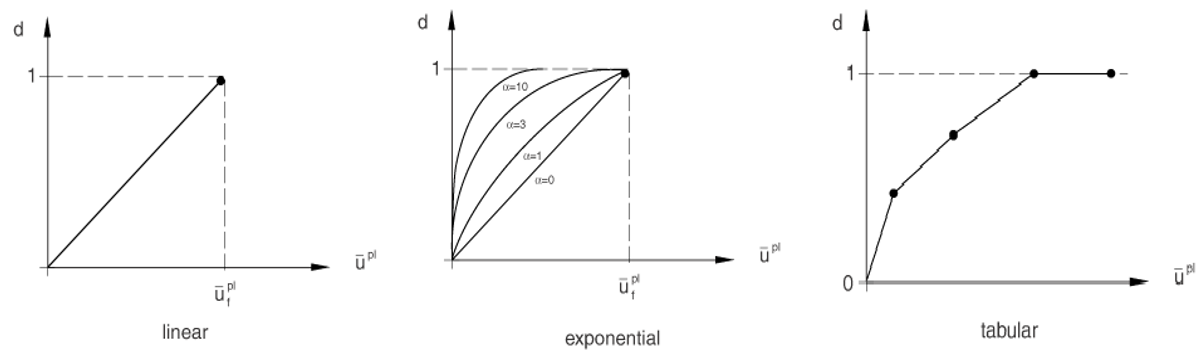
- Softening: This can be “Linear”, “Exponential” or “Tabular”.
The difference between these three models is shown in figure 9.
Figure 9: Different definitions of damage evolution based on plastic displacement
- Degradation: This can be “Multiplicative” or “Maximum”.
The overall damage variable, D, captures the combined effect of all active mechanisms and is computed in terms of individual damage variables, , for each mechanism. You can choose to combine some of the damage variables in a multiplicative sense to form an intermediate variable,
, as follows:
Then, the overall damage variable is computed as the maximum of and the remaining damage variables:
In the above expressions and
represent the sets of active mechanisms that contribute to the overall damage in a multiplicative and a maximum sense, respectively, with
.
You can also enter temperature if your model is temperature-dependent.
At this point, we reach the end of this article. Let’s summarize what we have discussed in this article.
4. How to write a Ductile Damage VUMAT?
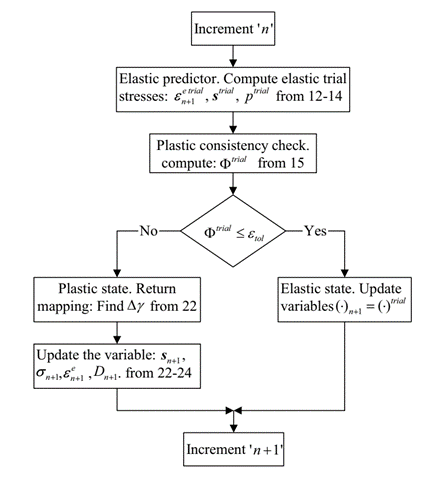
Modeling ductile damage in Abaqus VUMAT requires a constitutive model that accurately describes the damage evolution process. This section describes an algorithm for the implementation of the elastic-plastic-damage constitutive equations including the effect of crack closure. Algorithms based on the operator split concept, resulting in the standard elastic predictor/plastic corrector format, are widely used in computational plasticity. The flow chart of the elastic predictor/return mapping algorithm for the elastic-plastic-damage model is implemented as shown in figure 8 based on the article titled “Numerical analysis of damage evolution in ductile solids”.
Figure 8: Flow chart of elastic predictor/return mapping algorithm for the elastic-plastic-damage model
4.1. Ductile Damage VUMAT Subroutine
To introduce the ductile damage Abaqus model, a user material subroutine VUMAT is developed in the Abaqus software package. In the VUMAT subroutine, the damage variable will be calculated in each of the integration points (or Gauss points) locally. The element deletion option is used with VUMAT to induce ductile crack growth. The developed VUMAT subroutine has the ability to analyze ductile damage in three-dimensional and plane strain cases. 3D and 2D plane strain problems. The VUMAT subroutine is run in the Abaqus/Explicit, it can be used in various problems that require complex contact algorithms.
Using VUMAT to implement ductile damage models offers several advantages:
- Customization
Allows for the incorporation of complex damage mechanisms and user-defined material behavior.
- Versatility
Applicable to a wide range of engineering problems and materials.
- Accuracy
Provides a precise representation of damage evolution, leading to more reliable FEA results.
In order to get access to the ductile damage VUMAT subroutine in Abaqus you can see the following link:
“Ductile Damage Abaqus model for 3D continuum element (VUMAT Subroutine)“
Now let’s check how accurate and reliable our VUMAT is.
4.2. Ductile Damage VUMAT Verification
Calibrating and validating the ductile damage model implemented in VUMAT is crucial for obtaining reliable FEA results. This involves comparing the numerical predictions with experimental or physical test data.
For verification of the VUMAT, the simulation of a three-point bending test is investigated (Figure 9).
Figure 9: Comparison of experimental Giovanola et al. (1999) crack initiation site in three-point bending test with
Figure 9 (a) shows the real three-point bending test and as you can see the crack is propagated from the middle of the sample. Figure 9 (b) also shows the damage contour provided by the ductile damage VUMAT. The result is earlier damage localization and deterioration of the central region compared to the outer edges. This suggests that fracture initiation should be expected in this region. This result is in agreement with the experimental observations.
4.3. Ductile Damage VUMAT Application
After the VUMAT subroutine is verified, it can be used to predict the occurrence of damage growth and failure in various mechanical processes. For example; the modified ductile damage model is applied to predict the initiation of the micro-void as a central burst along the bar axis during the forward extrusion (Figure 10).
Figure 10: Prediction of central burst along the bar axis during the forward extrusion
5. Summary
In this article, we tried to review the ductile damage and available criteria in Abaqus. We started with the basic definition of damage in material, and then we talked about continuum damage mechanics which concerns the damage evolution inside itself. Seven ductile damage criteria in Abaqus are introduced and a ductile damage VUMAT is also provided to model ductile damage. This VUMAT is also verified with three-point bending test results and after that, it was implemented to predict the occurrence of damage growth and failure in a mechanical process such as extrusion. The results are in great agreement with the real-world data.
If you are modeling ductile damage in your projects, we highly recommend seeing the following link for more information about ductile damage modeling in Abaqus:
“Ductile Damage Abaqus model for 3D continuum element (VUMAT Subroutine)“
In the end, we appreciate for reading this article. Don’t forget to leave us your comments about this article to improve our content quality. Wish you the Best.
Read More: The meaning of specific internal energy and dissipated inelastic specific energy