Optimization in ABAQUS
In dictionaries such as Merriam-Webster optimization means “an act, process, or methodology of making something, such as a design, system, or decision as fully perfect, functional, or effective as possible.” For example, imagine an airline company doing an optimization program on its scheduling to ensure that it serves the maximum number of passengers possible. Another example on a mathematical procedure such as finding the maximum of a function. Optimization is applied in various domains and problem areas, including industrial processes, finance and investment management, communication networks, and more. Each of these domains has its own specific type of optimization.
In engineering, optimization is used to improve the design of systems and structures. The goal of optimization is to maximize performance while minimizing cost, weight, or other parameters. Optimization is important in engineering as it helps to improve efficiency, reduce costs, and increase safety.
Structural optimization
Structural optimization refers to the process of designing or modifying structures in such a way that they meet certain performance criteria while minimizing or maximizing certain objectives. It involves finding the optimal configuration, shape, or material distribution of a structure to achieve desired outcomes, such as maximizing strength, minimizing weight, reducing cost, or improving efficiency.
The goal of structural optimization is to find the most efficient and effective design for a given set of constraints and objectives. This can involve determining the optimal arrangement of structural elements, selecting appropriate materials, optimizing geometric parameters, or finding the best combination of design variables.
Structural optimization has applications in various fields, including civil engineering, aerospace engineering, mechanical engineering, and automotive design. It allows engineers to explore a wide range of design possibilities, improve the performance of structures, reduce material usage, and ultimately create more efficient and cost-effective designs.
The Abaqus software performs structural optimization within four types: Topology, Shape, Sizing, and Bead optimization. In this training package, we just explain Topology optimization and you will learn all tips and tricks about it in the lessons and workshops.
Optimization terminology in Abaqus
There are some words and concepts in the Abaqus that need to be explained because Abaqus use these words to apply and explain its functions; so, you need to understand them.
Optimization Task: It specifies the type of optimization (Topology, shape, …) and it’s the primary tool of an optimization process, which carries all other necessary settings with it.
Design area: The design area (design domain or optimization region) is the region of your model that the structural optimization modifies.
Design responses: The inputs to the optimization are called the design responses. In other words, you could say that the design responses are the goals of the optimization.
Objective Function: It is a quantity that is to be maximized or minimized. These can be single term design responses or combinations of design responses.
Constraints: They are quantities that will place bounds on the optimization problem (design responses). In other words, Constraints restrict the value of a design response.
Design variable: For an optimization problem, the design variables represent the parameters to be changed during the optimization.
Geometric restrictions: Geometric restrictions are constraints that are applied directly to the design variables. Geometric restrictions allow you to model design limitations and manufacturing limitations.
Optimization Process: It’s a process that reads an optimization task that you defined in the Optimization module and iteratively searches for an optimized solution based on the objective functions and constraints that you defined in the optimization task.
Stop conditions: With the stop conditions, you can specify when the optimization process must be finished.
Lesson 1: What is Topology optimization?
The study of topology involves examining the geometrical properties of a part or material that remain constant despite continuous changes in shape or size. For instance, when a part is twisted or bent, its underlying topological characteristics remain unchanged.
Topology optimization is a computational design methodology used to optimize the material layout within a given design space to achieve an optimal structural configuration. It aims to determine the most efficient distribution of material within a structure while satisfying specified performance criteria and constraints.
The goal of topology optimization is to find the optimal arrangement of material to achieve desired objectives, such as minimizing weight, maximizing stiffness, increasing structural strength, or improving other performance metrics. It allows engineers to explore innovative and efficient designs by removing unnecessary material or redistributing it to areas experiencing higher loads or stresses.
In this lesson, you will learn more details about the Topology optimization concept and other related things. This was just a glance of this concept.
Topology optimization algorithms
Abaqus employs two primary algorithms for topology optimization: the general algorithm and the condition-based algorithm.
General Algorithm
The general algorithm is a versatile and robust approach that can handle a wide range of topology optimization problems. It utilizes the Solid Isotropic Material with Penalization (SIMP) method, which involves assigning a density value to each element in the finite element mesh. The density represents the amount of material present in the element, with higher values indicating denser material and lower values indicating voids or empty spaces.
The general algorithm iteratively adjusts the density values of the elements based on a set of optimization objectives and constraints. The optimization objectives typically relate to maximizing stiffness, minimizing weight, or satisfying certain displacement or stress constraints. The constraints ensure that the design remains feasible and meets the design requirements.
Condition-Based Algorithm
The condition-based algorithm is a more efficient alternative to the general algorithm for certain types of problems. It is based on the concept of removing elements that exhibit high stress or low stiffness during a preliminary analysis. This approach can significantly reduce the computational cost of the optimization process, especially for large-scale problems.
However, the condition-based algorithm has limitations compared to the general algorithm. It is less flexible and may not be able to find the optimal solution for all types of problems. Additionally, it may produce designs with discontinuities in the density distribution.
These two algorithms will be completely explained in this lesson and you will understand the difference between them.
Lesson 2: Topology Optimization with General (Sensitivity-based) algorithm
In this lesson, all settings that need to be done to apply a Topology optimization in Abaqus with General algorithm, such as optimization task and Desing responses will be explained in details.
To do a Topology optimization with the General algorithm, First, you must create an optimization task for the topology and in the settings window select the General algorithm and do other required settings, which will be explained in the lesson. Next, the design responses must be set. The design responses could be single term design response or a combination of several design responses. The General algorithm supports some of the design responses that may be not available in the other algorithm. After that, you must decide which of these design responses must be used as the objective functions or the constraints. How to decide this or how to apply each one, all will be explained in this lesson.
Because sometimes the topology optimization may lead to a model that is challenging to manufacture. Therefore, the optimization module provides some additional constraints called “Geometric Restrictions” to solve this issue. Therefore, after applying all the previous settings, you must apply the necessary Geometric Restrictions to have a model that could be easily manufactured.
Lesson 3: Topology Optimization with Condition-based algorithm
All the steps explained in the previous lesson must be taken too to do a Topology optimization with the Condition-based algorithm. However, they are different in detail. For example, the settings in the Optimization Task, types of design responses, calculation methods, and some other things. Each one will be explained completely with simple examples to better understand this algorithm the its difference with the General algorithm.
Lesson 4: What is an Optimization process?
In this lesson you will learn what is an Optimization process, how it’s done, how to apply an optimization process, the files generated by it, and some tips about post processing will be mentioned.
The optimization process iteratively updates the design variables, modifies the finite element model, and runs Abaqus analyses while it searches for an optimized solution. To create an Optimization Process, you must go to the Job module and use the last tool you see in the toolbox area.
When an optimization process is running, two types of data will be generated: the Abaqus analysis results and the optimization results. Each type generates its related files. The Abaqus analysis results generate “dat”, “message”, “status”, “inp”, and “odb” files. All of these files will be saved in the working directory path. The optimization results generate the optimization variables files, which have the extension “onf”; these are the outputs generated automatically by the optimization module and will be appended to the output database file as field data, which you can see as plot contours in the visualization module.
Two types of data will be generated during the optimization process; the analysis and optimization results. So, to be able to see the results in the visualization module, you must combine these two into a single results output database file.
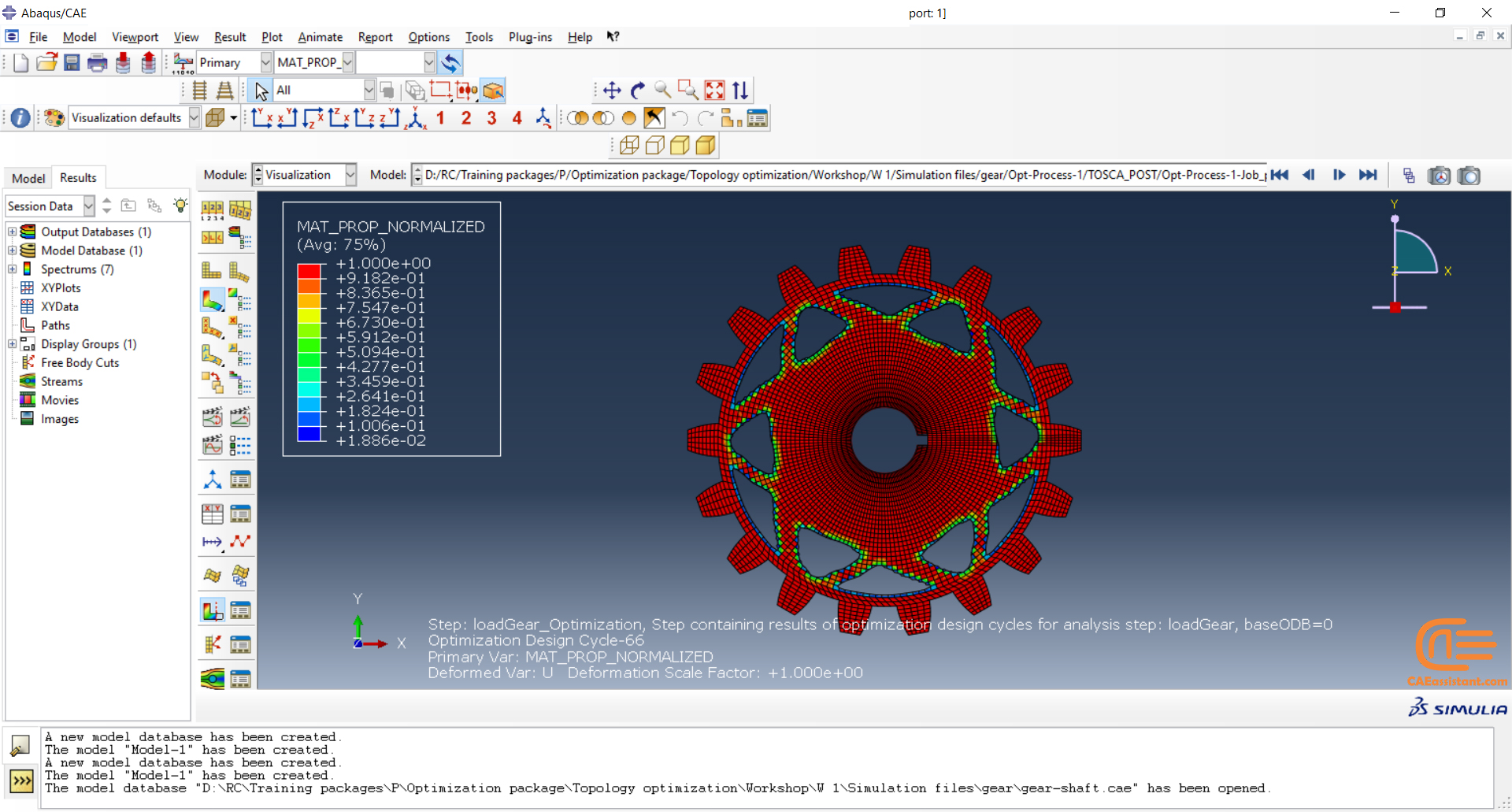
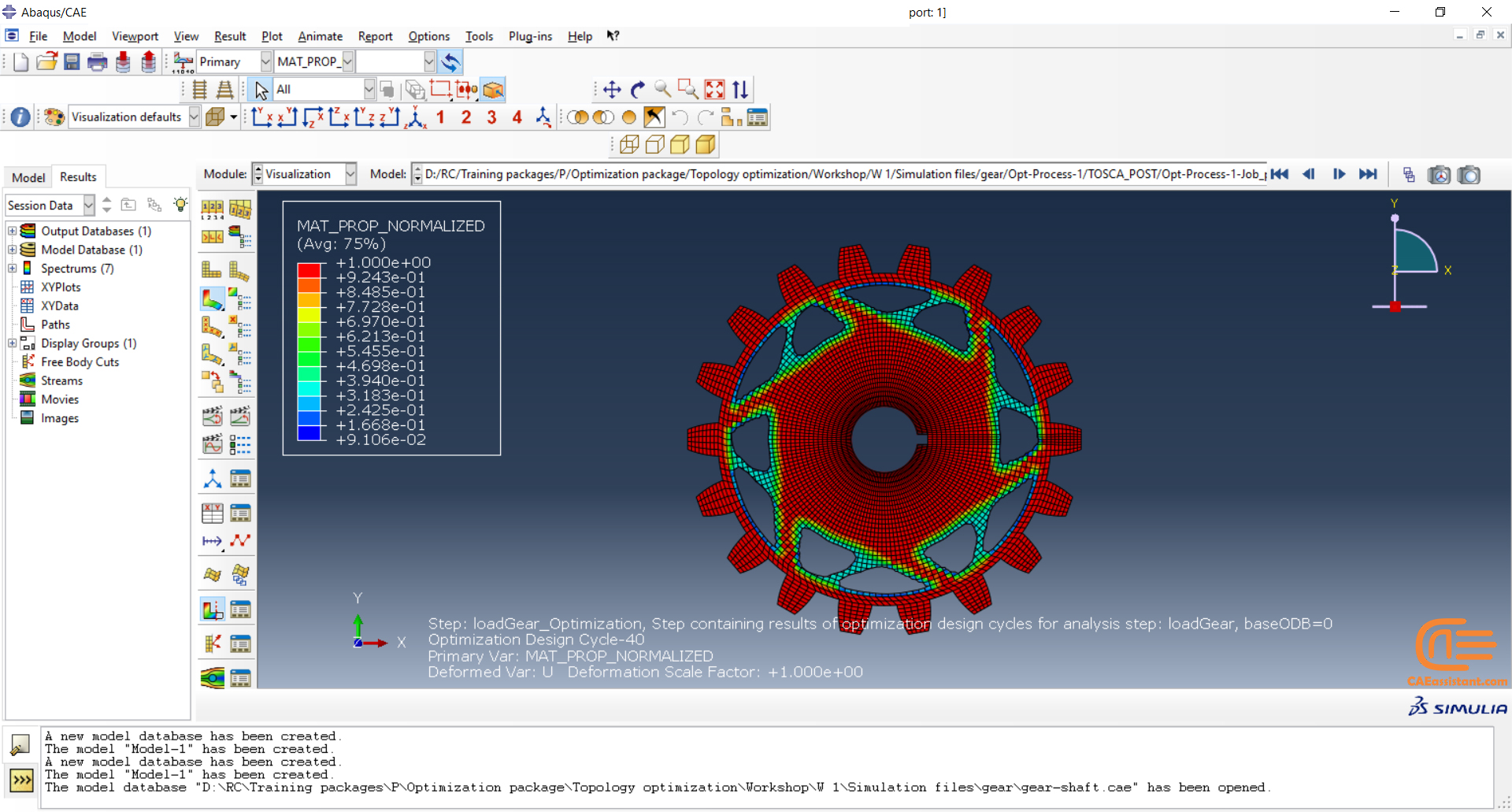
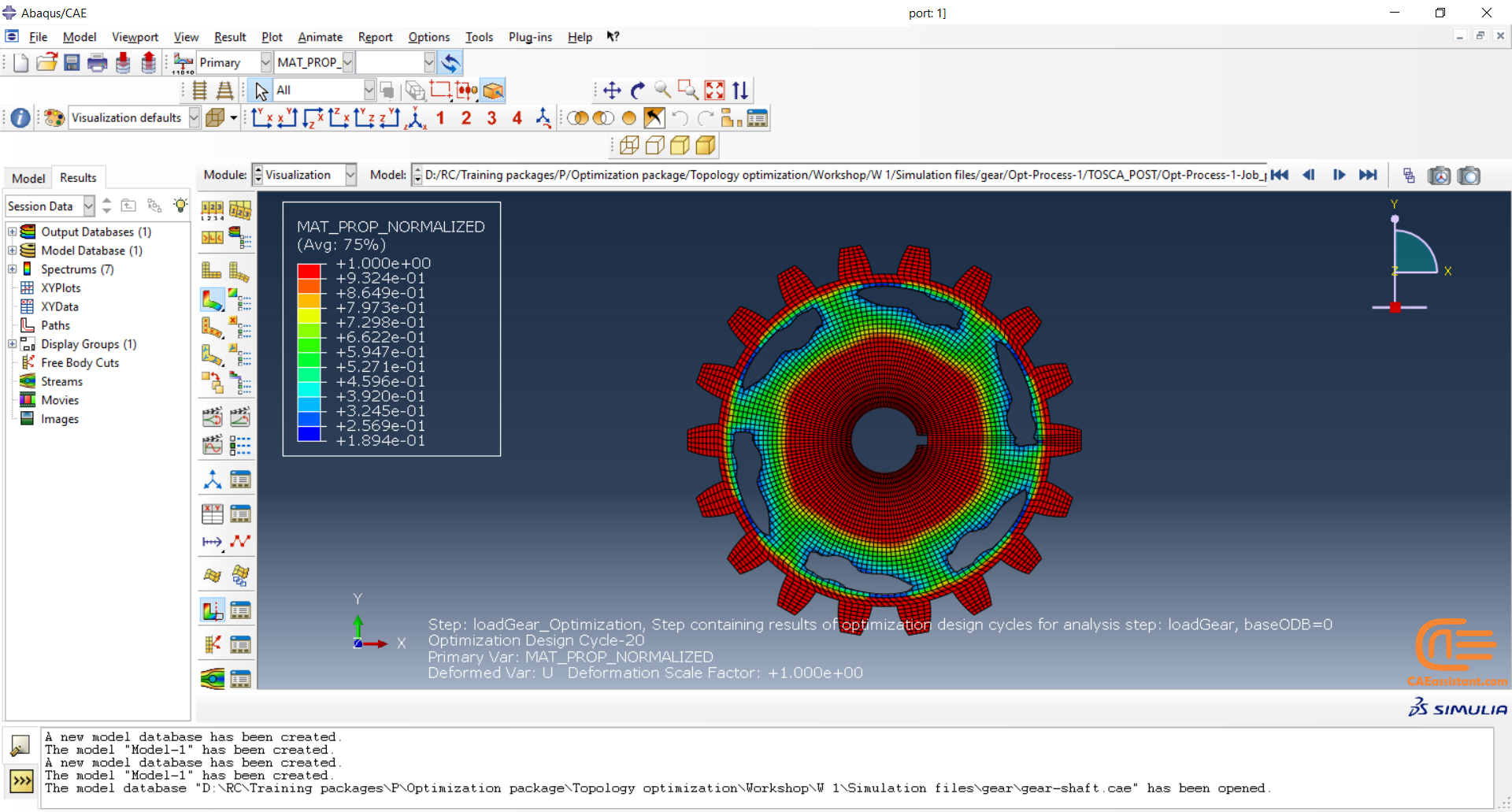
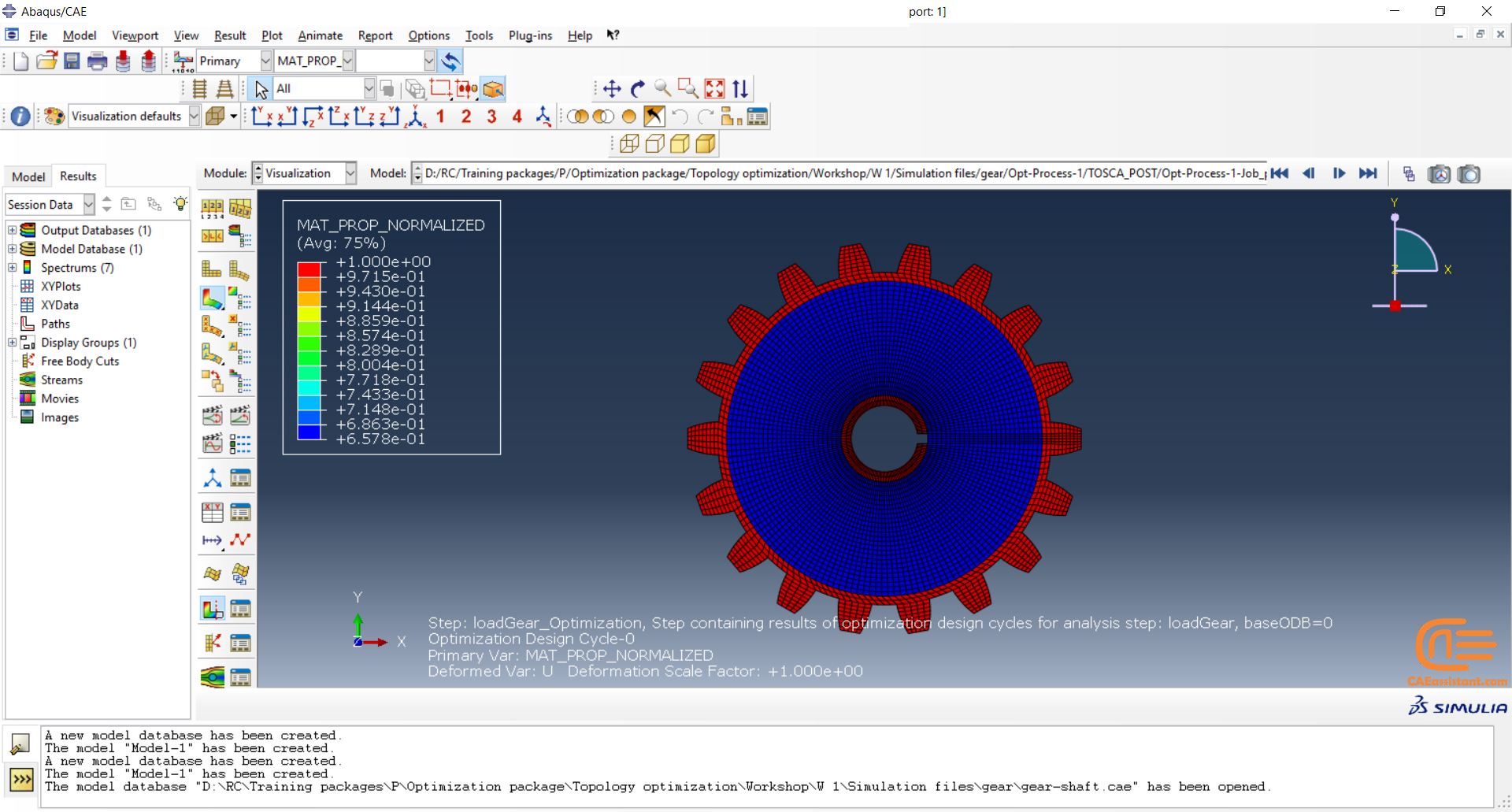
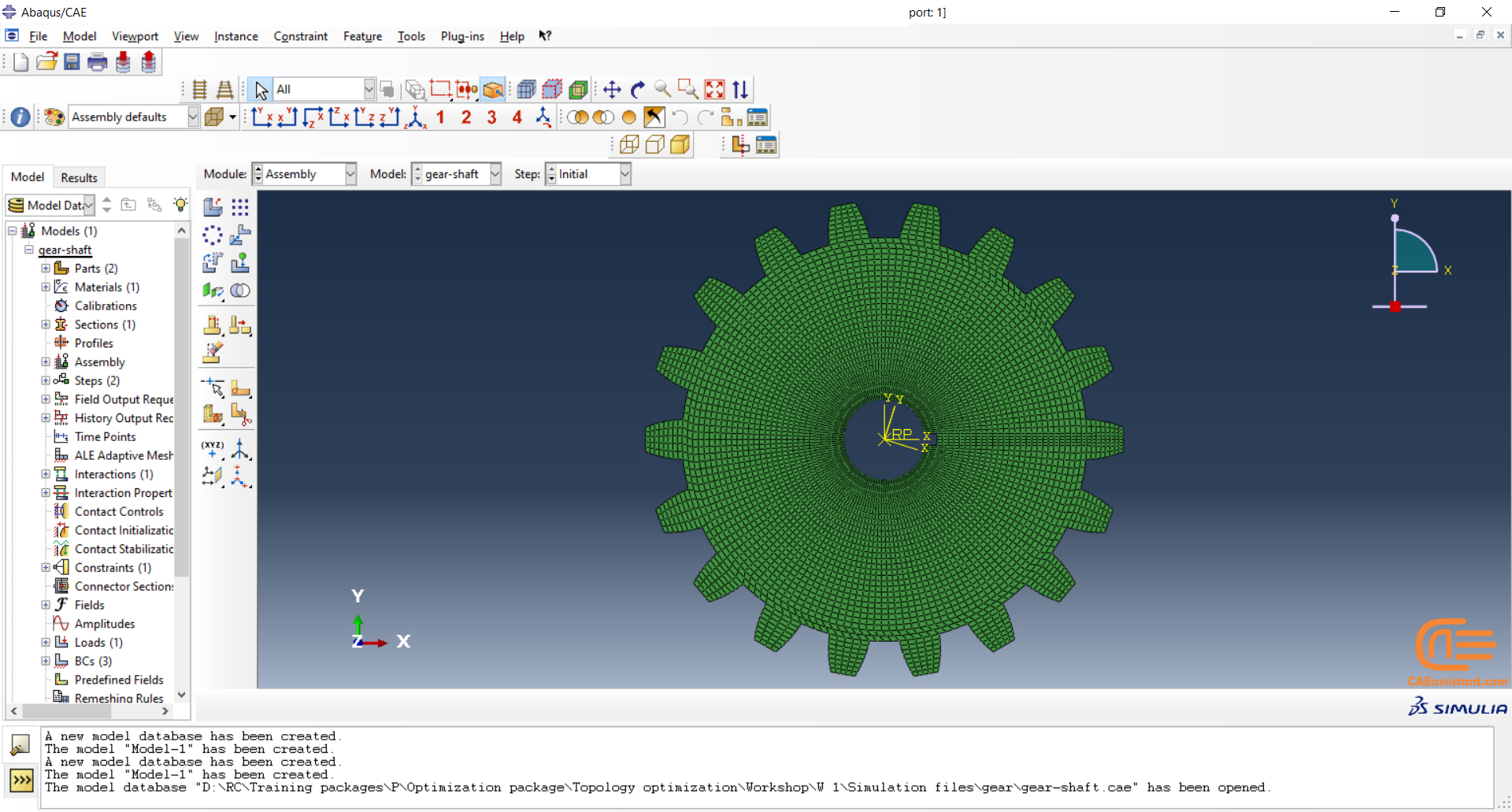
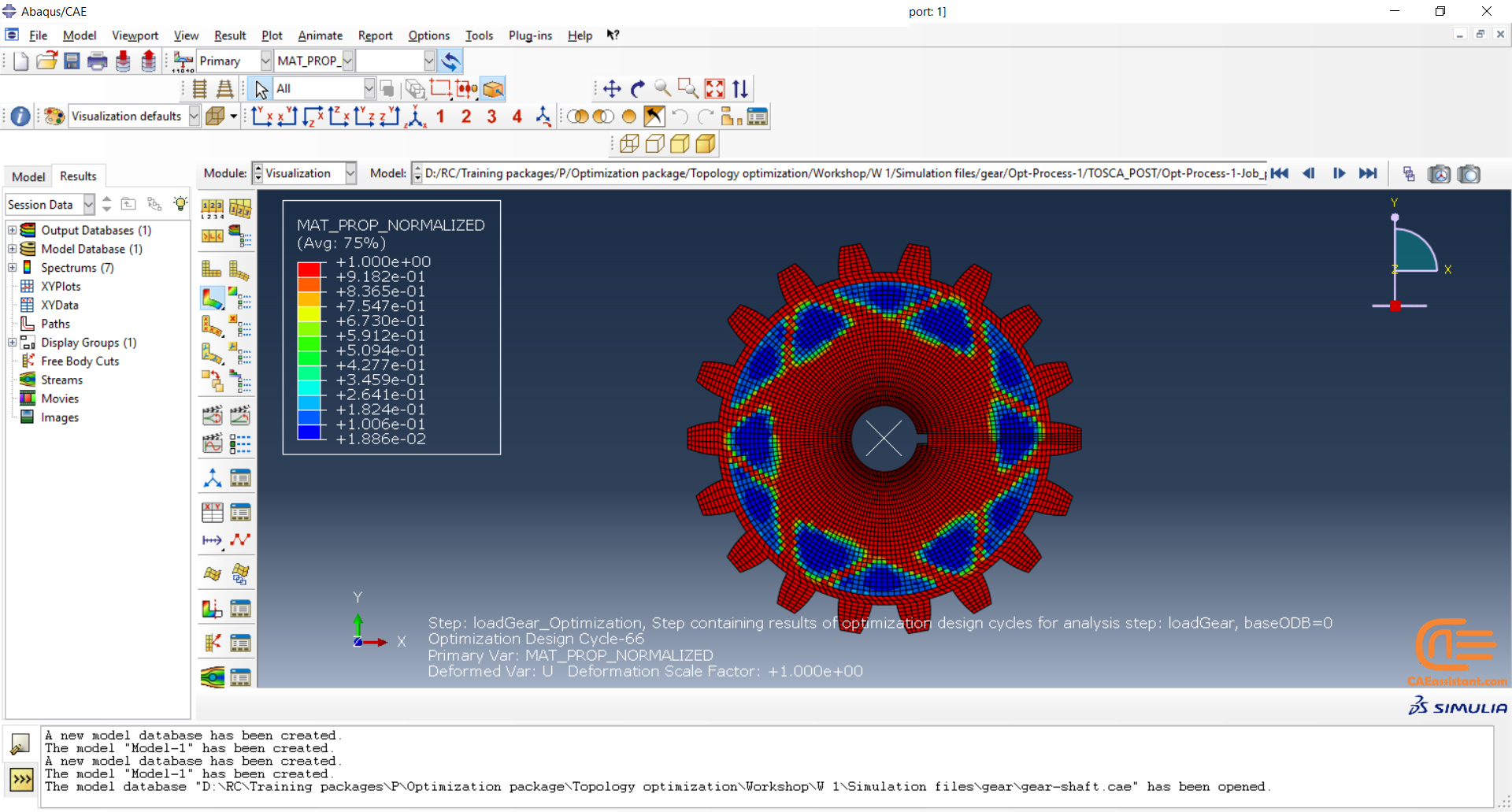
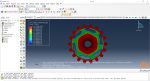
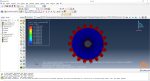
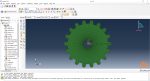
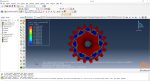
Workshop: Topology optimization of a gear with general algorithm
The model we want to optimize in this workshop is a 2D gear/shaft assembly. In this workshop, you will set up an optimization task that will use the sensitivity-based (General) algorithm. We are pursuing three goals in this optimization. To maximize the stiffness of the gear while reducing the mass of the gear by 25% and the moment of inertia of the gear/shaft assembly by 10%. Furthermore, geometric restrictions for symmetry and frozen areas will also be created.
All the detail and results analysis is presented in this workshop.
It would be helpful to see Abaqus Documentation to understand how it would be hard to start an Abaqus simulation without any Abaqus tutorial. Also, be careful with the units of values you insert in Abaqus. Yes! Abaqus don’t have units but the values you enter must have consistent units. You can learn more about the system of units in Abaqus.













Chlebek –
The lessons cover the basics of topology optimization, including terminology, algorithms and the optimization process. The workshop is a valuable addition, allowing learners to apply their knowledge to a practical example . However, it would be beneficial to include more diverse examples from different engineering domains.
Gang –
The tutorial videos are satisfying and the step-by-step procedures are easy to follow. It would be better if more workshops are provided in the package.
Experts Of CAE Assistant Group –
Thanks. In the production plan, the production of more workshops is on the agenda