Introduction | Shape Control Piezoelectric Abaqus
This training package provides comprehensive information on piezoelectricity, its reversible nature, and how it allows for the accumulation of electric charge in certain solid materials under mechanical pressure. Some materials exhibit direct piezoelectricity, generating electric charge internally through mechanical force, while others display the inverse piezoelectric effect.
By effectively utilizing piezoelectric properties, it becomes feasible to manipulate the shape of objects in response to external forces. However, it is important to consider the cost-effectiveness of employing this property in all scenarios. Consequently, it is more practical to selectively incorporate piezoelectric structures, particularly in specialized applications.
One approach to determining the ideal placement of piezoelectric elements for controlling the shape of various objects, both internally and externally, involves the utilization of the Abaqus and MATLAB software linkage. This combination, together with optimization algorithms like the bird optimization algorithm, enables the achievement of desired objectives.
Through the utilization of these tools and the associated data, the primary objective of object shape control can be successfully attained. This training package will cover topics such as piezoelectricity and piezoelectric modeling in Abaqus, the bird optimization algorithm, the integration of Abaqus and MATLAB, and practical applications of these tools for shape control.
Lesson 1: Introduction to Piezoelectric
Piezoelectricity or high-pressure effect, so to speak, refers to a special feature that exists in some crystalline materials, special ceramics and biological materials such as bone, DNA strands (deoxyribonucleic acid) and various proteins. Based on this property, this group of materials produces electric charge against mechanical stress. In fact, the term “piezoelectric” refers to the production of electric current due to the application of mechanical force. In many scientific texts and articles, the piezoelectric effect has been introduced as an electromechanical exchange between electrical and mechanical states in crystalline materials. In such a way that there is a reversible relationship between these two; that is, as a result of applying mechanical force to a piezoelectric material, an electric charge is produced, or as a result of producing an electric charge in it, the desired material is stretched or compressed.
In a crystalline material such as lead zirconate titanate, piezoelectric properties appear when the crystal structure of this material changes by about 0.1% compared to its initial state and dimensions. This property is also called direct piezoelectric effect in some texts. Another effect that is important and worthy of attention in the discussion of piezoelectric materials is called the inverse piezoelectric effect; An effect based on which, when an electric current is applied to a piezoelectric material, the material changes its shape. Today, this feature is used to produce ultrasound waves.
Mechanism and operation of piezoelectrics
The piezoelectric effect is associated with the creation of an electric dipole moment in solids. This phenomenon can occur due to the induction of ions around the crystal lattice, resulting in an asymmetric charge environment, or it can be directly transferred by molecular groups. The dipole density for crystals can be easily calculated by summing the electric dipole moments of each volume in the crystallographic unit cell. Since every dipole is a vector, the dipole density (p) is a vector field. Close dipoles tend to align in areas known as Weiss domains. While these domains are typically randomly distributed, they can be aligned through polarization processes. It is important to note that not all piezoelectric materials can be polarized.
One significant aspect of the piezoelectric effect is the change in polarization (p) when a specific mechanical force is applied. This change can be caused by the reconfiguration of the dipole induction environment or by the rearrangement of molecular dipole moments under the influence of mechanical force. Generally, the piezoelectric property can occur as a result of changes in the dipole configuration within the crystal lattice, the symmetry of the crystals, or the application of mechanical force from the surroundings. It appears that the change in the polarization dipole corresponds to a change in the surface charge density on the crystal plane. In other words, it represents an electric field change that occurs between the planes or surfaces due to a change in the dipole density within the volume. For instance, applying a force equal to 2 kilonewtons to one cubic centimeter of quartz can generate a potential difference of 12,500 volts.
Lesson 2: Optimization algorithms and particle swarm optimization algorithm
Optimization algorithms
The goal of optimization algorithms or heuristic algorithms is to provide a solution within an acceptable time frame that is suitable for solving the problem, the heuristic algorithm may not be the best real solution for solving the problem, but it can be a solution close to the best. Heuristic algorithms can be combined with optimization algorithms to improve the efficiency of the algorithm. The meta-heuristic algorithm is a combination of heuristic algorithms that are designed to find, generate, or select any heuristic at each step and provide a good solution to problems that are optimization problems. Meta-heuristic algorithms consider some assumptions of optimization problems to be solved.
Particle Swarm Optimization (PSO) algorithm
The Particle Swarm Optimization (PSO) algorithm is a social search algorithm inspired by the collective behavior of bird flocks. Initially, this algorithm was developed to understand the patterns governing the synchronized flight of birds, their sudden changes in direction, and the optimization of their flock’s shape. In PSO, particles traverse the search space, and their movement is influenced by their own experiences and the knowledge of their neighbors. Therefore, the positions of neighboring particles impact how an individual particle explores the search space, resulting in a search process where particles tend to converge towards successful areas. Through the exchange of knowledge, particles learn from each other and move towards their best-performing neighbors.
The algorithm operates on the principle that, at any given moment, each particle adjusts its position in the search space based on its own best-known location thus far and the best-known location within its entire neighborhood.
Collective intelligence and neural network
Collective intelligence is a systematic feature that in this system, particles (agents) cooperate with each other locally and the collective behavior of all agents causes a convergence at a point close to the global optimal solution. The strength of this algorithm is the lack of a global control. Each particle (agent) in this algorithm has relative autonomy that can move throughout the solution space and must cooperate with other particles. Two famous collective intelligence algorithms are ant colony optimization and particle swarm optimization. Both of these algorithms can be used to train neural networks. Artificial neural networks have many features such as adaptability, learnability and generalization. In the field of pattern matching, artificial neural networks are able to classify new patterns into related classes based on their previous learning. Using the new idea of collective intelligence in combination with artificial neural networks is a solution to overcome the challenge in neural networks.
The mechanism and operation of the particle optimization algorithm
A group of birds is randomly searching for food in a given space. Within the space, there is only one piece of food. None of the birds know the location of the food, and one of the best strategies is to follow the bird that is closest to the food. This strategy forms the basis of the algorithm, where each solution that leads the birds to the food is referred to as a particle. Every particle in the algorithm has a merit value, which is calculated using a merit function. The merit value of a particle increases as it gets closer to the target (representing the food in the bird movement model) in the search space. Additionally, each particle possesses a speed that determines its movement. By following the optimal particles in the current state, each particle continues its movement in the problem space.
The algorithm begins by randomly generating a group of particles, and through successive generations, they attempt to find the optimal solution. In each step, every particle is updated using the best value achieved so far. The best position attained by a particle, which is recognized and maintained, is referred to as the “pbest”. The algorithm also utilizes another best value, known as the “gbest”, representing the best position obtained thus far by the entire population of particles. After identifying the best values, the speed and location of each particle are updated using equations (1) and (2).
Lesson 3: Linking Abaqus and MATLAB
Mechanical engineers utilize Abaqus, an analytical software, for modeling purposes. This software offers a wide range of capabilities, making it possible to easily model even the most complex problems. In most modeling scenarios, including those involving high degrees of non-linearity, users only need to specify engineering data such as the problem’s geometry, material behavior, boundary conditions, and loading method. Additionally, programming software can be employed for various analyses and optimizations related to loading patterns. In this research, MATLAB programming software is utilized to achieve the research objectives. MATLAB is chosen due to its high-level programming language, as well as its convenient matrix operations, calculations, and functions that incorporate different algorithms.
In many research endeavors, it is often necessary to have software that offers the analysis capabilities of Abaqus while also being as user-friendly and powerful as MATLAB for programming tasks. Fortunately, by linking these two software tools, users can fully leverage the strengths of each and make use of their combined features. This linking feature enables researchers to attain their desired goals and transfer data obtained from algorithms to Abaqus for obtaining the desired results.
How to link Abaqus and MATLAB software
In order to connect two software to analyze the appropriate model, the model must first be modeled in Abaqus software and after obtaining the answer, receive a text response from it. Then, in MATLAB software, we type the link command of two software and specify the location of the answer in the system.
Workshop: Optimizing the placement location of piezoelectrics to control sheet lift by bird optimization algorithm
To control the shape of the desired model, lead zirconate titanate (PZT-4) piezoelectric materials have been utilized. These materials possess specific inherent properties that are incorporated into the corresponding sections of the Abaqus software. After introducing the materials used and the piezoelectric components in the model, twenty pairs of piezoelectrics were placed on the vertical face and ten pairs on the horizontal face. Careful attention was given to the placement, ensuring a one-millimeter distance from the bottom of the model for the vertical face and a one-millimeter distance from the model’s head for the horizontal face. Once the piezoelectrics were arranged, the solution conditions were introduced to the Abaqus software through a static command. The installation state and mode of the piezoelectrics on the model were specified. The forces acting on the model, including gravity, support conditions, and currents connected to each piezoelectric, were defined. The current flow to each piezoelectric was set such that the surfaces facing the model had a positive current, while the opposite surfaces had a negative current. However, the optimization algorithm could alter this configuration by selecting negative currents for each piezoelectric pair.
The MATLAB software, coupled with the particle swarm optimization algorithm, facilitated the application of algorithm data to Abaqus and the retrieval of model status and variable information. The algorithm involved creating a matrix representing the voltage applied to each piezoelectric pair connected to the model. The algorithm randomly assigned values to each matrix data (bird) based on the current input. Subsequently, this matrix was applied to Abaqus to determine the voltage of each piezoelectric pair. Abaqus played a crucial role in defining the objective function by considering the strain on the model’s head and the total current applied to the piezoelectrics as response factors.
The MATLAB software facilitated the creation of a new file that encompassed the algorithm and all the relevant conditions, such as the number of birds (variables or piezoelectrics), the range of variable changes, the algorithm termination criteria, formula writing, coefficient introduction, and objective function specification. The coefficients C1 and C2, representing the influence of local and global situations, respectively, were set to two, based on available resources. The inertia coefficient (w) was assigned a value of 0.99 to promote optimal solutions and minimize the objective function.
To determine the objective function’s output in the bird algorithm program, a separate window was created, linking the two software tools and transferring the answer to the optimization algorithm. This process involved modifying the model by altering the flow of piezoelectrics, transferring the changes to Abaqus, and retrieving the desired response (model head deformation and total current). The final objective function answer was determined by summing the absolute values of the current for each piezoelectric pair and multiplying the strain on the model’s head by ten million.
The coefficient assigned to the model head strain aimed to balance the two introduced values and improve the analysis process. Without considering an appropriate coefficient, the algorithm would reduce the currents without reducing the model head strain. Conversely, if a coefficient favoring the model strain over the current totals was chosen, the algorithm would prioritize strain reduction, neglecting other objectives. The selected coefficient was the closest approximation to achieve the desired outcome.
Using the MATLAB files, the desired parameters (current applied to each piezoelectric pair) were modified, and the updated file was executed in Abaqus to obtain new results. The algorithm identified the bird closest to the final answer (with the lowest sum of current and strain) as the target bird and adjusted the speed and position of other birds accordingly. This process was repeated, with the best position among all steps serving as the new target. The algorithm continued until the strain on the model’s head reached zero or fell below specific thresholds, at which point the optimization process ceased, and the voltage values of the obtained piezoelectrics were considered the final solution for that stage.
In subsequent steps, piezoelectric currents lower than two-tenths of the maximum voltage introduced to the algorithm were set to zero, reducing both strain and the number of piezoelectrics used. The optimization process aimed to find the optimal solution with fewer variables. The process continued until the currents controlling the model’s shape approached the maximum voltage, or when the dimensionless state of all currents exceeded eight-tenths of the maximum flow. In this case, the obtained currents were considered the final answer.
It would be helpful to see Abaqus Documentation to understand how it would be hard to start an Abaqus simulation without any Abaqus tutorial. Moreover, if you need to get some info about the FEM, visit this article: “Introduction to Finite Element Method | Finite Element Analysis”. You don’t know which Abaqus software editions are suitable for you, Do not worry! This article would give you info about Abaqus editions: “How to download Abaqus? | Abaqus student & commercial edition” .




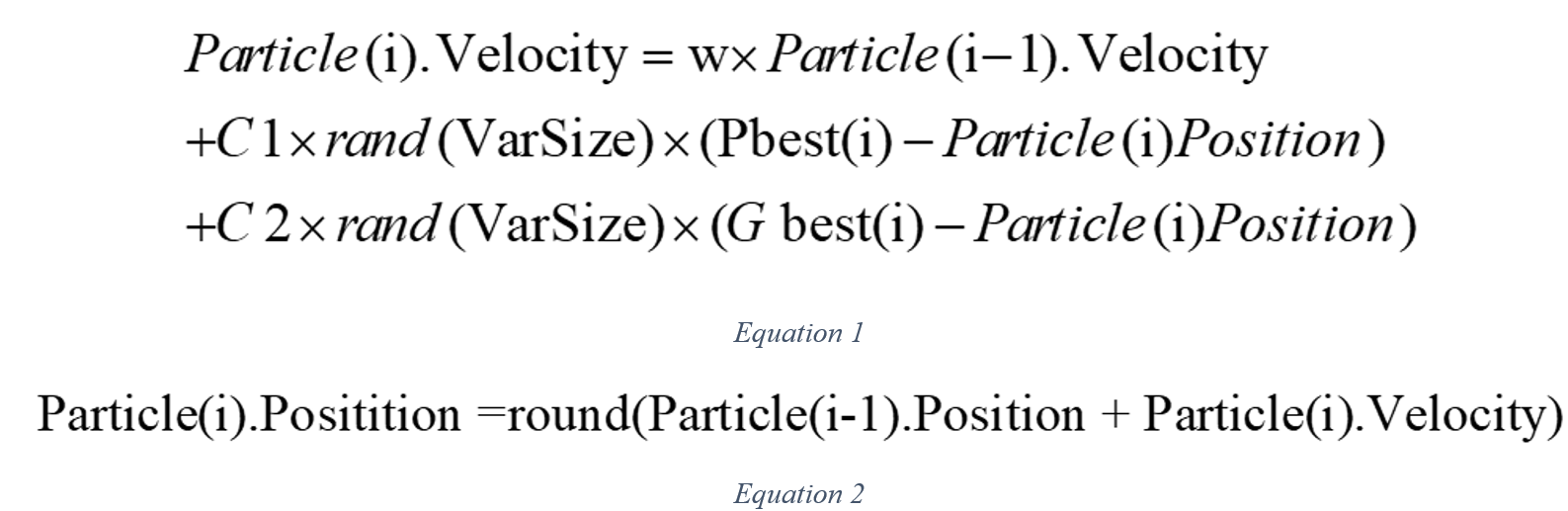


Mohan –
The simulation package for shape control using piezoelectricity in Abaqus is excellent. It provides a clear explanation of piezoelectric concepts and comprehensive training on modeling techniques in Abaqus. The inclusion of Particle Swarm Optimization algorithm for optimization and the efficient integration between Abaqus and MATLAB are highly beneficial. Overall, this product effectively addresses the objectives of shape control and comes highly recommended